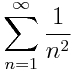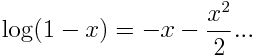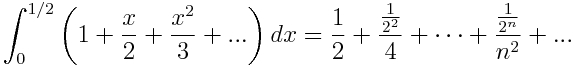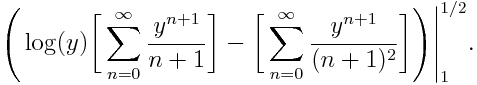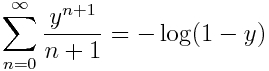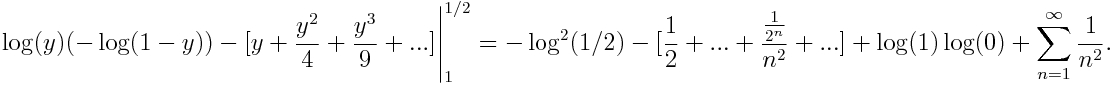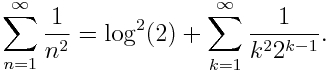En la tragedia de Shakespeare Otelo, el homónimo protagonista, general de la república de Venecia, se enamora de Desdémona, hija de un senador. Después de casarse en secreto, uno de sus alféreces, Yago, movido por el odio que siente hacia él le hace creer que su esposa es infiel con Casio, su más leal teniente. Podrido de celos, Otelo mata a Desdémona y, después de saber que todo ha sido un engaño, se suicida.

Alexander Pushkin, considerado unánimemente padre de la literatura rusa moderna, poeta consagrado, mujeriego desenfrenado, endeudado crónico, adicto al juego, odiado por la aristocracia a la que pertenecía por nacimiento pero no por ideología, contrajo matrimonio en 1831 con la bella Natalia Goncharova. Georges d’Antès, un militar francés emigrado a Rusia y casado con una cuñada de Pushkin, comenzó a asediar a Natalia, encendiendo unos irrefrenables y paradójicos celos en su libertino marido. El escritor ruso retó al oficial francés a duelo, siendo herido de muerte a las afueras de San Petesburgo la madrugada del 29 de enero de 1837.

Estos son dos célebres ejemplos de lo que un hombre despechado, tanto en el mundo real como en el de la ficción, puede llegar a hacer presa de un galopante ataque de cuernos. Los hombres de ciencia tampoco son inmunes a los celos. Ni siquiera a los celos ficticios, lo que ha dado lugar a una de las leyendas urbanas más extrañas de la historia de la ciencia y de sus más famosos premios.

Alfred Nobel fue un ingeniero e inventor sueco, nacido en una familia de profesionales del gremio. Emigrados a Rusia, Alfred, junto a sus hermanos, recibió una cuidadosa educación tanto en ciencias naturales como en humanidades. De regreso a Suecia tras la quiebra de la fábrica de explosivos que su padre había instalado en San Petesburgo, completó sus investigaciones en el campo de los explosivos, lo que dio lugar al descubrimiento de la dinamita. El hallazgo le reportó una gran fortuna y, a la vez, un gigantesco dolor moral: si bien la dinamita facilitaba la vida en algunos aspectos, también acababa con ella en los campos de batalla. Cerca de su muerte fundó la sociedad filantrópica Nobel, a la que legó la mayor parte de su fortuna y que quedó encargada de, cada año, premiar a quienes más notoriamente hubieran aportado a la humanidad en las áreas de Física, Química, Medicina, Literatura y paz mundial: habían nacido los prestigiosos premios Nobel. ¿Quedó algo de herencia para su esposa? Debemos decir que no puesto que, a pesar de que Alfred Nobel tuvo varias amantes y amores a lo largo de su vida (la condesa austro-bohemia Bertha Kinsky, la austriaca Sofie Hess…), jamás se casó. Aquí tenemos uno de los ingredientes de la posterior maledicencia.
Si nos fijamos en la lista de las disciplinas que Alfred Nobel consideró dignas de ser premiadas vemos que las Matemáticas están ausentes. ¿Por qué no existe el premio Nobel de Matemáticas? La leyenda dice que cuando Alfred Nobel pidió consejo a especialistas para saber quién merecería cada uno de los galardones, éstos le dijeron que el candidato ideal en la categoría sería el matemático sueco Gösta Mittag-Leffer, quien, según las malas lenguas mantenía un romance secreto con su esposa. ¡¡Imposible!! La rivalidad entre Nobel y Mittag-Leffer, tanto en la vida civil como en la amorosa, es un extraño producto de los agujeros en los conductos de la información: al parecer apenas se conocían el uno al otro.

El verdadero motivo por el no existe el premio Nobel de Matemáticas es que su fundador, a la hora de idearlos, no consideró esta disciplina relevante para la sociedad en un sentido práctico (lo que, ha quedado bastante patente a lo largo de la historia, es completamente falso), esa sociedad a la que, según su conciencia, tanto daño había hecho con su explosivo invento.

A pesar de la notoria ausencia, los premios Nobel no están vetados para los matemáticos. Ejemplos son el norteamericano John Nash, que recibió el de Economía en 1994 por sus trabajos en el estudio del equilibrio en la teoría de juegos no cooperativos, y el español José Echegaray, que recibió en 1904 el de Literatura por su obra dramática.

Pero si de galardonar se trata, las ciencias matemáticas no se quedan atrás. El vacío dejado por el inventor sueco rápidamente fue llenado por la Unión Matemática Internacional, que cada cuatro años otorga la prestigiosísima medalla Fields a matemáticos que hayan logrado su descubrimiento cumbre por debajo de los cuarenta años. En la lista de galardonados está la mayoría las más grandes luminarias en Matemáticas del siglo XX (y ya parte del XXI). Por otro lado nos encontramos con el premio Wolf, que se concede anualmente desde 1978 en Israel a científicos y artistas por sus logros en interés de la humanidad y de las relaciones fraternas entre los pueblos, sin distinción de raza, color, religión, sexo o tendencias políticas. El grado de brillantez de los premiados en la categoría de Matemáticas no es menor que en la Fields, apareciendo, además, aquellos que no fueron tan precoces o que lograron su descubrimiento en el umbral de los cuarenta años, como ocurrió con Andrew Wiles y su prueba del último teorema de Fermat. Finalmente, los matemáticos también optan al premio Abel, otorgado anualmente por el rey de Noruega desde 2002 en claro paralelismo con el premio Nobel.
–Nota: Esta entrada la ha escrito Fernando Jiménez. Y es que si tenemos buenos compañeros de trabajo, habrá que aprovecharlos ¿no?
y las finanzas, que es otro tema que está muy de moda con esto de la crisis económica.
euros que invertimos de nuevo y obtenemos, tras comernos las uvas
. Ahora supongamos que dividimos el tiempo tanto como queramos y vamos invirtiendo de nuevo lo que obtenemos, entonces, nuestra inversión se calcula como
y se aproxima a 2,7182. ¿Os suena éste número o la expresión? Pues debería, ¡es el límite que define el número e que se estudia en bachiller! (al menos yo lo hice…)