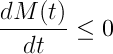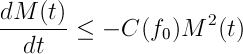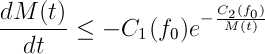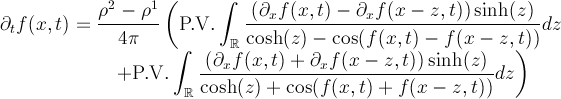Tag Archives: física

Problemas de frontera “no-tan-libre” en dinámica de fluidos: las diferencias

Posted on by
Reply

En esta entrada tratamos de presentar de manera sencilla la siguiente pregunta

¿Cómo de importante es el lecho marino para las olas en la superficie?

Así tenemos que estudiar el problema de la evolución de la interfase entre dos fluidos cuando dichos fluidos se encuentran en un medio poroso acotado y, tras hacer unas simulaciones para ver por dónde iban los tiros, dimos los primeros pasos en el estudio matemático del problema. Sin embargo, pese a que en las simulaciones observamos grandes diferencias en los primeros resultados matemáticamente rigurosos no capturamos esos fenómenos.

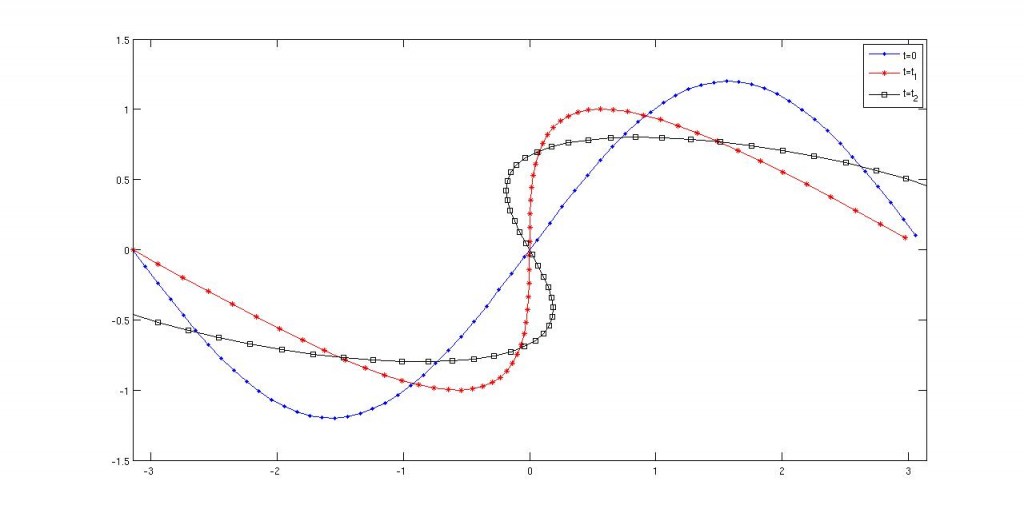
La primera pregunta que nos hacemos es ¿cuál es la evolución de la amplitud máxima de la ola? Para ellos lo que hacemos es estudiar

Lo que conseguimos probar es

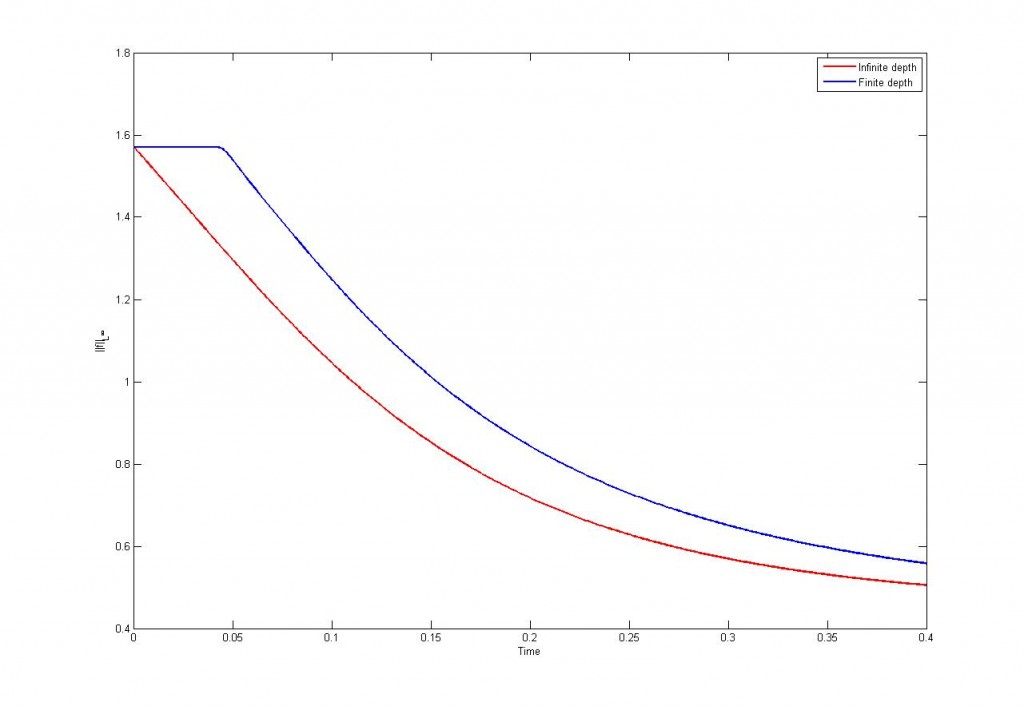
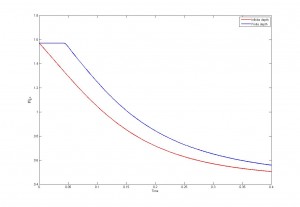
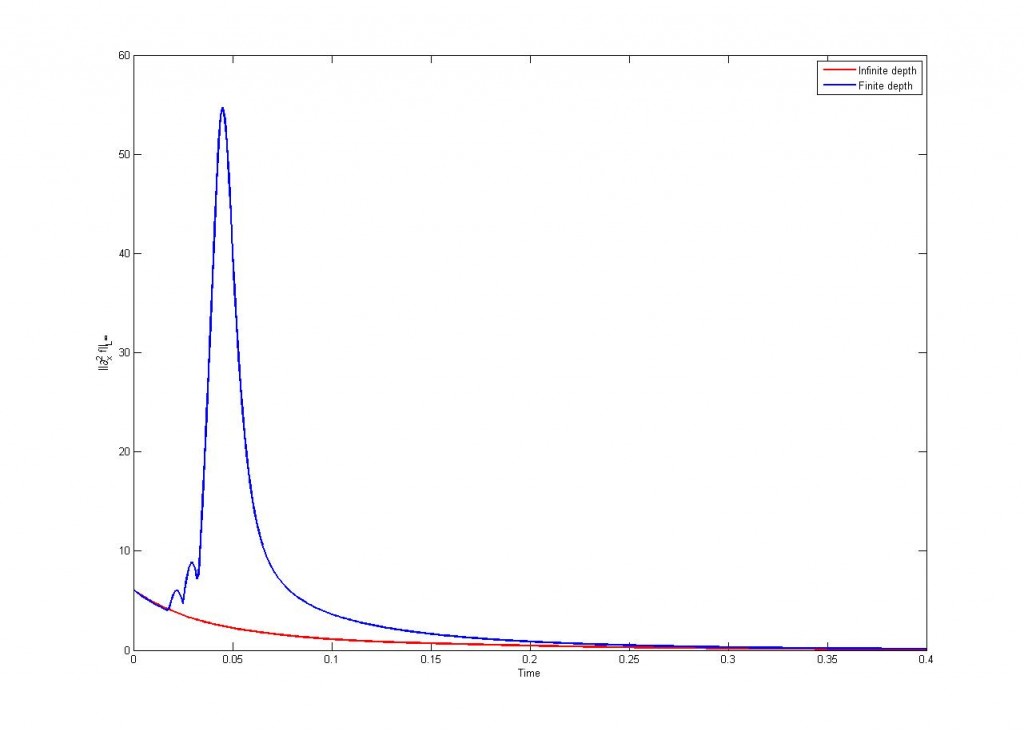
o, lo que es lo mismo, que la amplitud no puede crecer con el tiempo. Este resultado es idéntico al caso donde la profundidad es infinita. Sin embargo en las simulaciones habíamos visto que las diferencias a este nivel eran grandes:

Lo que ocurre es que la velocidad a la que cae la amplitud es distinta. En el caso de profundidad infinita tenemos

donde f_0(x)=f(x,0) es la ola inicial. En el caso de un medio acotado la amplitud evoluciona según

Así hemos obtenido la primera diferencia importante: la interfase en el caso de profundidad finita decae más despacio. 

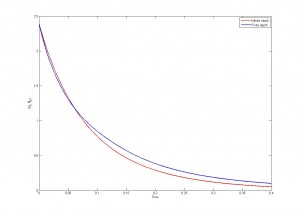
Ahora cabe preguntarse ¿cómo evoluciona \max_x|\partial_x f(x,t)|? Esta cantidad nos da una idea de cómo es la longitud de onda. Sabemos que en el caso donde el medio no está acotado se tiene que

si \max_x|\partial_x f(x,0)|<1 entonces \max_x|\partial_x f(x,t)|<\max_x|\partial_x f(x,0)|\;\; \forall t>0.

En el caso de que el medio tenga profundidad finita tenemos una condición (razonablemente complicada y que escribiremos F) que involucra no sólo a \max_x|\partial_x f(x,0)| si no también a \max_x|f(x,0)|:

si F(\max_x|\partial_x f(x,0)|,\max_x|f(x,0)|)\leq 0 entonces \max_x|\partial_x f(x,t)|\leq\max_x|\partial_x f(x,0)|\;\; \forall t>0.

Una consecuencia de esto es que si esa condición se satisface y entonces tenemos una cota superior para \max_x|\partial_x f(x,t)| y por lo tanto la ola no puede romper.

Bueno, ahora que sabemos cuándo la interfase no rompe cabe preguntarse si hay alguna situación en la que la interfase rompa. Y efectivamente obtenemos que hay datos tales que pasa lo siguiente:

Es más, podemos probar mediante una prueba asistida con ordenador, que existen datos iniciales tales que sólo rompen cuando la profundidad es finita. Es decir, que el fondo ayuda a que las olas rompan. Y si bien hemos probado estos teoremas en el caso de fluidos moviéndose en un medio poroso estos dos últimos resultados se pueden probar gratis para el caso de las water waves, i.e. la interfase entre un fluido incompresible e irrotacional siguiendo las ecuaciones de Euler y el aire.

–Referencias:

D. Córdoba, RGB, R.Orive, The confined Muskat problem: differences with the deep water regime.

–Nota: Con esta entrada participamos en el Carnaval de Matemáticas en su edición 26, organizado esta vez por ZTFNews.

–Nota 2: Con esta entrada participamos también en el Carnaval de Física en su edición XXXIV que organiza Hablando de Ciencia.

Problemas de frontera “no-tan-libre” en dinámica de fluidos: primeros pasos

Posted on by
2

Decía el señor Swett Marden que

“Un guijarro en el lecho de un pobre arroyuelo puede mudar el curso de un río”.

Parece una exageración y sin duda lo es, pero sirve para que nos hagamos la siguiente pregunta:

¿Cómo de importante es el lecho marino para las olas en la superficie?

Ésta es la pregunta que tratamos de contestar en este artículo. El problema que queremos entender es, dados dos fluidos incompresibles en un medio poroso acotado, ¿cómo se comporta la interfase entre ambos y que diferencias presenta con el caso en el que el medio no esta acotado? Bueno, vamos a trasladar ese problema físico a ecuaciones en derivadas parciales. Tenemos una densidad que presenta dos valores según estemos por encima o por debajo de la interfase, que denotamos por ,

Que los fluidos sean incompresibles y se muevan en un medio poroso acotado quiere decir que el dominio espacial de los fluidos es 

y que la velocidad satisface la Ley de Darcy y la condición de incompresibilidad

Estas ecuaciones se puede trasladar a una única ecuación para la interfase:

Ahora que tenemos el problema cabe preguntarnos si el hecho de que el dominio sea S y no \mathbb{R}^2 cambia mucho la situación. Para hacernos una idea podemos hacer unas simulaciones numéricas preliminares. Para ello consideramos un dato inicial y lo hacemos evolucionar en el caso donde el medio tiene profundidad finita (caso acotado) y también en el caso en el que el medio tiene una profundidad infinita (caso no acotado). Por supuesto el resto de los parámetros físicos son los mismos en ambas evoluciones. Así observamos lo siguiente

(Si no ves bien las imágenes pincha en ellas para hacerlas más grandes)

Parece claro a la vista de estos resultados que el hecho de que el medio esté acotado o no es relevante para las olas.

Una vez que tenemos el problema propuesto tenemos que empezar a sacar teoremas :-P. Evitando tecnicismos lo primero que probamos es

1) (Existencia y unicidad) que si el fluido de arriba es más ligero que el que está abajo el problema tiene una solución.

1.b) (Existencia y unicidad 2) que si el fluido de arriba es más pesado que el de abajo pero la interfase inicial es analítica existe una solución.

2) (Efecto regularizante) que dicha solución se vuelve muy regular (analítica) para cualquier t>0 (compárese con la ecuación del calor aquí.)

De momento estos 3 teoremas son idénticos en su enunciado a los teoremas cuando la profundidad es infinita. ¿Sorprendido? Bueno, esto sólo quiere decir que para probar matemáticamente las diferencias que hemos visto en los vídeos y las imágenes anteriores tenemos que trabajar un poco más, así que sed pacientes y esperad a la siguiente entrada ;-).

Bueno, si os veis muy impacientes podéis leer (o, en su caso, releer) ésta, ésta y esta entrada.

–Referencias:

D. Córdoba, RGB, R.Orive, The confined Muskat problem: differences with the deep water regime.

–Nota: Con esta entrada participamos en el Carnaval de Matemáticas en su edición 26, organizado esta vez por ZTFNews.

–Nota 2: Con esta entrada participamos también en el Carnaval de Física en su edición XXXIV que organiza Hablando de Ciencia.

Las matemáticas como ciencia experimental

Posted on by
4
Actualmente cuando uno piensa en problemas sin resolver en física piensa en la Teoría del Todo, en el bosón de Higgs o en los límites de validez de la mecánica cuántica. Sin embargo, existen problemas que son fáciles de entender que aún no tienen respuesta. Problemas que sólo involucran a la mecánica de Newton y que todavía no sabemos cómo atacar. Vamos a introducir el que nos ocupa con un experimento que puede ser fácilmente realizado en casa. Continue reading →

Resolviendo la ecuación de ondas…

Posted on by
Reply
Tradicionalmente los matemáticos que trabajamos en el área de ecuaciones en derivadas parciales estudiamos problemas que vienen de procesos físicos. Es el caso de la ecuación del calor, la ecuación de Poisson o la ecuación de ondas. En esta entrada vamos a exponer dos métodos para resolver la ecuación de ondas. Estos métodos al tener un planteamiento distinto dan una información distinta. Veremos así diferencias entre pensar en las ecuaciones sólo o pensar en el fenómeno que modelizan. La ecuacion de ondas es
\displaystyle\partial_t\partial_t u=\partial_x\partial_x u,
junto a dos valores iniciales (tiene dos derivadas en tiempo) y las condiciones de contorno, que aquí tomamos dirichlet homogéneas. Esta ecuación refleja la separación del equilibrio de la cuerda en tiempo t y en el punto x.
Jean Le Rond D’Alembert demostró que si consideramos toda la recta (es decir, sin contornos) entonces podemos escribir la solución como una superposición de ondas, una que viaja hacia la derecha y otra que viaja hacia la izquierda. Estas ondas se escriben en función de los valores iniciales. Podemos hacer lo mismo en dominios acotados o semi acotados, pero es más lío.
Esta aproximación es puramente teórica, muchas ecuaciones admiten solución en forma de onda viajera (por ejemplo la de Fisher-Kolmogorov, \partial_t u=\partial_x\partial_x u +u(1-u) ). En este caso podemos esperarlo si observamos que podemos ‘factorizar’ el operador como dos operadores de transporte   Continue reading →

De cuerdas y tambores, o cómo la física aparece en un problema de matemáticas

Posted on by
Reply
Cualquier estudiante de física tiene claro o al menos intuye cómo aparecen las matemáticas al estudiar problemas de física. Hoy vamos a hablar de cómo aparece la física en un teorema abstracto de matemáticas. Continue reading →

Proteinas, ¡dobláos!

Posted on by
Reply

El “misterio” del plegamiento de proteinas está más cerca de su resolución: científicos en China han descubierto la ley que relaciona el comportamiento del plegado con la temperatura [1].

Hasta ahora se había pensado que las proteínas, largas cadenas de aminoácidos, se plegaban de modo “mecánico” (clásico), de modo que la proteína tenía que pasar por todos los estados intermedios hasta la forma funcional final. Simulaciones se habían llevado a cabo utilizando modelos clásicos de plegamiento de proteinas.

Imagen del plegamiento de una proteina. (Wikipedia)

Las proteinas se pliegan hasta su forma funcional, que es la de mínima energía

No obstante, los posibles disposiciones en que las proteínas se pueden doblar son MUCHAS [imaginémonos de cuantas maneras se puede doblar una cuerda muy larga], y la forma funcional es una determinada de estas disposiciones. En concreto, esta forma funcional sería el mínimo de energía en el plegado de la proteína, y parece ser que este mínimo no depende del modo en que se llega a la forma funcional (clásico o cuántico).

Además, los biólogos tienen datos que avalan que este proceso es muy sensible a la temperatura, y lo extraño es que no sigue la ley de Arrhenius [1](tendría que ser lineal en el logaritmo de la tasa de plegado con la inversa de la temperatura), sino que se comporta de modo no-lineal.

Lo que proponen estos científicos es que las proteínas no se mueven de modo mecánico hasta su forma final, sino que realizan un “salto cuántico” hasta ella. De este modo, al no tener que evaluar todas esas disposiciones, este plegamiento puede ser muy rápido (del orden de nanosegundos).

Utilizando este método, los científicos son capaces de predecir la dependencia de la tasa de plegado con la temperatura y sus resultados se ajustan bastante bien con los datos experimentales [2].

Referencias:

[1] Enlace en inglés, desde el MIT technology review blog: http://www.technologyreview.com/blog/arxiv/26421/?ref=rss

[2] “Ecuación de Arrhenius” en la wikipedia. Nivel básico en español o más completo en inglés.

[3]  L. Luo and J. Lu, “Temperature Dependence of Protein Folding Deduced from Quantum Transition”, eprint arXiv:1102.3748 [arxiv]

El oscilador armónico – Parte I

Posted on by
3

Hola a todos.
Esta entrada es mi primera contribución al blog, y siendo físico me gustaría comenzar con el que es el ladrillo de la física: el oscilador armónico.
El nombre, que nos da una idea de a qué nos estamos enfrentando, indica el movimiento de algo que se repite en el espacio y en el tiempo. Matemáticamente, siendo más estrictos, un movimiento armónico sería el descrito por una función “seno” o “coseno” . La palabra “armónico”, procedente del griego, nos da la idea de una conveniente proporcion y correspondencia entre unas y otras cosas. El concepto aparece en música, como la unión de sonidos acordes, y Kepler (amante de la música y con su mente puesta en ella) lo utilizaba como expresión de belleza y unión entre las matemáticas y el movimiento celeste. [Vease “La armonía de los mundos“] Continue reading →