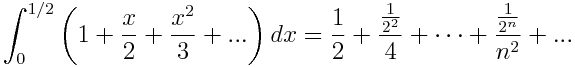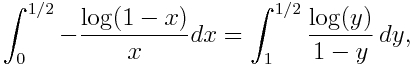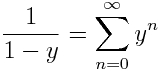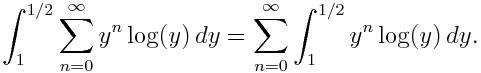En esta nueva entrada de la serie de las paradojas (las primeras estradas son http://scientiapotentiaest.ambages.es/?p=244 y http://scientiapotentiaest.ambages.es/?p=266) nos vamos a centrar en las paradojas que vienen de la probabilidad. Y es que la probabilidad pese a ser algo bastante mencionado en la vida diaria no es entendida por mucha gente.

Voy a comenzar tratando el problema de Monty Hall. Este problema es muy divertido, porque todo el mundo al que se lo contemos dirá que es muy intuitivo. ¡El problema es que para cada uno será intuitiva una respuesta distinta!

Supongamos que estamos en un programa de estos de la tele. En este programa hay tres puertas. Una de las tres tiene un premio y las otras dos no tienen nada. La puerta que tiene el premio se elige al azar de manera equiprobable. El juego consiste en elegir una puerta. Tras nuestra elección, el presentador, que sabe dónde está el premio, abre una de las dos puertas que no hemos elegido y que no tiene nada. Tras esto nos pregunta si queremos cambiar de puerta. La pregunta viene ahora, ¿qué nos sale mejor como jugadores? ¿cambiar nuestra primera elección o dejarla estar?

Observamos que el premio no cambia de puerta mientras nosotros jugamos.

La respuesta correcta es que siempre nos sale mejor cambiar de puerta. Sí, amigos lectores, es mejor cambiar. ¿Qué no me creéis? Vamos a ver si os convenzo. Como el premio está en una de las puertas de manera equiprobable la probabilidad de que el premio se encuentre en la puerta que hemos elegido al comenzar a jugar es 1/3. Ahora el presentador abre una de las otras dos puertas sin descubrir el premio. ¿Cuál es la probabilidad de que nuestra puerta esconda el premio? LA MISMA, 1/3. Por lo tanto si cambiamos de puerta nuestra nueva elección tendrá probabilidad 2/3. Vamos a ilustrar esto un poco más mirando los posibles casos. Vamos a suponer que elegimos siempre la puerta 1, como todo es simétrico todos los casos estarán reflejados igualmente.

1) El coche está en la puerta 1.
1.a) Cambiamos de puerta y perdemos.
1.b) No cambiamos y ganamos.
2) El coche está en la puerta 2.
2.a) Cambiamos de puerta y ganamos.
2.b) No cambiamos y perdemos.
3) El coche está en la puerta 3.
3.a) Cambiamos de puerta y ganamos.
3.b) No cambiamos y perdemos.

Hagamos el recuento: Si cambiamos ganamos 2 veces frente a una que perdemos. Si no cambiamos la situación es recíproca. Como hay 3 casos posibles la probabilidad de ganar cambiando es 2/3.

Otra manera de convencerse es aumentar el número de puertas. Supongamos que tenemos 100 puertas. Entonces la probabilidad de que el premio esté en nuestra puerta es 1/100. Tras elegir, el presentador abre todas las puertas menos dos, la que tu elegiste y otra, de manera que ninguna de las abiertas mostrase el premio. Ahora parece claro que lo mejor es cambiar.

Otra paradoja que invariablemente se estudia en los cursos iniciales de probabilidad es la paradoja de los hijos (a falta de un nombre mejor en castellano). Supongamos que la probabilidad de que nazca un chico o una chica es la misma, 50%, y que el sexo de cada hijo es independiente del sexo de los demás hermanos. Vamos con el problema. La señora López tiene dos vástagos. Supongamos, a modo de calentamiento, que el hijo mayor de la señora López es un niño, ¿cuál es la probabilidad de que el menor sea niña? La respuesta, claro, es 50%. Ahora se nos plantea un problema ligeramente distinto: Supongamos que uno de los hijos de la señora López es niño, ¿cuál es la probabilidad de que el otro hijo también sea niño? ¿50%? Veamos los casos tal cuál está escrito (observando que la familia está fija para los más puntillosos) y ordenando los niños por edad:

1) Chico-chico
2) Chica-chico
3) Chico-chica

Hay 3 casos posibles y sólo 1 es el que nos preguntan. Como son equiprobables la probabilidad de que ambos hijos de la señora López sean niños es 1/3. El truco aquí está en que al decir que uno de los hijos es chico perdemos información sobre su edad. En la primera pregunta tenemos más información y podemos descartar más casos.

La probabilidad se va descubriendo un poco farragosa y “extraña” en ocasiones. Sin embargo todavía no hemos tratado la principal fuente de problemas al tratar con la probabilidad. Me refiero a la ambigüedad. Las palabras “al azar” no tienen un significado preciso y se usan con más asiduidad de la recomendable. Esto quedó claramente expuesto en la obra de J. Bertrand “Calcul des probabilités”. En este manual propuso un enunciado y dio varias respuestas al problema, todas bien lógicas y correctas. El problema era que en cada uno la definición de “al azar” era distinta. Es ahora cuando nos ponemos técnicos. En la entrada anterior ya mencionamos cosas como “medidas” de conjuntos (ver la entrada anterior). Eso nos volverá a ser útil, pues la manera matemática de dar sentido a las palabras “al azar” utiliza esas ideas. En matemáticas un “espacio de probabilidad” es un espacio de sucesos posibles en nuestro experimento, una manera de agruparlos en conjuntos y una manera de “medir la probabilidad” cada uno de estos conjuntos de sucesos. Claro está que la definición precisa es mucho más técnica. Así la idea que quiero dejaros es que esas tres cosas abstractas es lo que da sentido a la palabra “azar”.

El ejemplo que más me gusta de esto es la paradoja de Bertrand. Consideremos un círculo con un triángulo equilatero inscrito. La pregunta ahora es ¿cuál es la probabilidad de que una cuerda trazada “al azar” sea más larga que los lados del triángulo? Veamos las tres maneras clásicas de calcular dicha probabilidad:

1) Supongamos, sin pérdida de generalidad, que uno de los extremos de la cuerda coincide con uno de los vértices del triángulo. En ese caso al quedar la circunferencia dividida en 3 trozos iguales y coincidir uno con el conjunto donde la cuerda es más larga que el lado del triángulo concluimos que la probabilidad pedida es 1/3. Aquí el espacio de sucesos es el conjunto de puntos de la circunferencia y la medida de probabilidad asociada es la longitud del arco considerado dividido la longitud total de la circunferencia.

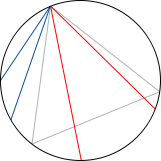
2) Consideremos ahora un radio perpendicular a uno de los lados del triángulo. Esto de nuevo nos facilita la vida pero no perdemos generalidad. Ahora trazamos la cuerda de manera perpendicular a dicho radio por un punto aleatorio del mismo. La probabilidad de que la cuerda sea mas larga que el lado es justamente 1/2 si la trazamos con estas reglas. Aquí el espacio de sucesos es el conjunto de puntos del radio y la medida de probabilidad es la longitud del segmento considerado dividido por la longitud total.

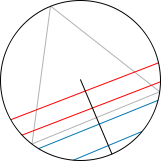
3) Ahora nuestro experimento consiste en elegir el punto medio de la cuerda. Si trazamos la cuerda con esta regla la probabilidad de que la longitud de la cuerda sea mayor que la del lado del triángulo es la misma que la probabilidad de que el punto medio de la cuerda esté en un círculo concentrico inscrito en el triángulo de radio la mitad (y área 1/4 del área del círculo original). Por lo tanto la probabilidad será 1/4. Aquí el espacio de sucesos es el conjunto de puntos del círculo y la medida de probabilidad es el área del conjunto de puntos considerado dividido entre el área del círculo original.

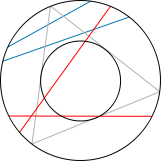
La paradoja aquí estriba en que para una pregunta tenemos tres respuestas. Además, eligiendo la definición de “azar” todas son correctas.

Creo que ha quedado claro que cuando decimos cosas como “aleatorio” o “al azar” no estamos en realidad diciendo nada y que debemos entrar, aunque no queramos, en tecnicismos para evitar este tipo de paradojas.

— Nota: Las imágenes han sido obtenidas de la Wikipedia en inglés

— Nota: Con esta entrada participamos en el Carnaval de Matemáticas en su edición 2.6 (albergado por “La vaca esférica” , http://lavacaesferica.com/).