Me comentó David que sería interesante que explicase un poquito de lo que significa la reversibilidad temporal desde el punto de vista de las ecuaciones en derivadas parciales (EDPs de ahora en adelante). Es decir, sin mencionar nada de entropías. Este es un tema muy interesante e importante aunque a primera vista parezca una tontería. Lo hemos puesto como una serie de dos entradas. La primera (esta que estás leyendo) presentará las EDPs más fáciles y estudiará sus propiedades de cara a la reversibilidad temporal. En la segunda veremos la derivación de unos modelos más complicados y trataremos de entender dónde aparece la irreversibilidad temporal. Lo cierto es que en cierto modo es llamativo, pues las leyes de Newton son reversibles en tiempo y muchas (casi todas) de las ecuaciones de las que hablaremos surgen de ellas.
Viendo qué ocurre:
Para entender qué quiere decir y qué implica la reversibilidad (o irreversibilidad) temporal hemos de comprender primero los ejemplos más básicos de EDPs. Como dato para los técnicos supondré que todos los problemas están puestos para ![(t,x)\in [0,T]\times\mathbb{R} (t,x)\in [0,T]\times\mathbb{R}](https://s0.wp.com/latex.php?latex=%28t%2Cx%29%5Cin+%5B0%2CT%5D%5Ctimes%5Cmathbb%7BR%7D&bg=T&fg=000000&s=0) . Inmerso en el texto hay imágenes .jpg, imágenes animadas .gif (pinchad en ellas para que empiecen a moverse) y código Matlab (¡usadlo si podéis!).
. Inmerso en el texto hay imágenes .jpg, imágenes animadas .gif (pinchad en ellas para que empiecen a moverse) y código Matlab (¡usadlo si podéis!).
La ecuación del transporte:
Comenzaremos con la ecuación del transporte unidimensional con coeficientes constantes. Esta es la EDP más sencilla que podemos poner.

Supondremos que 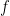 es una función derivable con derivada continua una vez. La solución de esta ecuación es
es una función derivable con derivada continua una vez. La solución de esta ecuación es 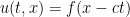 (¡comprobadlo!). Esta ecuación se llama ‘del transporte’ porque lo que hace es eso ‘mueve’ nuestra distribución inicial
(¡comprobadlo!). Esta ecuación se llama ‘del transporte’ porque lo que hace es eso ‘mueve’ nuestra distribución inicial  . Si queremos cambiar el sentido del tiempo hemos de hacer el cambio
. Si queremos cambiar el sentido del tiempo hemos de hacer el cambio  por
por  . Entonces la nueva ecuación es
. Entonces la nueva ecuación es
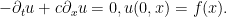
Observamos que el cambiar el tiempo de sentido es equivalente a cambiar el signo de  . Si utilizamos el código que propongo con varios valores de
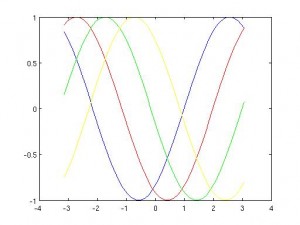
. Si utilizamos el código que propongo con varios valores de  observamos que este parámetro es una velocidad. Por lo tanto, parece natural que cambiar el sentido del tiempo cambie el sentido del movimiento. Es decir, que si para
observamos que este parámetro es una velocidad. Por lo tanto, parece natural que cambiar el sentido del tiempo cambie el sentido del movimiento. Es decir, que si para 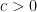 íbamos a la derecha, para tiempos negativos (o equivalentemente
íbamos a la derecha, para tiempos negativos (o equivalentemente 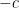 ) tenemos que ir a la izquierda. Concluímos así que la ecuación del transporte es reversible en tiempo y que la reversibilidad es muy natural si partimos del proceso físico que se modela con esta ecuación.
) tenemos que ir a la izquierda. Concluímos así que la ecuación del transporte es reversible en tiempo y que la reversibilidad es muy natural si partimos del proceso físico que se modela con esta ecuación.
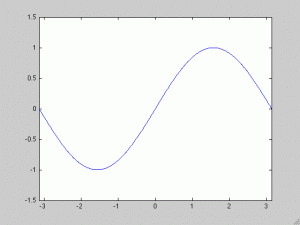
Otra consecuencia, ésta mucho más sutil, de la reversibilidad temporal es que nuestra solución NUNCA va a ser mejor que nuestro dato inicial 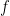 . Esto es obvio en este caso porque tenemos una solución explícita, pero es cierto en general. Si
. Esto es obvio en este caso porque tenemos una solución explícita, pero es cierto en general. Si  tuviese más derivadas que
tuviese más derivadas que 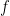 entonces dando la vuelta al tiempo tendríamos una contradicción.
entonces dando la vuelta al tiempo tendríamos una contradicción.
function [u,x,t]=transporte(dx,dt,f,c)
%%
%Funcion que me aproxima la solucion exacta (conocida) de la
%ecuacion del transporte u_t+cu_x=0 con dato inicial
% u(0,x)=f(x), paso espacial dx y paso temporal dt.
%f sera una funcion
% Rafael Granero Belinchon
%%
%Definicion de parametros:
T=10; %El tiempo final
t=0:dt:T; %el vector de tiempos
x=-pi:dx:pi; %el vector de espacio donde queremos
%nuestra aproximacion. No necesitamos condiciones de borde ¿por que?
u=zeros(length(x),length(t));
F=feval(f,x);
%Calculo de la solucion:
%La solucion del problema anterior es u(x,t)=f(x-ct)
u(:,1)=F;
for j=2:length(t)
u(:,j)=feval(f,x-c*t(j));
plot(x,u(:,j-1));%Representacion de los resultados
drawnow
end
function f=prueba(x)
f=sin(x);
La ecuación de ondas:
La siguiente ecuación es el paradigma de ecuación hiperbólica. Me refiero a la ecuación de ondas. Viendo el nombre está claro qué proceso físico quiere describir ¿no?.
Esta ecuación se escribe
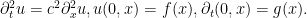
Visualmente parece mucho más complicada que la ecuación del transporte… sin embargo en realidad es igual (al menos en un cierto sentido). Vamos a escribirla como un sistema. Para ello definimos el sistema
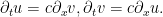
Si ahora derivamos en tiempo la ecuación para 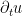 y utilizamos la segunda ecuación obtenemos
y utilizamos la segunda ecuación obtenemos

Es decir, que la ecuación de ondas no es más que dos transportes acoplados. Sin embargo todavía podemos hacerlo mejor. Podemos darnos cuenta de que el operador diferencial se puede escribir como

y por lo tanto si tenemos 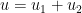 con
con

tenemos una solución de la ecuación original. Concluímos que, como la ecuación del transporte era reversible, la ecuación de ondas, que se puede escribir como un par de ecuaciones del transporte debe ser reversible también.
La ecuación del calor:
Esta ecuación es parabólica. Se escribe
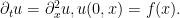
Visualmente parece estar a medio camino entre la ecuación del transporte y la ecuación de ondas, sin embargo su comportamiento en radicalmente distinto. Para convencernos de ello podemos ‘jugar’ un poco con el código Matlab que adjunto. Los datos iniciales por defecto son los mismos, pero os animo a cambiarlos.
function [u,x,t,mx]=heatff(N,dt,K)
%%
%Funcion que me aproxima la solucion de la
%ecuacion del calor con dato inicial seno
%con condiciones periodicas (para usar FFT)
%N es el numero de nodos espaciales que se quieren
%usar. dt es el paso temporal que se quiere.
%K es la constante de difusion.
%Devuelve el espacio, el tiempo, la aproximacion de
%la solucion y el maximo de dicha solucion en cada tiempo
%Rafael Granero Belinchon
%%
T=5;%Tiempo final
dx=2*pi/(N-1);
x=-pi:dx:pi;%Espacio
t=0:dt:T;%Tiempo
uo=sin(x);%dato inicial
for k=1:N/2 %Operador laplaciano en espacio de fourier
L(k)=(k-1)*(k-1);
L(k+N/2)=(N/2-k+1)*(N/2-k+1);
end
L=K*L;
u(:,1)=uo’;
mx(1)=max(uo);
for l=1:length(t)
u(:,l+1)=ifft(exp(-L*dt*l).*fft(uo))’;%solucion
mx(l+1)=max(u(:,l+1));%Evolucion del maximo
plot(x,u(:,l));axis([-pi,pi,-1,1]);%Representacion de los resultados
drawnow
end
end
Para estudiar esta ecuación vamos a utilizar la transformada de Fourier. Para la transformada de Fourier de 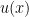 usaremos la notación
usaremos la notación 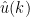 . Así si transformamos la ecuación en espacio obtenemos las ecuaciones diferenciales ordinarias (EDOs a partir de ahora) indexadas en la longitud de onda
. Así si transformamos la ecuación en espacio obtenemos las ecuaciones diferenciales ordinarias (EDOs a partir de ahora) indexadas en la longitud de onda 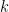 siguientes
siguientes
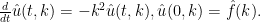
Esta ecuación la podemos resolver explícitamente
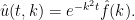
Observemos ahora qué quiere decir el cambio del sentido del tiempo. De nuevo hagamos el cambio 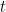 por
por  . La ecuación nos queda
. La ecuación nos queda

No se ve nada claro, sin embargo, si buscamos los efectos del cambio en la solución explícita tenemos
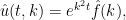
de manera que cuando invirtamos la transformada de Fourier estamos calculando una convolución con una función que no está acotada, ni tiene ninguna potencia integrable… Vamos, que nuestra solución (que existe explícitamente) no está en ningún espacio razonable ni con propiedades físicas razonables. Por ejemplo, si  es la temperatura, entonces su integral (que es el calor) debe ser finita. Pues si damos la vuelta al tiempo obtenemos calor infinito para cualquier tiempo. Concluímos que la ecuación del calor NO es reversible en tiempo.
es la temperatura, entonces su integral (que es el calor) debe ser finita. Pues si damos la vuelta al tiempo obtenemos calor infinito para cualquier tiempo. Concluímos que la ecuación del calor NO es reversible en tiempo.
Una propiedad que a veces se da en las ecuaciones irreversibles y que es bien interesante es el ‘efecto regularizante’. Es decir, tu dato inicial 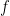 es continuo (por ejemplo), pero tu solución
es continuo (por ejemplo), pero tu solución  es infinitamente derivable para todo tiempo (positivo). Como ya hemos mencionado antes, este comportamiento difiere del de las ecuaciones hiperbólicas usuales. La prueba de esto se puede hacer sin más que multiplicar por
es infinitamente derivable para todo tiempo (positivo). Como ya hemos mencionado antes, este comportamiento difiere del de las ecuaciones hiperbólicas usuales. La prueba de esto se puede hacer sin más que multiplicar por  e integrar por partes en espacio (¡comprobadlo!). Después basta observar que la ecuación es invariante por derivación tanto en tiempo como en espacio (¡Concluid el argumento!).
e integrar por partes en espacio (¡comprobadlo!). Después basta observar que la ecuación es invariante por derivación tanto en tiempo como en espacio (¡Concluid el argumento!).
Vistos estos 3 ejemplos parece que hay una relación entre la ‘simetría’ del problema y su reversibilidad temporal. Quiero decir que, al menos de momento, las ecuaciones que tienen el mismo número de derivadas temporales que espaciales han resultado ser reversibles, mientras que las que no las tienen son irreversibles.
Otra cosa que se nos puede ocurrir es que las ecuaciones reversibles sean las que ‘no tiendan a nada’. Así vemos que la ecuación del calor tiende a ser idénticamente cero (necesita tiempo infinto para llegar a serlo) mientras que la ecuación del transporte sólo se movía por el espacio.
Veamos otro ejemplo:
La ecuación de Schrödinger:
Esta ecuación, clave en mecánica cuántica, se escribe
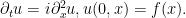
Si repetimos el análisis que hicimos para la ecuación del calor obtenemos que la solución es
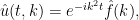
que tiene un comportamiento oscilatorio. Por lo tanto, pese a tener una derivada en tiempo y dos en espacio se parece más a una ecuación de ondas que a una ecuación del calor. Observamos que el hecho de que aparezca la unidad imaginaria hace que  no sea real, sino compleja. Por lo tanto tiene una función conjugada. Si ahora cambiamos el sentido del tiempo observamos que para la función conjugada
no sea real, sino compleja. Por lo tanto tiene una función conjugada. Si ahora cambiamos el sentido del tiempo observamos que para la función conjugada  la ecuación es la misma. Por lo tanto si
la ecuación es la misma. Por lo tanto si  es nuestra solución con el tiempo hacia delante,
es nuestra solución con el tiempo hacia delante,  es una solución con el tiempo hacia atrás. Por lo tanto la ecuación de Schrödinger es reversible. Este ejemplo desmonta la hipótesis de que als reversibles debían tener el mismo número de derivadas en espacio y en tiempo.
es una solución con el tiempo hacia atrás. Por lo tanto la ecuación de Schrödinger es reversible. Este ejemplo desmonta la hipótesis de que als reversibles debían tener el mismo número de derivadas en espacio y en tiempo.
function [u,x,t,L2,mx]=schrodinger(N,dt)
%%
%Funcion que me aproxima la solucion de la
%ecuacion de schrodinger con dato inicial seno
%con condiciones periodicas (para usar FFT)
%N es el numero de nodos espaciales que se quieren
%usar. dt es el paso temporal que se quiere.
%Devuelve el espacio, el tiempo, la aproximacion de
%la solucion, la norma L^2 de dicha solucion en cada tiempo
%y el maximo de la solucion en todo tiempo.
%Rafael Granero Belinchon
%%
T=5;%Tiempo final
dx=2*pi/(N-1);
x=-pi:dx:pi;%Espacio
t=0:dt:T;%Tiempo
uo=sin(x);%dato inicial
for k=1:N/2 %Operador laplaciano en espacio de fourier
L(k)=(k-1)*(k-1);
L(k+N/2)=(N/2-k+1)*(N/2-k+1);
end
L=i*L;
u(:,1)=uo’;
L2(1)=norm(uo)*dx;
mx(1)=max(abs (uo));
for l=1:length(t)
u(:,l+1)=ifft(exp(-L*dt*l).*fft(uo))’;%solucion
L2(l+1)=norm(u(:,l+1))*dx;%Evolucion de la norma L^2
mx(l+1)=max(abs(u(:,l+1)));%Evolución del máximo
plot(x,real(u(:,l)));axis([-pi,pi,-1,1]);%Representacion de los resultados
drawnow
end
end
Como dato anécdotico de esta ecuación hacemos notar que no puede reflejar efectos relativistas (¿por qué?).
En la próxima entrada, enlazando con esta, trataré la derivación desde la mecánica hamiltoniana de los modelos que se utilizan en mecánica de fluidos y trataré de explicar dónde aparece la irreversibilidad en el proceso. Sin embargo, esto es algo que no está ‘completamente entendido’ todavía.
que tiene, al menos, dos derivadas en
, y supongamos además que dicha solución se va muy rápido a cero cuando
se hace muy grande. Dicha solución tendrá un mínimo (o ínfimo), y un máximo (o supremo) y sus posiciones dependerán del tiempo. Como la función tiende a cero en el infinito estos valores se alcanzan (es decir, no son ínfimos/supremos). Denotemos el punto donde
alcanza su mínimo como
y el punto donde
alcanza su máximo como
. Por lo tanto, fijo
,
obtenemos, si
es el punto de mínimo, la siguiente ecuación
,
.






