Hace bastante tiempo escribí la primera parte de esta serie, pero dado que estoy muy ocupado soy un poco vago, he tardado bastante en ponerme a escribir la segunda parte.
Hoy, y apoyándome en el cálculo variacional (tanto en el concepto físico como en el desarrollo matemático), revisaremos el oscilador armónico pero esta vez lo haremos desde el punto de vista Lagrangiano.
Ante todo, ¿por qué debería interesarnos?
Es muy raro el problema que nada más que se puede resolver de una manera. En concreto, el problema de cómo enfrentarnos a problemas sobre el movimiento es uno que ha recibido bastante atención a lo largo de los últimos siglos y una diversidad de enfoques.
En tiempos de Newton, el mayor problema radicaba en describir el movimiento como una entidad matemática. Para ello, y junto a Leibniz (aunque de manera totalmente independiente), fundaron el calculo infinitesimal. Esto les permitía describir de manera rigurosa lo que ocurre cuando cambias algo “muy poco”. Por ejemplo, la velocidad se puede describir como la variación en la posición de un cuerpo cuando varías el tiempo “muy poco” (una variación infinitesimal en el tiempo). Este concepto tan poderoso es la derivada.
Además, utilizando el sistema de coordenadas cartesianas, podían describir de manera analítica las posiciones en 2 o 3 dimensiones sin ningún problema.
Una vez que ya se había desarrollado el cálculo infinitesimal, y que se podían escribir (y resolver) leyes del movimiento como ecuaciones diferenciales (c 41 omo las que vimos en la primera entrada de esta serie), los científicos de la época, en su afán de comprender la naturaleza, trataron de derivar todas esas leyes del movimiento a partir de un reducido corpus de principios esenciales. Uno de esos principios es el principio de mínima acción, del que ya hemos hablado aquí.
Euler y Lagrange dieron con un método, que se llamaría “Mecánica Lagrangiana“, que permitía obtener (bajo ciertas suposiciones) los mismos resultados que las ecuaciones de Newton sin tener que particularizar los grados de libertad del sistema.
La Mecánica Lagrangiana se basa en el concepto de Lagrangiano (que ya nombramos en su día). Éste objeto es una función que depende de la energía cinética y potencial de las partículas que queremos describir, y se define como:
(1),
donde la energía cinética, , depende de la masa
y la velocidad total,
de cada particula
, y se suma sobre las contribuciones de cada una de ellas; y la energía potencial, $E_p$ es, en general, una función que depende de la posición y velocidad de las partículas, aunque sea muy usual, no obstante, que tratemos con “fuerzas conservativas“, que no dependen de la velocidad.
Los grados de libertad son el número total de cantidades cuya evolución en el tiempo necesitaremos conocer para describir el movimiento. Por ello, serán también el número de ecuaciones diferenciales que habremos de resolver.
El hecho de que las leyes no dependan del particular conjunto de coordenadas que se utilicen para describir el movimiento se llama “invariancia” bajo cambio de coordenadas, y es de suma importancia en este y los sucesivos desarrollos de la mecánica.
Pero esta entrada se refiere al oscilador armónico. ¿Cómo se aplican esos conceptos para este caso particular?
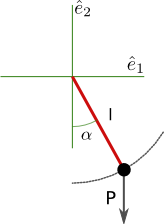
Diagrama de un péndulo bajo la acción de la gravedad, mostrando el sistema de coordenadas y el vector peso.
Partamos, de nuevo, desde el ejemplo del péndulo que se movía en el plano. En principio, nuestra partícula (la cabeza del péndulo) tendría 4 grados de libertad, esto es, necesitaría 4 números para describir su estado de movimiento:
- 2 números especificando su posición el el plano,
- 2 números para describir su velocidad,
.
No obstante, la cuerda que une el péndulo con el origen de coordenadas impone 2 ligaduras:
- El cuerpo ha de moverse en el extremo de la cuerda. Esto es, su distancia con respecto al centro del movimiento es siempre
:
- La velocidad ha de ser tangente al movimiento, pues de otra manera el cuerpo se saldría de su trayectoria circular:
En general, si tenemos particulas moviéndose en un espacio de
dimensiones sujetas a
ligaduras, el número de grados de libertad será
, donde el 2 da cuenta de que el número de grados de libertad incluye las velocidades.
Esto nos da 4-2=2 grados de libertad (gdl) para la descripción del movimiento del péndulo en 2 dimensiones.
Una vez que tenemos el número de gdl, ¿cómo utilizamos el concepto de invariancia a nuestro favor? La invariancia indica que, siempre que los grados de libertad que usemos sean independientes entre sí, estos servirán para describir el movimiento del péndulo. A estas cantidades las llamaremos coordenadas generalizadas.
Podríamos resolver el problema al estilo “vectorial”, como ya lo hicimos en la entrada anterior. No obstante, sería más provechoso explotar la simetría del problema y utilizar una sola coordenada que describa de manera unívoca la posición de la partícula, y su velocidad sea una expresión sencilla. Resulta que esa coordenada es el ángulo que forma el péndulo con la vertical, .
AVISO: quizás este paso que acabamos de hacer sea el más importante a la hora de resolver el problema al estilo Lagrangiano. Una correcta elección de nuestros grados de libertad puede simplificar el problema, mientras que una incorrecta puede hacerlo absurdamente complicado.
*Adoro* cuando el método se muestra en cursos universitarios y se suele acompañar de la frase “como es trivial observar, escogeremos esta coordenada”. Es relativamente fácil cuando has hecho chorrocientos problemas similares; es “altamente no trivial” cuando lo haces por primera vez.
No es fácil (repito: NO ES FÁCIL) escoger los grados de libertad adecuados, y es una habilidad que mejora con la práctica y un mayor conocimiento de las matemáticas tras la mecánica de Lagrange.
Ahora que tenemos los grados de libertad, y recordando que nuestra cantidad importante es el Lagrangiano, vamos a a ver cómo expresar las energía cinética y potencial en nuestra coordenada particular.
Habíamos visto en la entrada anterior que podíamos escribir las coordenadas x e y como , donde
es la longitud del péndulo y
es el ángulo que subtiende el péndulo con la vertical. La única variable en estas sustituciones es, pues,
.
La energía cinética para una partícula es fácil de obtener, pues solamente tenemos que derivar cada una de las componentes cartesianas de la posición con respecto a nuestra variable y sustituir
dónde, en esta última igualdad, hemos hecho uso de .
La energía potencial, por otra parte, es la debida al campo gravitatorio sobre la partícula. Para ello, tendríamos que obtener el potencial a partir de la fuerza que actúa sobre la partícula (y que ya conocemos). Podemos asumir que, en la superficie terrestre, el peso, o fuerza producida por el campo gravitatorio tiene la forma $P=-mg$ dirigida en la dirección vertical y en sentido hacia el suelo. Un campo conservativo es aquel que puede ser caracterizado como , donde
es el gradiente del potencial
.
El potencial del que esta derivada la fuerza es , puesto que si derivamos esto en dirección vertical, obtenemos el peso, cuya expresión está dada un poco más arriba. Si escribimos esto en nuestra coordenada particular,
, obtenemos:
De modo que, uniendo la energía potencial y la cinética, podemos obtener una expresión para el Lagrangiano (dado por la fórmula (1) ) en función de nuestros grados de libertad, y
:
Ecco! Este resultado nos permite, como ya dijimos en otra entrada, obtener a ecuación del movimiento del sistema… ¡utilizando el principio de mínima acción!
Sin entrar demasiado en detalles (es decir, prácticamente ninguno), podemos definir la acción como
.
Al minimizar esa acción, como hicimos en la entrada mencionada anteriormente, obtenemos las ecuaciones de Euler-Lagrange (que, si hay tiempo, serán derivadas en el caso más general en otra entrada):
Si la escribimos de manera explicita:
Esta ecuación es análoga a la segunda ley de Newton si se hubiese podido expresar en la coordenada angular. Y, como ocurría en aquel momento, su solución pasa por las funciones elípticas de Jacobi.
Para demostrar que, en realidad, las ecuaciones del movimiento para el péndulo son las mismas, realicemos la misma aproximación que hicimos en la primera entrada: asumiremos que cerca del punto de equilibrio estable, el péndulo realizará oscilaciones pequeñas. Esto es, .
Bajo estas condiciones, como ya vimos, , y obtenemos desde la última ecuaciones, reorganizando,
Y esta ecuación, en realidad, es exactamente la de un oscilador armónico, pues su solución más general es
Además, la ecuación es, bajo nuestras aproximaciones, idéntica a las obtenidas en la entrada anterior utilizando la Segunda Ley de Newton, pues en estas condiciones, ,
e
¿Es esto sorprendente? En realidad, este resultado solo nos confirma lo que ya habíamos observado en la entrada en que resolvíamos el problema dinámico para el péndulo a la Newton, pero en este caso no hemos tenido que calcular tensiones ni hemos tenido que trabajar con 2 dimensiones espaciales en todo momento.
———————
De este modo, y para concluir esta entrada, hemos obtenido las ecuaciones de movimiento (de Euler-Lagrange) minimizando la acción del sistema, que es una cantidad que depende del Lagrangiano. Esta cantidad, a su vez, depende de las características dinámicas del problema (energía cinética y potencial) y de las restricciones geométricas, pues las variables que utilizamos (en este caso el ángulo ) llevan codificadas las ligaduras del sistema. Esto nos ha llevado a la observación de los grados de libertad y la definición de coordenadas generalizadas. De paso, hemos obviado el cálculo de cantidades accesorias, como las tensiones, mediante el uso de estas coordenadas.
Esto quiere decir que, en vez de tener que calcular las fuerzas que actúan en cada punto y dirección y obtener el equilibrio, podemos suponer que el espacio está “lleno” de un cierto campo (del que se derivan las fuerzas) y que constituye un paisaje en el que nuestro sistema se mueve, como se movería una bolita en un paisaje montañoso: buscando el mínimo.
Sin embargo, y a pesar de que ya podemos derivar las ecuaciones del movimiento mediante un principio de mínimo, no está dicho todo en este tema, y en la próxima entrada de esta serie introduciremos otro método para obtener las ecuaciones del oscilador armónico: la mecánica Hamiltoniana.
Pero eso es otra historia, y deberá ser contada en otro momento…

Muy bien, ahora la idea es hacer un artículo sobre el oscilador armónico visto desde la mecánica cuántica, facil ¿no?.
Hola rosgori.
En efecto, el de la mecánica cuántica llegará, pero quería hacer antes la versión Hamiltoniana.
No es muy diferente al estilo Lagrangiano, pero permite enlazar con la mecánica cuántica más “suavemente” (con menos dolores de cabeza, vaya)
Pingback: Integradores variacionales (Marca ACME) por Fernando Jiménez | Scientia potentia est