La óptica es la rama de la ciencia que se encarga del estudio de la luz en todas sus formas.
Esto no quiere decir, en cualquier modo, que la óptica sea una cosa cerrada: como casi todos los ámbitos de la ciencia, tiene ramificaciones e interconexiones con otras áreas, y es bastante extraño (a menos que estés en la universidad, donde están empecinados en compartimentar todo saber) que se presente aislada, extraña al resto de materias.
Además, tampoco es posible separar completamente cada una de las ramas de la óptica a nivel histórico, pues aunque algunos avances (la óptica cuántica, por ejemplo) sean más modernos, en realidad se puede ver como si fuese un cuerpo del conocimiento al que se han hecho diversas aproximaciones.
Sin embargo, si cambiamos la manera de acercarnos al tema , casi siempre variarán las técnicas utilizadas y la clase de problemas que se pueden tratar dentro de ese marco de referencia.
La siguiente lista, lejos de ser extensiva, es un mero acercamiento a las palabras y los métodos que se utilizan en cada una de las ópticas. Si hay tiempo, escribiré sobre cada una de ellas independientemente, aunque la que más conozco (y de la que más preguntas tengo) es la óptica cuántica.
Óptica geométrica
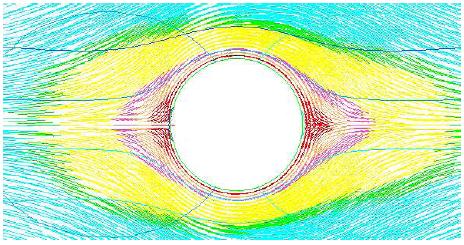
Parte de la idea de que “La luz se transmite en linea recta”. Es la rama más antigua de la óptica, y estudia a un nivel básico, con leyes prácticamente “empíricas” la reflexión y la refracción de las ondas de luz en medios materiales.
Sirve, usualmente, cuando la longitud de onda es muy pequeña en comparación con el resto de distancias en el problema y cuando los ángulos de incidencia a los distintos elementos que atraviesa la luz son pequeños (aproximación eikonal).

Diagrama que muestra como la luz es refractada por un contenedor esférico lleno de agua. (“De multiplicatione specierum”, Roger Bacon, tomada de Wikimedia Commons)
Óptica electromagnética
Surge al estudiar las soluciones de las ecuaciones de Maxwell para el campo electromagnético (PDEs). Por ello, se trata normalmente del estudio de la propagación clásica de ondas armónicas en medios materiales.
Toma la refracción, reflexión y difracción desde el punto de vista microscópico de los materiales. Aparecen las funciones de Green (propagadores) al resolver las ecuaciones de Maxwell. Tiene aplicaciones en ingeniería (telescopios, microscopios,…) , así como en optometría.
Cabe decir que una gran parte de la óptica electromagnética es el estudio de la luz como una “onda” en vez de corpúsculo. Esto ya lo hizo Newton, entre otros sitios, en su “Opticks”
Una de las cosas más interesantes es la aparición de la frecuencia, la amplitud y la polarización en la descripción de las ondas. La fase resulta importante al considerar difracción, aunque también se puede ver en la reflexión y la refracción teniendo en cuenta las condiciones de borde en las ecuaciones de Maxwell.

Birrefrigencia inducida por estrés en plástico. Las franjas coloreadas se hacen visibles cuando se ilumina la muestra con luz polarizada y se fotografía a través de un polarizador cruzado. (Imagen tomada de Wikimedia Commons. Autor: Richard Wheeler)
Óptica estadística
Surge al considerar el campo electromagnético como algo menos “idealizado”: supone distribuciones estocásticas para el campo electromagnético y la emisión de luz como un proceso aleatorio. Esto resulta más correcto cuando hay fenómenos en los que existe coherencia. Estudia fenómenos como la holografía o la interferometría.
La frecuencia y la fase toman un papel fundamental, y se trata de distribuciones de las que uno tiene que obtener “momentos”. La correlación entre puntos del campo EM es importante (al menos hasta segundo orden en intensidad).

Holograma de una paloma en una tarjeta Visa (tomada de la cuenta de Flickr de Dominic Alves)
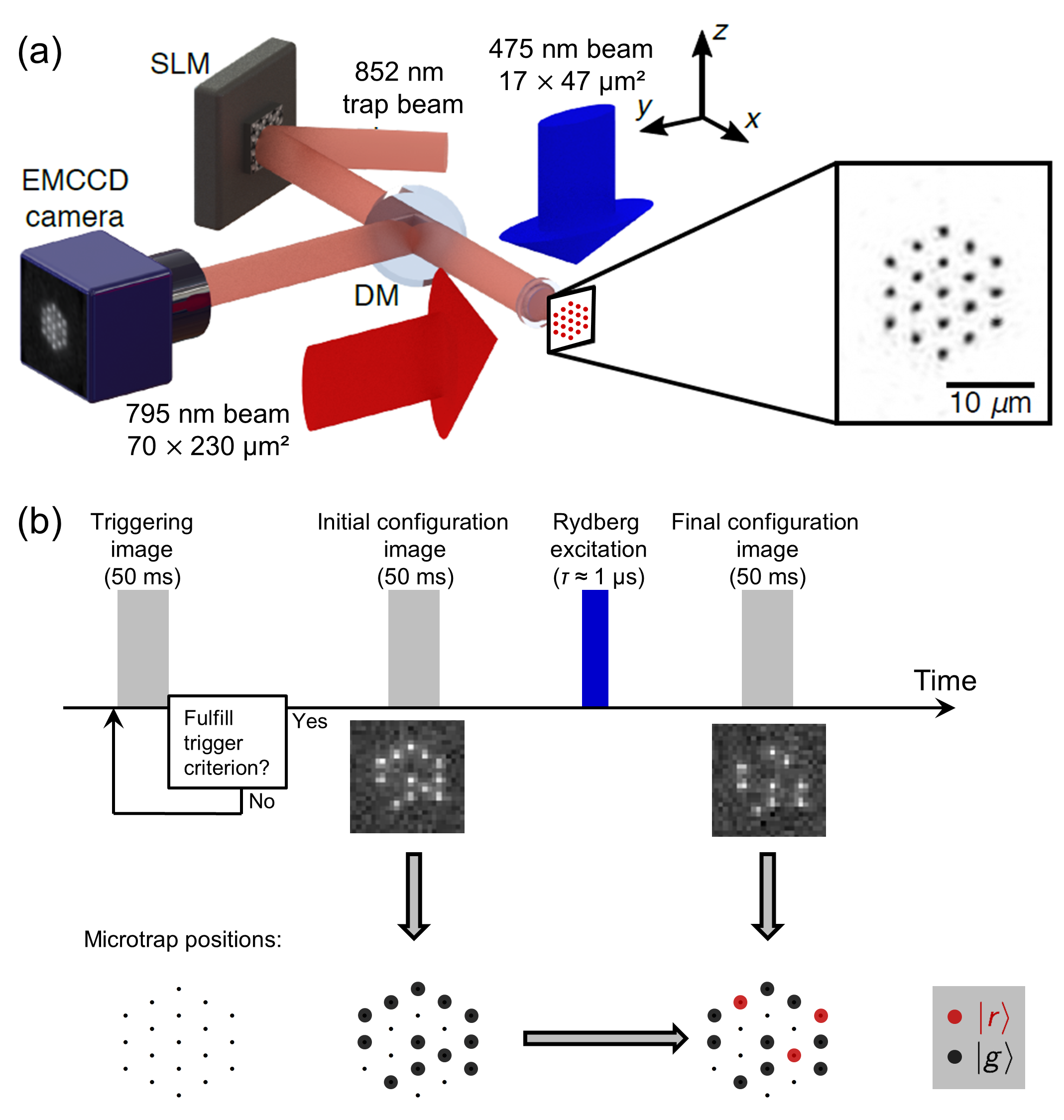
Óptica cuántica
Tanto emisores como receptores tienen características que obedecen a las leyes de la física cuántica. Una de esas características fundamentales es la de la interferencia entre procesos debido a la “indistinguibilidad de las partículas”.
Se utilizan técnicas que van desde las PDEs hasta métodos algebráicos en teoría de grupos (operaciones de creación y aniquilación, momento angular, …). Tiene aplicaciones en espectroscopía, interferometría, … Obviamente, dado que tenemos que describir la propagación en medios que están gobernados por las leyes de la física cuántica, podemos encontrar relación física atómica o con la física de estado sólido y de materia condensada.

Funciones de Wigner de un estado “squeezed”. Estos estados tienen aplicaciones en las medidas que requieren mucha precisión, o bajos niveles de luz, entre otras cosas (Imagen tomada de Wikimedia Commons, originalmente de la tesis de Gerd Breitenbach)