En la anterior entrada hemos hablado un poco de qué es la transparencia inducida electromagnéticamente (EIT) y cómo el medio se puede hacer transparente a luz resonante con frecuencia utilizando luz de otra frecuencia diferente , a la que llamamos “haz de control”. Allí mencionamos que, dentro del medio, esa luz se convierte en una “onda espín”, en una excitación del medio, que depende de la intensidad del haz de control.

En esta segunda entrada, vamos a intentar responder a las siguientes preguntas: ¿Qué es una onda espín? ¿En qué modo depende la onda espín del haz de control? y, por último ¿por qué es esto tan relevante para la computación cuántica?

Para los mas avezados lectores existe “el articulo de referencia” [1] (en inglés) que es un poco técnico, pero es un compendio bastante completo sobre la fenomenología asociada con el EIT.

¿Qué es una onda espín?

Una onda espín es una medida de como los electrones en los átomos de un medio reaccionan como resultado de la aplicación de un campo electrico (la luz), a lo que llamamos la polarización del medio. En un material como el que nos ocupa, es una “coherencia” entre los niveles A y C.

Se le llama “onda” porque se propaga, y el apósito “espín” tiene que ver con el hecho de que, al conectar los dos niveles A y C, esta excitación se puede describir como si hablásemos de un material magnético con un cierto espín.

Un pulso de luz que entra en el medio hace que el medio se polarice: los electrones en los átomos se alinean con el campo eléctrico del pulso.

Sin embargo, en general, cuando la luz se propaga en el medio, lo hace como una mezcla entre fotón y onda espín. El nombre más común para esta mezcla es “polaritón de estado oscuro” (dark state polariton). El nombre “polaritón” es solo una invención (al igual que onda espín), pero tienen la particularidad de que esa mezcla concreta de fotón y onda espín se comporta como un bosón. La característica más importante de los bosones es que si tienes varios de ellos, todos pueden ocupar el mismo estado – esto es, se pueden “apelotonar” unos encima de otros – al contrario de lo que ocurre con los fermiones, que no pueden tener el mismo estado – que es lo que se llama el principio de exclusión de Pauli.

¿En qué modo depende la onda espín del haz de control?

La proporción de “fotón” y la proporción de “onda espín” depende de la cantidad de luz del haz de control.

Si el haz de control es muy potente, casi todo el polaritón es “fotón”, mientras que si es débil, casi todo el polaritón será onda espín.

Imaginemos que la intensidad del haz de control fuese 0 todo el rato. Entonces, como la luz f1 es resonante sería absorbida por el medio, y no veríamos nada a través de él (sería opaco). Si encendemos el haz de control, entonces cuando los fotones se propagan, se transforman en parte en onda espín. Entonces, si apagamos el haz de control, el resto, que se estaba propagando en el interior, se transforma en onda espín, siendo almacenado. Después, cuando encendemos el haz de control de nuevo, siguen propagándose hasta que salen del medio, y recuperamos los fotones .

Pero de la intensidad del haz de control también depende la velocidad del polaritón, como dijimos en la entrada anterior.

Si el haz de control es muy potente, al ser casi todo luz, se propaga rápido, y si es débil, se propaga lento, hasta detenerse cuando no queda luz.

Esto quiere decir que, cuando estamos apagando el haz de control, los polaritones que se están propagando por el medio se van frenando hasta detenerse cuando el haz de control está apagado. Luego, cuando se vuelve a encender, los polaritones se aceleran, y se siguen propagando por el medio hasta que salen de este.

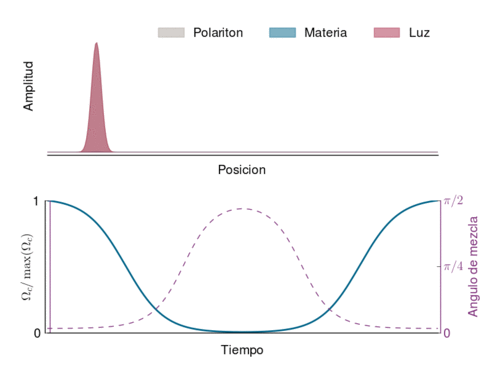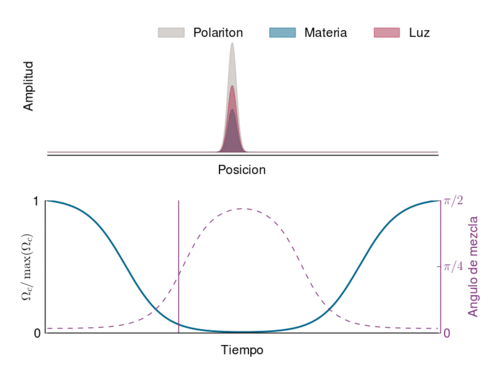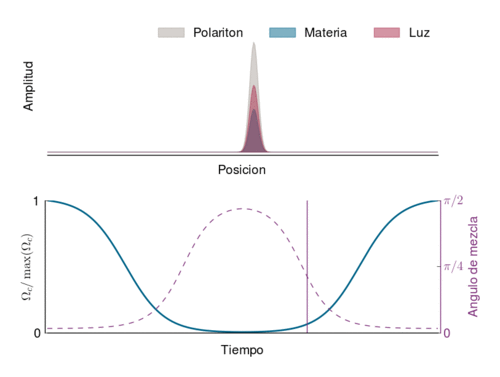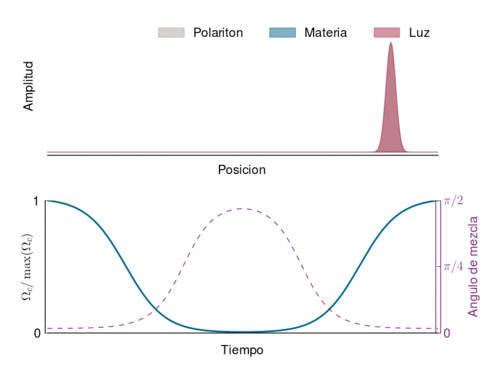
Cuando está dentro del medio, las caracteristicas del polaritón dependen de la intensidad del haz de control (linea azúl en el gráfico de abajo): cuando se hace más débil, la proporción de onda espín (materia) aumenta  y la velocidad disminuye (hasta pararse cuando se apaga el haz de control). Y viceversa. El ángulo de mezcla mide la proporción de onda espín y de fotón en el polaritón.

¿Cuál es la relevancia para la computación cuántica?

En un cierto sentido, podemos imaginar los componentes de la computación cuántica (QC) como si fuesen los de la computación clásica: para realizar cálculos necesitamos necesitamos una manera de guardar la información (memoria), una manera de llevarla de un sitio a otro (canal), y una manera de hacer calculos (procesado).

En el caso de la computación clásica, la información se suele guardar en unidades llamados “bits” que codifican en alguna propiedad física los estados “0” o “1” del sistema. Usualmente, estos pueden ser codificados como “el voltaje entre estos nodos es 0” o “es distinto de 0”, o “la orientación del material magnético es hacia arriba” o “hacia abajo”…

Pero, en el caso de la QC la información es de una naturaleza distinta, así que la debemos codificar en modo diferente, cuántico. Las memorias “clásicas” no sirven para guardar esa información, dado que no solo hay que guardar “0” o “1”, sino una superposición arbitraria de ellos, llamados “qubits”. Además, podemos encontrar correlaciones entre estos qubits que no pueden ser descritos con la física clásica. Esto es lo que se llama “entrelazamiento cuántico”. El problema es que estas superposiciones y el entrelazamiento son muy frágiles: cualquier tipo de fluctuación puede afectarlas, haciendo que parte de la información se pierda.

Es ahí, en la parte de “guardar la información”, en el que este tipo de avances tienen más importancia: si consigues guardar esa información de carácter cuántico por bastante tiempo sin que pierda sus propiedades, puedes utilizarla más tarde para procesarla, o puedes guardar grandes cantidades de información para utilizarla en procesos subsiguientes, y hacer computaciones más complicadas con ella.

[1] Fleischhauer, Imamoglu y Marangos, ” Electromagnetically induced transparency: Optics in coherent media” Rev. Mod. Phys. 77, 633–673 (2005) (o de acceso libre)