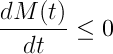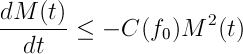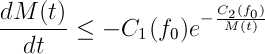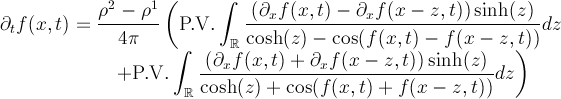Problemas de frontera “no-tan-libre”

Posted on 07/11/2012 by el guacho

Resulta que en el Instituto de Ciencias Matemáticas hay un “Working Pizza Seminar“, (además del enlace “oficial” aquí se puede ver el enlace al blog del ICMAT) es decir, un sitio donde se dan charlas informales sobre temas de investigación actual y, además, te dan pizza para comer, y hoy he ~~torturado~~ hablado yo.

He hablado un poco de las cosas que he estado haciendo estos casi 3 años que llevo con la tesis (ver las diapositivas aquí PizzaWorkingSeminar). Es decir, he tratado problemas de frontera libre que surgen en el movimiento de fluidos incompresibles en medios porosos inhomogéneos. Así, por ejemplo, he explicado entre otras cosas, cuándo este tipo de olas puede tener singularidades

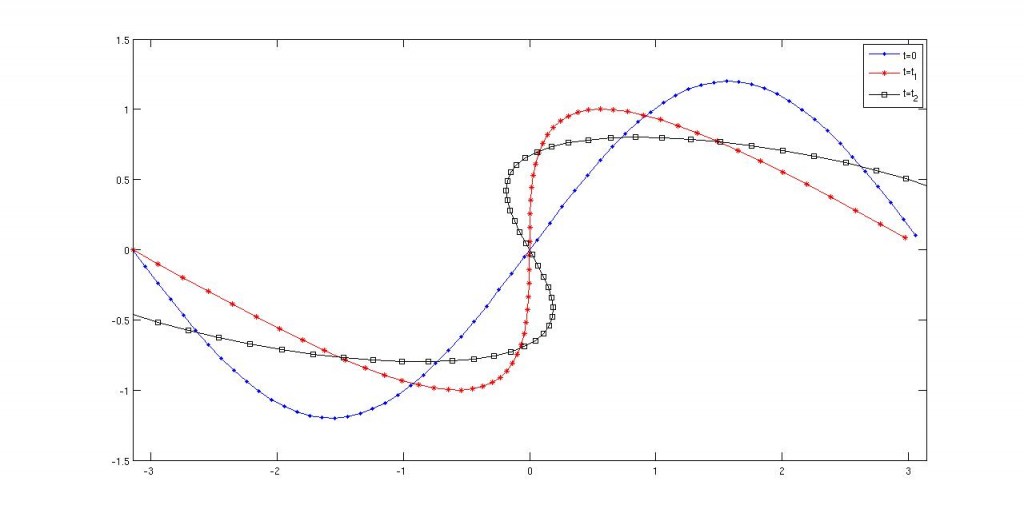
Y también cuando es de esperar que no.

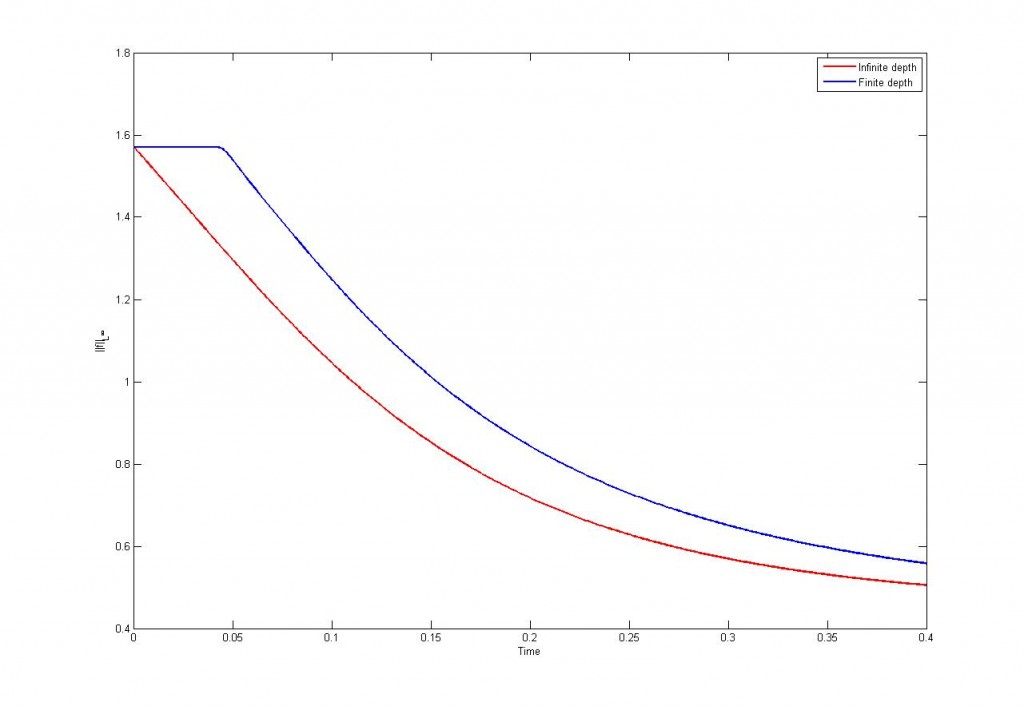
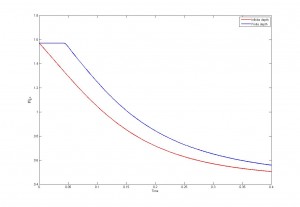
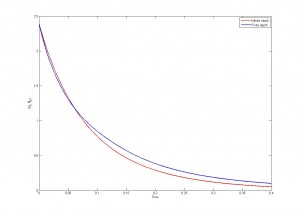
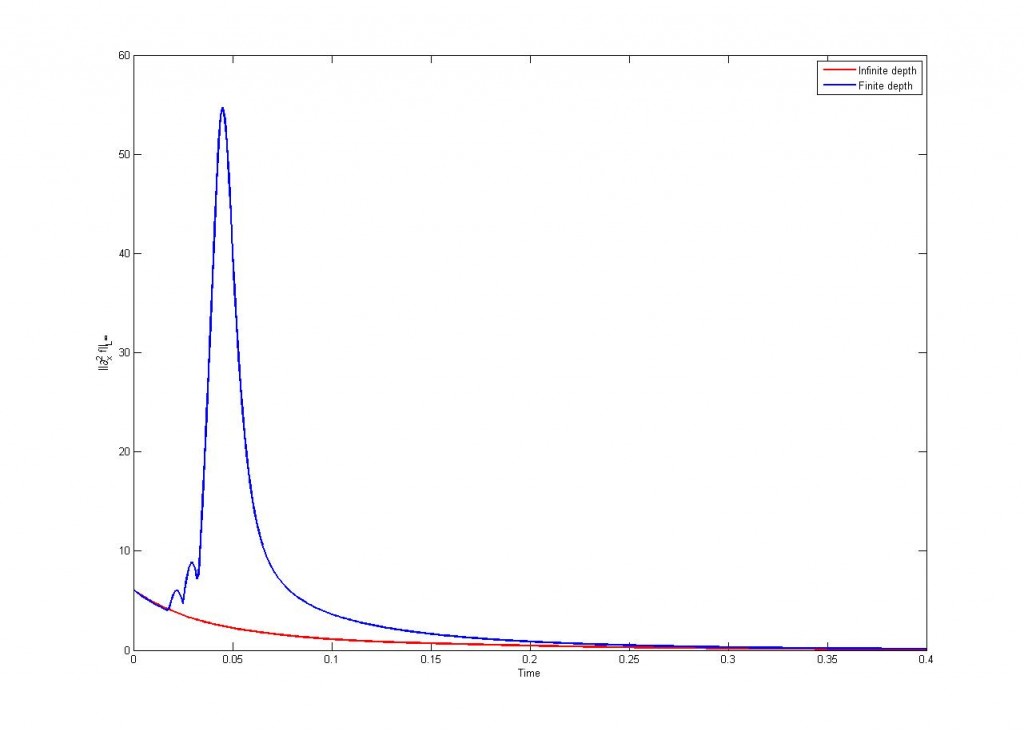
Además he comparado diversos modelos existentes. Por ejemplo he comparado el caso homogéneo con profundidad infinita con el caso homogéneo con profundidad finita (puede argumentarse que las fronteras del dominio serían zonas de permeabilidad nula y por lo tanto el problema sería inhomogéneo… pero dejémoslo estar)

También he comparado casos con distinta permeabilidad

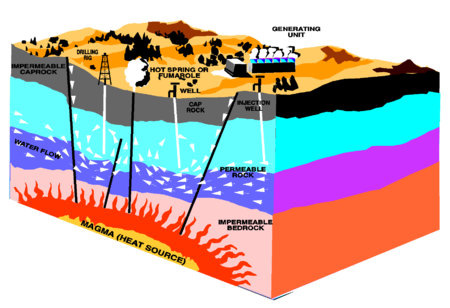
Todos estos problemas son interesantes, por ejemplo, de cara a la obtención de energía. En efecto, si uno quiere extraer petróleo lo que se suele hacer es inyectar agua a presión de manera que ésta lo desplaza, expulsándolo (ver aquí). Otra fuente de energía, esta vez mucho menos conocida, es la energía geotérmica (ver aquí). Ahí típicamente se tiene una zona de permeabilidad altísima, una de permeabilidad más normal y ambas se encuentran acotadas por capas impermeables. Ahí se tiene que el agua está muy caliente debido al calor propio del núcleo de la Tierra y por lo tanto puede aprovecharse para obtener electricidad.

–Nota: La portada hay que agradecérsela a Elena Hontangas Martínez

–Nota 2: Parece mentira la cantidad de cuadros que hay dedicados exclusivamente a las olas. Será la única cosa que tengan en común matemáticos y artistas en sus respectivos trabajos…

Problemas de frontera “no-tan-libre” en dinámica de fluidos: las diferencias

Posted on 25/09/2012 by el guacho

En esta entrada tratamos de presentar de manera sencilla la siguiente pregunta

¿Cómo de importante es el lecho marino para las olas en la superficie?

Así tenemos que estudiar el problema de la evolución de la interfase entre dos fluidos cuando dichos fluidos se encuentran en un medio poroso acotado y, tras hacer unas simulaciones para ver por dónde iban los tiros, dimos los primeros pasos en el estudio matemático del problema. Sin embargo, pese a que en las simulaciones observamos grandes diferencias en los primeros resultados matemáticamente rigurosos no capturamos esos fenómenos.

La primera pregunta que nos hacemos es ¿cuál es la evolución de la amplitud máxima de la ola? Para ellos lo que hacemos es estudiar

Lo que conseguimos probar es

o, lo que es lo mismo, que la amplitud no puede crecer con el tiempo. Este resultado es idéntico al caso donde la profundidad es infinita. Sin embargo en las simulaciones habíamos visto que las diferencias a este nivel eran grandes:

Lo que ocurre es que la velocidad a la que cae la amplitud es distinta. En el caso de profundidad infinita tenemos

donde $f_0(x)=f(x,0)$ es la ola inicial. En el caso de un medio acotado la amplitud evoluciona según

Así hemos obtenido la primera diferencia importante: la interfase en el caso de profundidad finita decae más despacio.

Ahora cabe preguntarse ¿cómo evoluciona $\max_x|\partial_x f(x,t)|$ ? Esta cantidad nos da una idea de cómo es la longitud de onda. Sabemos que en el caso donde el medio no está acotado se tiene que

si $\max_x|\partial_x f(x,0)|<1$ entonces $\max_x|\partial_x f(x,t)|<\max_x|\partial_x f(x,0)|\;\; \forall t>0.$

En el caso de que el medio tenga profundidad finita tenemos una condición (razonablemente complicada y que escribiremos $F$ ) que involucra no sólo a $\max_x|\partial_x f(x,0)|$ si no también a $\max_x|f(x,0)|$ :

si $F(\max_x|\partial_x f(x,0)|,\max_x|f(x,0)|)\leq 0$ entonces $\max_x|\partial_x f(x,t)|\leq\max_x|\partial_x f(x,0)|\;\; \forall t>0.$

Una consecuencia de esto es que si esa condición se satisface y entonces tenemos una cota superior para $\max_x|\partial_x f(x,t)|$ y por lo tanto la ola no puede romper.

Bueno, ahora que sabemos cuándo la interfase no rompe cabe preguntarse si hay alguna situación en la que la interfase rompa. Y efectivamente obtenemos que hay datos tales que pasa lo siguiente:

Es más, podemos probar mediante una prueba asistida con ordenador, que existen datos iniciales tales que sólo rompen cuando la profundidad es finita. Es decir, que el fondo ayuda a que las olas rompan. Y si bien hemos probado estos teoremas en el caso de fluidos moviéndose en un medio poroso estos dos últimos resultados se pueden probar gratis para el caso de las water waves, i.e. la interfase entre un fluido incompresible e irrotacional siguiendo las ecuaciones de Euler y el aire.

–Referencias:

D. Córdoba, RGB, R.Orive, The confined Muskat problem: differences with the deep water regime.

–Nota: Con esta entrada participamos en el Carnaval de Matemáticas en su edición 26, organizado esta vez por ZTFNews.

–Nota 2: Con esta entrada participamos también en el Carnaval de Física en su edición XXXIV que organiza Hablando de Ciencia.

Problemas de frontera “no-tan-libre” en dinámica de fluidos: primeros pasos

Posted on 24/09/2012 by el guacho

Decía el señor Swett Marden que

“Un guijarro en el lecho de un pobre arroyuelo puede mudar el curso de un río”.

Parece una exageración y sin duda lo es, pero sirve para que nos hagamos la siguiente pregunta:

¿Cómo de importante es el lecho marino para las olas en la superficie?

Ésta es la pregunta que tratamos de contestar en este artículo. El problema que queremos entender es, dados dos fluidos incompresibles en un medio poroso acotado, ¿cómo se comporta la interfase entre ambos y que diferencias presenta con el caso en el que el medio no esta acotado? Bueno, vamos a trasladar ese problema físico a ecuaciones en derivadas parciales. Tenemos una densidad que presenta dos valores según estemos por encima o por debajo de la interfase, que denotamos por ,

Que los fluidos sean incompresibles y se muevan en un medio poroso acotado quiere decir que el dominio espacial de los fluidos es

y que la velocidad satisface la Ley de Darcy y la condición de incompresibilidad

Estas ecuaciones se puede trasladar a una única ecuación para la interfase:

Ahora que tenemos el problema cabe preguntarnos si el hecho de que el dominio sea $S$ y no $\mathbb{R}^2$ cambia mucho la situación. Para hacernos una idea podemos hacer unas simulaciones numéricas preliminares. Para ello consideramos un dato inicial y lo hacemos evolucionar en el caso donde el medio tiene profundidad finita (caso acotado) y también en el caso en el que el medio tiene una profundidad infinita (caso no acotado). Por supuesto el resto de los parámetros físicos son los mismos en ambas evoluciones. Así observamos lo siguiente

(Si no ves bien las imágenes pincha en ellas para hacerlas más grandes)

Parece claro a la vista de estos resultados que el hecho de que el medio esté acotado o no es relevante para las olas.

Una vez que tenemos el problema propuesto tenemos que empezar a sacar teoremas :-P. Evitando tecnicismos lo primero que probamos es

1) (Existencia y unicidad) que si el fluido de arriba es más ligero que el que está abajo el problema tiene una solución.

1.b) (Existencia y unicidad 2) que si el fluido de arriba es más pesado que el de abajo pero la interfase inicial es analítica existe una solución.

2) (Efecto regularizante) que dicha solución se vuelve muy regular (analítica) para cualquier $t>0$ (compárese con la ecuación del calor aquí.)

De momento estos 3 teoremas son idénticos en su enunciado a los teoremas cuando la profundidad es infinita. ¿Sorprendido? Bueno, esto sólo quiere decir que para probar matemáticamente las diferencias que hemos visto en los vídeos y las imágenes anteriores tenemos que trabajar un poco más, así que sed pacientes y esperad a la siguiente entrada ;-).

Bueno, si os veis muy impacientes podéis leer (o, en su caso, releer) ésta, ésta y esta entrada.