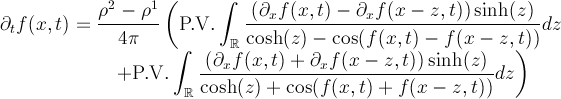En esta entrada hacemos una breve revisión de un tema que nos parece muy interesante: el efecto que tiene la bacteria wolbachia en unas subespecies particulares de saltamontes, Chorthippus parallelus parallelus y Chorthippus parallelus erythropus. La distribución de estos animalejos se solapa en los Pirineos, donde forman una zona híbrida (ZH), es decir, una región donde individuos de las dos subespecies se encuentran, se cruzan y dan lugar a descendencia híbrida, en aquellos puntos en los que la orografía y sus requerimientos ecológicos lo permiten. Esta ZH responde a un contacto secundario entre poblaciones endémicas ibéricas (Cpe) y de la Europa continental (Cpp), que se expandieron después de la última glaciación desde aquellos refugios en los que habían divergido genéticamente en alopatría, esto es, especiación por aislamiento geográfico.
Las diferencias morfológicas, fisiológicas, genéticas y de comportamiento entre estas subespecies (y sus híbridos naturales y de laboratorio) han sido intensamente estudiadas en estos últimos años, por lo que esta ZH se considera un modelo singular en Biología Evolutiva (Bella et al., 2010). Estos estudios muestran un escenario complejo, con un número considerable de causas involucradas en el origen, estructura y mantenimiento de dicha ZH y ofrecen una muy buena panorámica de la evolución “en acción”. ¡Por esto es importante e interesante!
Por otra parte, Wolbachia es una bacteria endosimbionte obligada (esto es, sin palabras de brujo, que vive exclusivamente en el interior de las células del insecto al que infecta) que induce alteraciones en la reproducción de diversos organismos, fundamentalmente artrópodos y nematodos. Esta bacteria induce, por ejemplo, feminización de los machos o incluso su muerte selectiva. También producen incompatibilidad citoplasmática que consiste en la incapacidad de un macho infectado de tener descendencia con una hembra que no esté infectada (Serbus et al., 2008). Esto condiciona los cruzamientos entre poblaciones infectadas en distintos grado por esta bacteria, lo que se ha planteado como un posible ejemplo de “especiación por infección” (Wade, 2001).
En estudios previos hemos profundizado en la Biología de este microrganismo y hemos comprobado que en la ZH de Chorthippus genera una barrera reproductiva considerable (Zabal-aguirre et al., 2010; Bella et al., 2010), lo que apunta a que, efectivamente, esta bacteria puede promover fenómenos de especiación.
Debido a su peculiar forma de transmisión, de madres a hijos, la dinámica de la infección por Wolbachia es compleja. A su vez la forma por la cual la infección pueda condicionar los cruzamientos que se producen en una población y sus repercusiones a largo plazo son dificiles de estudiar en el laboratorio. Más aun en condiciones naturales. Es por esto. que la infección por Wolbachia ha sido modelizada matemáticamente (¡aquí aparece la caballería!) con el fin de conocer hasta qué punto esta bacteria influye en las poblaciones a las que infecta (Turelli et al., 1994; Telschow et al., 2005; 2007; Vautrin et al., 2007).
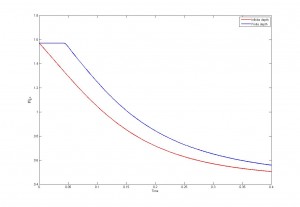
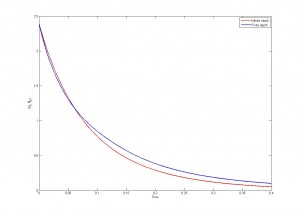
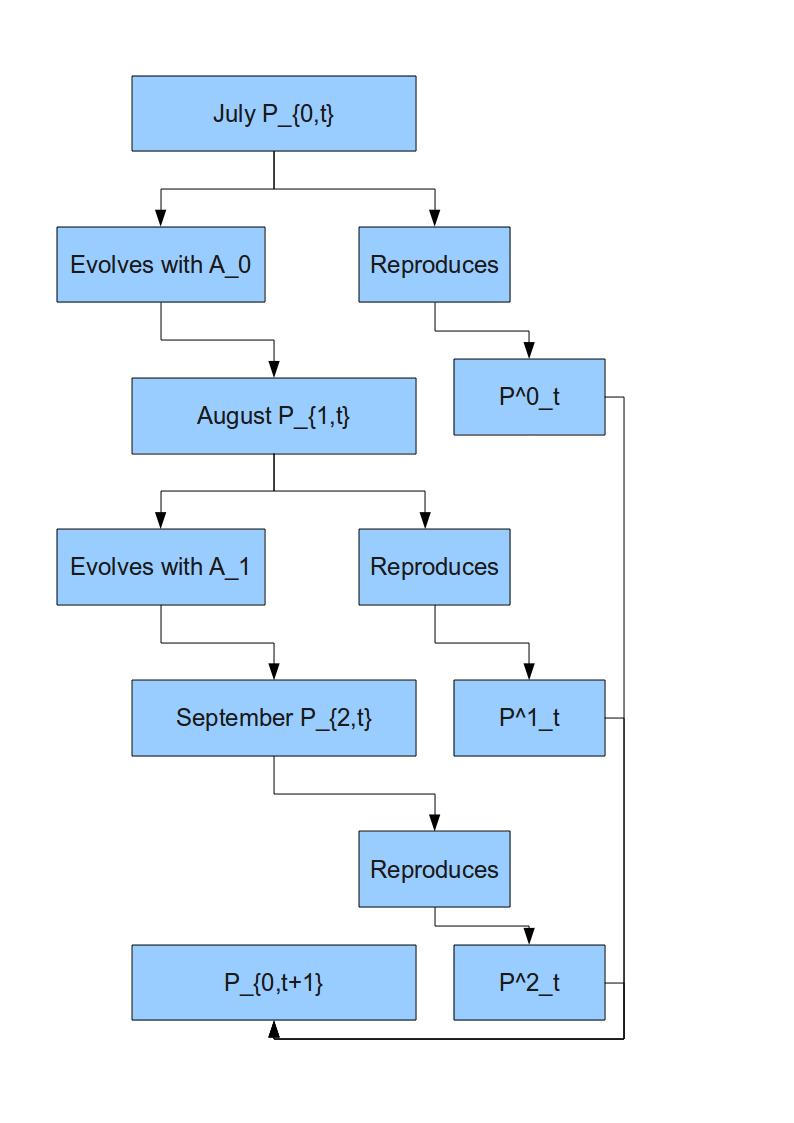
Bien, hasta aquí el tema y la historia que hay detrás, pero ¿qué hemos hecho nosotros? Pues hemos continuando con los estudios de Vautrin et al. (2007), implementando una variante de este modelo para analizar (i) cómo podría evolucionar la infección por Wolbachia en una población modelo de Chorthippus parallelus y por otra parte (ii) cómo influirían algunas variables ambientales, por ejemplo la temperatura, en la dinámica de la infección. Nuestro modelo sigue el siguiente esquema
Como nos está quedando un poco largo ya, vamos a concluir con la referencia del trabajo por si alguien está interesado en abundar más:
Wolbachia infection in Chorthippus parallelus: Intra-generational frequency variation, P. Martínez-Rodríguez, R. Granero-Belinchón, F Arroyo-Yebras y J.L. Bella. (aquí hay un poster sobre este tema).
Referencias:
- Bella JL, Martínez-Rodríguez P, Arroyo-Yebras F, Bernal A, Sarasa J, Fernández-Calvín B, Mason PL & Zabal-Aguirre M. 2010. Wolbachia infection in the Chorthippus parallelus hybrid zone: evidence for its role as a reproductive barrier. Journal of Orthoptera Research 19 (2): 205-212
- Hewitt G. 2000. The genetic legacy of the Quaternary ice ages. Nature 405, 907-913.
- Serbus LR, Casper-Lindley C, Landmann F, Sullivan, W. 2008. The genetics and cell biology of Wolbachia-host interactions. Annu Rev Genet 42: 683-707.
- Telschow A, Flor M, Kobayashi Y, Hammerstein P, Werren JH. 2007. Wolbachia-induced unidirectional cytoplasmic incompatibility and speciation: mainland-island model. PLoS ONE Aug 8; 2(1):e701.
- Telschow A, Hammerstein P, Werren JH. 2005. The effects of Wolbachiaversus genetic incompatibilities on reinforcement and speciation. Evolution 59: 1607-1619.
- Vautrin E, Charles S, Genieys S, Vavre F. 2007. Evolution and invasion dynamics of multiple infections with Wolbachiainvestigated using matrix based models. J Theor Biol. 245(2):197-209.
- Wade MJ. 2001. Infectious speciation. Nature, 409: 675-677.
- Zabal-Aguirre M, Arroyo F & Bella JL. 2010. Distribution of Wolbachia infection of Chorthippus parallelus in populations within and beyond a Pyrenean hybrid zone. Heredity 104: 174–184.
–Nota: Con esta entrada participamos en el Carnaval de Biología en su décima edición organizado por Scientia y en el de Matemáticas, que organizamos nosotros.
y no 
cambia mucho la situación. Para hacernos una idea podemos hacer unas simulaciones numéricas preliminares. Para ello consideramos un dato inicial y lo hacemos evolucionar en el caso donde el medio tiene profundidad finita (caso acotado) y también en el caso en el que el medio tiene una profundidad infinita (caso no acotado). Por supuesto el resto de los parámetros físicos son los mismos en ambas evoluciones. Así observamos lo siguiente
(compárese con la ecuación del calor