En esta nueva entrada de la serie de las paradojas (las primeras estradas son http://scientiapotentiaest.ambages.es/?p=244 y http://scientiapotentiaest.ambages.es/?p=266) nos vamos a centrar en las paradojas que vienen de la probabilidad. Y es que la probabilidad pese a ser algo bastante mencionado en la vida diaria no es entendida por mucha gente.
Voy a comenzar tratando el problema de Monty Hall. Este problema es muy divertido, porque todo el mundo al que se lo contemos dirá que es muy intuitivo. ¡El problema es que para cada uno será intuitiva una respuesta distinta!
Supongamos que estamos en un programa de estos de la tele. En este programa hay tres puertas. Una de las tres tiene un premio y las otras dos no tienen nada. La puerta que tiene el premio se elige al azar de manera equiprobable. El juego consiste en elegir una puerta. Tras nuestra elección, el presentador, que sabe dónde está el premio, abre una de las dos puertas que no hemos elegido y que no tiene nada. Tras esto nos pregunta si queremos cambiar de puerta. La pregunta viene ahora, ¿qué nos sale mejor como jugadores? ¿cambiar nuestra primera elección o dejarla estar?
Observamos que el premio no cambia de puerta mientras nosotros jugamos.
La respuesta correcta es que siempre nos sale mejor cambiar de puerta. Sí, amigos lectores, es mejor cambiar. ¿Qué no me creéis? Vamos a ver si os convenzo. Como el premio está en una de las puertas de manera equiprobable la probabilidad de que el premio se encuentre en la puerta que hemos elegido al comenzar a jugar es 1/3. Ahora el presentador abre una de las otras dos puertas sin descubrir el premio. ¿Cuál es la probabilidad de que nuestra puerta esconda el premio? LA MISMA, 1/3. Por lo tanto si cambiamos de puerta nuestra nueva elección tendrá probabilidad 2/3. Vamos a ilustrar esto un poco más mirando los posibles casos. Vamos a suponer que elegimos siempre la puerta 1, como todo es simétrico todos los casos estarán reflejados igualmente.
1) El coche está en la puerta 1.
1.a) Cambiamos de puerta y perdemos.
1.b) No cambiamos y ganamos.
2) El coche está en la puerta 2.
2.a) Cambiamos de puerta y ganamos.
2.b) No cambiamos y perdemos.
3) El coche está en la puerta 3.
3.a) Cambiamos de puerta y ganamos.
3.b) No cambiamos y perdemos.
Hagamos el recuento: Si cambiamos ganamos 2 veces frente a una que perdemos. Si no cambiamos la situación es recíproca. Como hay 3 casos posibles la probabilidad de ganar cambiando es 2/3.
Otra manera de convencerse es aumentar el número de puertas. Supongamos que tenemos 100 puertas. Entonces la probabilidad de que el premio esté en nuestra puerta es 1/100. Tras elegir, el presentador abre todas las puertas menos dos, la que tu elegiste y otra, de manera que ninguna de las abiertas mostrase el premio. Ahora parece claro que lo mejor es cambiar.
Otra paradoja que invariablemente se estudia en los cursos iniciales de probabilidad es la paradoja de los hijos (a falta de un nombre mejor en castellano). Supongamos que la probabilidad de que nazca un chico o una chica es la misma, 50%, y que el sexo de cada hijo es independiente del sexo de los demás hermanos. Vamos con el problema. La señora López tiene dos vástagos. Supongamos, a modo de calentamiento, que el hijo mayor de la señora López es un niño, ¿cuál es la probabilidad de que el menor sea niña? La respuesta, claro, es 50%. Ahora se nos plantea un problema ligeramente distinto: Supongamos que uno de los hijos de la señora López es niño, ¿cuál es la probabilidad de que el otro hijo también sea niño? ¿50%? Veamos los casos tal cuál está escrito (observando que la familia está fija para los más puntillosos) y ordenando los niños por edad:
1) Chico-chico
2) Chica-chico
3) Chico-chica
Hay 3 casos posibles y sólo 1 es el que nos preguntan. Como son equiprobables la probabilidad de que ambos hijos de la señora López sean niños es 1/3. El truco aquí está en que al decir que uno de los hijos es chico perdemos información sobre su edad. En la primera pregunta tenemos más información y podemos descartar más casos.
La probabilidad se va descubriendo un poco farragosa y “extraña” en ocasiones. Sin embargo todavía no hemos tratado la principal fuente de problemas al tratar con la probabilidad. Me refiero a la ambigüedad. Las palabras “al azar” no tienen un significado preciso y se usan con más asiduidad de la recomendable. Esto quedó claramente expuesto en la obra de J. Bertrand “Calcul des probabilités”. En este manual propuso un enunciado y dio varias respuestas al problema, todas bien lógicas y correctas. El problema era que en cada uno la definición de “al azar” era distinta. Es ahora cuando nos ponemos técnicos. En la entrada anterior ya mencionamos cosas como “medidas” de conjuntos (ver la entrada anterior). Eso nos volverá a ser útil, pues la manera matemática de dar sentido a las palabras “al azar” utiliza esas ideas. En matemáticas un “espacio de probabilidad” es un espacio de sucesos posibles en nuestro experimento, una manera de agruparlos en conjuntos y una manera de “medir la probabilidad” cada uno de estos conjuntos de sucesos. Claro está que la definición precisa es mucho más técnica. Así la idea que quiero dejaros es que esas tres cosas abstractas es lo que da sentido a la palabra “azar”.
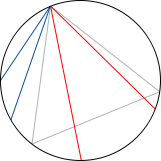
El ejemplo que más me gusta de esto es la paradoja de Bertrand. Consideremos un círculo con un triángulo equilatero inscrito. La pregunta ahora es ¿cuál es la probabilidad de que una cuerda trazada “al azar” sea más larga que los lados del triángulo? Veamos las tres maneras clásicas de calcular dicha probabilidad:
1) Supongamos, sin pérdida de generalidad, que uno de los extremos de la cuerda coincide con uno de los vértices del triángulo. En ese caso al quedar la circunferencia dividida en 3 trozos iguales y coincidir uno con el conjunto donde la cuerda es más larga que el lado del triángulo concluimos que la probabilidad pedida es 1/3. Aquí el espacio de sucesos es el conjunto de puntos de la circunferencia y la medida de probabilidad asociada es la longitud del arco considerado dividido la longitud total de la circunferencia.
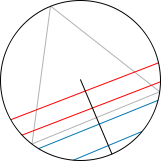
2) Consideremos ahora un radio perpendicular a uno de los lados del triángulo. Esto de nuevo nos facilita la vida pero no perdemos generalidad. Ahora trazamos la cuerda de manera perpendicular a dicho radio por un punto aleatorio del mismo. La probabilidad de que la cuerda sea mas larga que el lado es justamente 1/2 si la trazamos con estas reglas. Aquí el espacio de sucesos es el conjunto de puntos del radio y la medida de probabilidad es la longitud del segmento considerado dividido por la longitud total.
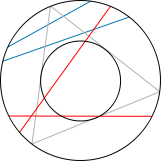
3) Ahora nuestro experimento consiste en elegir el punto medio de la cuerda. Si trazamos la cuerda con esta regla la probabilidad de que la longitud de la cuerda sea mayor que la del lado del triángulo es la misma que la probabilidad de que el punto medio de la cuerda esté en un círculo concentrico inscrito en el triángulo de radio la mitad (y área 1/4 del área del círculo original). Por lo tanto la probabilidad será 1/4. Aquí el espacio de sucesos es el conjunto de puntos del círculo y la medida de probabilidad es el área del conjunto de puntos considerado dividido entre el área del círculo original.
La paradoja aquí estriba en que para una pregunta tenemos tres respuestas. Además, eligiendo la definición de “azar” todas son correctas.
Creo que ha quedado claro que cuando decimos cosas como “aleatorio” o “al azar” no estamos en realidad diciendo nada y que debemos entrar, aunque no queramos, en tecnicismos para evitar este tipo de paradojas.
— Nota: Las imágenes han sido obtenidas de la Wikipedia en inglés
— Nota: Con esta entrada participamos en el Carnaval de Matemáticas en su edición 2.6 (albergado por “La vaca esférica” , http://lavacaesferica.com/).
Esta entrada es la gemela de la entrada Introducción al cálculo variacional en la física (http://scientiapotentiaest.ambages.es/?p=87). En ella David nos decía
Queremos saber qué camino tomará un cuerpo en una cierta situación. Imaginemos que tenemos una cantidad (un funcional, matemáticamente hablando), a la que llamaremos acción (con unidades de energía por segundo), que depende del “camino” que ese cuerpo toma en su movimiento. Esa acción puede ser calculada para cada cualquier camino siempre y cuando tenga una cierta regularidad. Pues bien, el camino real, el que tomará el cuerpo y que podrá ser predicho, es aquel que hace de la acción un mínimo (más rigurosamente, un valor estacionario).
Así, el enfoque en mecánica clásica es: dado un sistema físico, obtenemos un funcional; a este funcional se le calculan los puntos críticos y esos puntos críticos nos dan las soluciones del problema. Matemáticamente esto es ir del funcional a la ecuación diferencial.
Veamos esto con un ejemplo: Supongamos que tenemos una partícula de masa unidad bajo el influjo de un potencial 
Entonces el Lagrangiano se define como
donde 
Ahora definimos la acción como ![A[x]=\int_0^t L(x)dt.](https://s0.wp.com/latex.php?latex=A%5Bx%5D%3D%5Cint_0%5Et+L%28x%29dt.&bg=T&fg=000000&s=0 "A[x]=\int_0^t L(x)dt.")
Una vez tenemos la acción, queremos minimizarla. Para esto hemos de encontrar los puntos críticos. Si fuese una función de una variable normal y corriente derivaríamos e igualaríamos a 0. Derivar es encontrar el cambio de una cantidad cuando se varía otra de manera infinitesimal. Aquí la idea es similar. Lo que hacemos es, dada una perturbación con los extremos fijos (
Ahora pensamos la acción para esta nueva curva 
=\int_0^t L(y(t))dt](https://s0.wp.com/latex.php?latex=A%5By%5D%28s%29%3D%5Cint_0%5Et+L%28y%28t%29%29dt&bg=T&fg=000000&s=0 "A[y](s)=\int_0^t L(y(t))dt")
y obtenemos el cambio en ella cuando variamos ligeramente s; esto es, derivamos en 
Calculamos, utilizando la regla de la cadena,
Sustituyendo obtenemos 
Esta integral debe ser 0 para que nuestra 
Estas consideraciones nos imponen una relación entre las derivadas 
que es, nada más y nada menos, la segunda ley de Newton.
Este enfoque va desde el funcional, que se obtiene con consideraciones físicas, a la ecuación diferencial. O de otra manera, se usa una ecuación diferencial para solucionar un problema de minimizar un funcional.
Sin embargo también existe el método inverso. Supongamos que tenemos una ecuación diferencial (generalmente en derivadas parciales) como puede ser
con 
Demostrar la existencia de solución para la ecuación original es lo mismo que conseguir un punto crítico de nuestro funcional. Si además probamos que es único entonces la ecuación tendrá una única solución. Así con este enfoque vamos desde la ecuación al funcional.
Y como seguir abundando en este tema puede ser muy técnico lo dejaremos aquí por el momento.
El Viernes pasado estuve en la conferencia “SERIES LÓGICAS Y CRÍMENES EN SERIE” de Guillermo Martínez, el autor de “Crímenes imperceptibles” (que es la novela en la que se basa la película “Los crímenes de Oxford”. La presentadora de la conferencia fue Rosa Montero y estaba organizada por el Instituto de Ciencas Matemáticas (que es donde trabajo).
La presentación del conferenciante no me gustó mucho. Creo que la señora Rosa Montero transmitió una serie de tópicos sobre los matemáticos que se pueden resumir en la siguiente frase, que cito textualmente,
“Tener un amigo matemático es como tener un amigo trapecista: exótico.”
La conferencia en sí no estuvo mal… No eran matemáticas y sospecho que este tipo de charlas divulgativas tienen un efecto contraproducente, pero Guillermo Martínez lo contó muy bien y ameno. En general pienso que este tipo de charlas hace que la gente culta de formación no-matemática piense que nosotros lo que hacemos es…mmm… ¿contar? ¿resolver problemas de lógica como los de los libros de pasatiempos? Y en una ausencia completa de humildad piensan que la matemática es algo completamente inútil. ¡Cómo no va a ser inútil resolver pasatiempos de manera profesional! Creo que toda conferencia divulgativa debería empezar indicando algo así:
“Señores, lo que van a ver aquí está muy alejado del campo en cuestión. Es algo divertido y fácil de entender, no como los problemas reales que tratamos de resolver.”
Vamos ahora al tema de la conferencia en cuestión: las series lógicas. Una serie lógica es una colección de símbolos o números finita y para la que se necesita continuación. Por ejemplo, 2,4,8,16… En la conferencia se nos habló de la falta de unicidad para la continuación. Es decir, que dada una serie la respuesta correcta no es única. En el ejemplo anterior todo el mundo diría que sigue el 32, pero 31 también es una respuesta correcta (se puede razonar, si alguien tiene interés que ponga su duda en los comentarios y la responderé).
Guillermo Martínez usó un argumento basado en interpolación para concluir que dada una colección finita de números hay una manera de razonar que permite continuar la serie con cualquier otro número. La idea es que dada la serie 2,4,8,16, la respuesta puede ser
Así, dada una colección aparentemente aleatoria de números, podemos construir un polinomio interpolador que nos sirva de Ley y nos “explica” como “se han obtenido”. El tema de lo que significa “aleatorio” surge aquí, pues si dada una colección siempre podemos encontrar una Ley… ¿qué significa una colección de números aleatorios? Por ejemplo, en Matlab tenemos la función rand, que nos da un número entre 0 y 1 “aleatorio”. Claramente estos números no son aleatorios, los genera un ordenador usando una fórmula. Sin embargo usando los criterios existentes (que no nos dicen cuándo una secuencia es aleatoria sino cuándo una secuencia PASA POR aleatoria) son indistinguibles de números verdaderamente aleatorios (los que se sacasen con los ojos vendados de un bombo). Por lo tanto en la práctica nos sirven.
El problema de la inferencia de una Ley dado un número finito de experimentos es irresoluble, ya lo dijo Wittgenstein, sin embargo es lo que hace la física todos los días de manera más que aceptable. Basta con tener una Ley “dinámica”, me explico, si vale la usamos, cuando no valga la cambiamos por una que nos cumpla todos los nuevos experimentos y así vamos tirando para delante. Y he de decir que de manera más que satisfactoria. Por lo tanto, quiero desde aquí tranquilizar a todos los asistentes a la conferencia a los que vi visiblemente sorprendidos, casi en estado de shock. De acuerdo, no podemos saber si la Ley que usamos es la correcta, pero, mientras nos funcione bien ¿qué más nos da? Lo demás son pasatiempos.
(Esta es una entrada par participar en el X Carnaval de Matemáticas (http://carnavaldematematicas.drupalgardens.com/) organizado por La Ciencia de la Mula Francis (o Francis (th)E mule Science’s News, http://francisthemulenews.wordpress.com/))
En esta entrada para nuestro blog (http://ambages.es/blog/) vamos a hablar de las posibles maneras de contar que se nos ocurren y sus aplicaciones a la integración.
Desde los primeros cursos en el Instituto nos hacen que aprendamos unas cuantas fórmulas para el cálculo de volúmenes y áreas de cuerpos o figuras más o menos “corrientes”, pirámides, conos, cuadrados, círculos… Más tarde, ya en Bachiller nos enseñan la genial herramienta que es la Integral de Riemann.
Este concepto es clave, por lo que vamos a gastar unas líneas recordándolo. Supongamos, por facilitar la exposición, que estamos calculando el área bajo una curva 
Observamos que esto es válido para las curvas
¿Qué os parece?, el cálculo de áreas, un problema central en la historia de la humanidad ya que está ligado a los campos de cultivo y por lo tanto al yantar, resuelto sin fórmulas complicadas ni nada parecido. Es cosa simplemente de ‘ir tapando con rectángulos’.
De esto ya se dio cuenta el genial Arquímedes (el que gritó ¡Eureka! y salió corriendo de la bañera). Así en su ‘Sobre la cuadratura de la parábola’ para calcular el área encerrada por un segmento de parábola lo que hace es tapar dicha superficie con triángulos isósceles de manera que lo que queda fuera de estos triángulos vuelven a ser segmentos de parábola similares al primero y de esta manera recurrente, sumando las áreas d elos infinitos triángulos calcular la superficie encerrada por la parábola inicial. Me gustaría señalar que la serie dada por las áreas de los triángulos es una serie geométrica de razón 1/4 y que Arquímedes la sumó entera. Es la primera vez en la historia (al menos que yo sepa) que se suma COMPLETA una serie geométrica (que es quizá la más fácil de las series), pues si bien en los Elementos de Euclides se da una fórmula para calcular la n-ésima suma parcial para cualquier n esto no es lo mismo que sumar la serie completa, hay una sutil diferencia.
Hasta ahora hemos hablado de integrales, áreas… pero nada de contar como dijimos al principio. Ahora vamos a eso. Supongamos que somos pobres becarios de investigación (lo de pobre es en sentido literal), y que queremos contar nuestro escaso peculio. Tenemos así monedas de 2 euros, de un euro, de 10 céntimos… vamos, de todas las monedas que hay. Una manera de contarlas es ponerse pacientemente, ir una a una e ir sumando. Primero cogemos una de 1 euro, luego una de 2 euros, luego una de 5 céntimos… Eso es lo que hace la integral de Riemann.
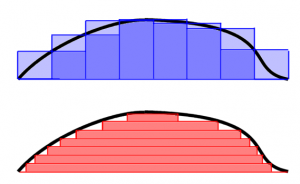
Pero esta manera de hacerlo no es la única. También podemos agrupar las monedas según su valor y contar cuantas tenemos en cada grupo. Así juntamos y nos salen 3 monedas de 2 euros por un lado, 10 monedas de 5 céntimos por otro… Ahora sólo hemos de multiplicar el número de monedas por su valor y sumar los resultados para cada grupo. Esta idea, para el cálculo integral, se llama Integral de Lebesgue. Lo que se hace es tapar con rectángulos según la altura de la función. Así en la figura adjunta (sacada de la wikipedia) se ve en azul la manera de integrar de Riemann y en rojo la manera de integrar de Lebesgue. Parece una tontería sin consecuencias, pero tiene unas consecuencias teóricas y prácticas importantisimas, de manera que es la Integral que los matemáticos usamos normalmente. Sin embargo, como es una entrada divulgativa, y no una clase de teoría de la medida lo voy a dejar aquí.
\bigg{|}_{s=0}=\frac{d}{ds}\left(\int_0^t L(y(t))dt\right)\bigg{|}_{s=0}](https://s0.wp.com/latex.php?latex=%5Cfrac%7Bd%7D%7Bds%7DA%5By%5D%28s%29%5Cbigg%7B%7C%7D_%7Bs%3D0%7D%3D%5Cfrac%7Bd%7D%7Bds%7D%5Cleft%28%5Cint_0%5Et+L%28y%28t%29%29dt%5Cright%29%5Cbigg%7B%7C%7D_%7Bs%3D0%7D&bg=T&fg=000000&s=0 "\frac{d}{ds}A[y](s)\bigg{|}_{s=0}=\frac{d}{ds}\left(\int_0^t L(y(t))dt\right)\bigg{|}_{s=0}")
