Esta es nuestra entrada para el Carnaval de Matemáticas 2.2 (alojado esta vez en Gaussianos).

Muchas veces se ha escrito sobre la relación entre los caminos aleatorios y la ecuación del calor, y quizá próximamente tratemos nosotros ese tema. Sin embargo hoy vamos a ver una aplicación poco conocida de esa relación. En esta entrada vamos a tratar brevemente una manera de emplear las matemáticas, y mas concretamente los caminos aleatorios o las trayectorias brownianas, para que un ordenador sepa qué imagen está ‘viendo’. Ahora que han puesto unos radares de tramo (que funcionan memorizando las matrículas de los coches y midiendo tiempos para calcular la velocidad media del tramo donde está el radar) en las carreteras españolas este problema tiene una clara aplicación práctica.

Desde hace unos años el tratamiento de imágenes usando ecuaciones en derivadas parciales es un área de investigación matemática floreciente. Normalmente tratan el problema de detectar los contornos de una imagen o de suavizarlos (de manera que veamos mejor la imagen). Nuestro problema es ligeramente distinto. Nosotros, dada una silueta (es decir un contorno cerrado y suave que encierra un área negra mientras que lo de fuera es blanco), tenemos que enseñar al ordenador a sacar propiedades de los contornos de manera que aprenda a distinguir entre las distintas siluetas.

La manera usual de extraer propiedades de una silueta es ‘medir’ y ‘clasificar’ los puntos del interior del contorno en función de su posición relativa a la curva que delimita la silueta (a partir de ahora la denotaremos S, mientras que el contorno será ). Esto puede hacerse por ejemplo con la distancia mínima. Es decir, a cada punto interior se le asigna un valor que viene dado por la distancia mínima a . Se forma así lo que se llama una segmentación (se divide la silueta en partes) que no es muy regular (he apostado con David a que vosotros, los lectores, podéis encontrar un ejemplo muy rápido…). Para utilizar esta manera de relacionar puntos del interior con la frontera lo que se hace es resolver la ecuación eikonal con condiciones de borde Dirichlet sobre la silueta: es decir se resuelve . Esta manera tiene ciertas desventajas, algunas matemáticamente obvias. Por ejemplo podemos convencernos rápidamente de que la ecuación anterior no tiene una única solución. En efecto, consideremos el problema en una dimensión: tenemos así a ecuación diferencial ordinaria en un intervalo acotado. Podemos construir infinitas soluciones, basta con ir construyendo triángulos con lados de pendiente 1 o -1. Podemos construirlos más grandes, más pequeños, unos pocos o muchos… Cada una de estas construcciones será una solución ‘débil’ (otro día hablaremos más de la soluciones débiles, hoy lo dejo caer sólo :P).

Así que si descartamos la aproximación anterior tenemos que proponer una nueva… para que no nos digan que hacemos críticas destructivas. Así que lo que hacemos (ver la referencia más abajo) es considerar un camino aleatorio, y más concretamente consideramos el tiempo medio, que denotamos por que tarda una partícula que siga dicho camino aleatorio en golpear si inicialmente estaba en un punto . Cuando a cada le asignamos este tenemos una segmentación. ¿Qué ecuación diferencial cumple? En (1) la motivan razonando de la siguiente manera: sea el tiempo medio que emplean estas partículas en golpear el contorno del dominio saliendo desde el punto (interno de la silueta ). Entonces si se tiene que , si no, por ser las probabilidades uniformes se tiene que se puede calcular conociendo los valores de los puntos vecinos. Efectivamente, si estamos en un punto y conocemos el valor de en los puntos inmediatamente vecinos lo que podemos hacer es ‘gastar un movimiento’ en movernos a un punto vecino (siguiendo el camino aleatorio uniforme, lo que nos da una probabilidad 1/4 de elegir un determinado punto adyacente) y sumarle el tiempo medio que se emplea desde este nuevo punto. Por lo tanto se tiene que el valor es

Entonces observamos que la discretización del Laplaciano es
y por lo tanto la ecuación anterior es una versión discretizada de

Una manera rigurosa de obtener la misma conclusión es considerar la ecuación
con datos de borde Dirichlet homogéneos. Sea ahora . Entonces se tiene

La idea de la demostración es aplicar la fórmula de It\^ o (ver (2) o (3)) al proceso $u(X_s)$, donde $X_s$ es un movimiento browniano, obteniendo la fórmula siguiente tras tomar esperanzas

Ahora usamos las condiciones de borde y la ecuación para obtener
concluyendo la demostración.

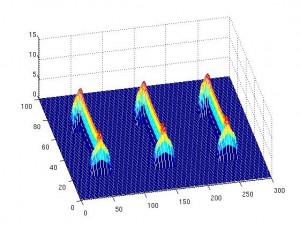
Una vez que tenemos solución de la ecuación de Poisson anterior lo que hacemos es definir nuevas funciones y y (entre otras). La función tiene ciertas propiedades que la hacen interesantes, pero para el tratamiento de imágenes lo más importante es que los valores altos de indican concavidades (allí el gradiente es grande) y que podemos utilizar el método del umbral para dividir nuestra forma en partes sin perder información. 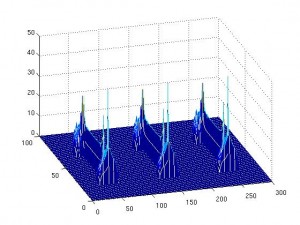La función (cuyo operador es el 1-Laplaciano) tiene la propiedad de que ciertos valores se alcanzan en zonas curvadas. Por lo tanto sirve para encontrar esquinas en nuestra forma. Los valores negativos de indican concavidades. Cuanto más negativo más ‘picuda’ es la concavidad. Al reves también funciona, los valores altos indican convexidades. Así extraemos información de la imagen y el ordenador puede discernir entre ellas.

Para el lector familiarizado con Matlab dejamos un código. Con estas funciones se puede experimentar un poquito lo que hemos estado diciendo.

function [img,img2,u,t,cnt]=imagessor(tol,itmax,image)
%this program use the sor method for solve the poisson equation in a silhouette
%tol is the tolerance
%itmax is the maximum number of iterations
%image is an png image.
%Rafael Granero Belinchon

tic
img=imread(image);
figure;imagesc(img);
input(‘Press any key’)
img=double(img);
[H,W]=size(img);
w= 2 / ( 1 + sin(pi/(H+1)) );%our overrelaxation parameter
for i=1:H
for j=1:W
img2(i,j)=abs(img(i,j)-255); %change white for black and viceversa
end
end
img2;
figure; imagesc(img2);
input(‘Press any key’)
clear i,j;
%now we start with the algorithm. Like maybe it will be difficult put the geometry of the silhouette
%we use the easy bounday conditions to treat all the image, but we only solve the poisson inside the silhouette.
%This maybe is not efficiently, but is easier.
u=img2;
v=u;
err=1;
cnt=0;
while((err>tol)&(cnt<=itmax))
for i=2:H-1
for j=2:W-1
if (img2(i,j)==0)

else
v(i,j)=u(i,j)+w*(v(i-1,j) + u(i+1,j) + v(i,j-1) + u(i,j+1) +1 – 4*u(i,j))/4;
E(i,j)=v(i,j)-u(i,j);
end
end
end
err=norm(E,inf);
cnt=cnt+1;
u=v;
end
u=flipud(u);
figure;imagesc(u);
mesh(u)
t=toc;

function [Phi,t]=phi(u,NGu)
%This program calculate the function phi=u+NGu^2
%NGu is the norm of the gradient of u
%Rafael Granero Belinchon

tic
[H,W]=size(NGu);
for i=1:H
for j=1:W
Phi(i,j)=u(i,j)+NGu(i,j)^2;
end
end
t=toc;

function [Psi,t]=psiimages(u,Gux,Guy,NGu)
%This program calculate the function psi=-div(gradient(u)/norm(gradient(u))
%NGu is the norm of the gradient of u
%Gux is the first component of the gradient,
%Guy is the second one
%Rafael Granero Belinchon

tic
[H,W]=size(NGu);
for i=2:H
for j=2:W
Psix(i,j)=((Gux(i,j)-Gux(i-1,j))*NGu(i,j)-Gux(i,j)*(NGu(i,j)-NGu(i-1,j)))/NGu(i,j)^2;
Psiy(i,j)=((Guy(i,j)-Guy(i,j-1))*NGu(i,j)-Guy(i,j)*(NGu(i,j)-NGu(i,j-1)))/NGu(i,j)^2;
Psi(i,j)=-Psix(i,j)-Psiy(i,j);
end
end
t=toc;

function [Gux,Guy,NGu,t]=gradient(u)
%This program calculate the gradient and its norm
%Gux is the first component of the gradient,
%Guy is the second one
%NGu is the norm of the gradient
%Rafael Granero Belinchon

tic
[H,W]=size(u);
for i=2:H
for j=2:W
Gux(i,j)=u(i,j)-u(i-1,j);
Guy(i,j)=u(i,j)-u(i,j-1);
NGu(i,j)=(Gux(i,j)^2+Guy(i,j)^2)^0.5;
end
end
t=toc;

(1) L.Gorelick, M.Galun, E.Sharon, R.Basri, A.Brandt, ‘Shape Representation and Classification Using the Poisson Equation’, IEEE transaction on pattern analysis and machine intelligence, 28 (2006), no.12, 1991-2004.

(2) H.Kunita, Stochastic differential equation and stochastic flows of diffeomorphism, Lecture Notes in Math. vol 1097, Springer, 1984.

(3) H.Kunita, Stochastic flows and stochastic differential equations, Cambridge studies in advanced mathematics, 1997.