El día 18 de Septiembre hizo 229 años de la muerte de Leonhard Euler (ya lo dijimos aquí), así que ¿qué mejor momento para continuar con la serie sobre el problema de Basilea? Ésta serie ya consta de dos entradas (ver aquí y aquí) contando un poco cómo se formula el problema y qué avances se han dado. Vamos a resumirlo un poquito.
El problema de Basilea es calcular la suma de la serie
Jacob Bernoulli fue capaz de probar que la serie efectivamente convergía, i.e. que la suma tiene un valor finito. Una vez que se sabe eso uno puede ir sumando términos a ver qué número va quedando. El problema es que la serie converge muy despacio y hay que sumar muchísimos términos para tener una cantidad aceptable de decimales. Y es aquí donde entra Euler al escribir una serie equivalente que converge mucho más rápido, de manera que hay que sumar menos términos para obtener los mismos decimales.
Veamos qué hizo Euler llegados a este punto. Tenemos que recordar que si tenemos un polinomio
cuyas raíces (reales) son
Con esto en mente observamos que
Así Euler escribe, usando la serie de Taylor,
de donde, si dividimos por x y suponemos que podemos usar la propiedad anterior de los polinomios para una serie de potencias, obtenemos
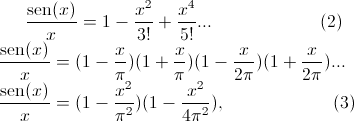
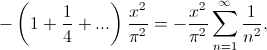
y ahora, igualando con (2), obtenemos el resultado
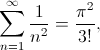
Éste resultado es correcto, pero tiene un enorme “pero”: el argumento es erróneo. No se puede hacer ese desarrollo como producto de las raíces para series. Por ejemplo podemos considerar
que, por tener las mismas raíces que el seno, ¡debería tener el mismo producto infinito! Esta prueba fue muy criticada por la comunidad y Euler siguió trabajando en desarrollos de productos infinitos para el seno de manera que pudiese acallar las quejas con una demostración completamente rigurosa y no sólo con un escueto “pues mi aproximación y el valor exacto que he calculado son iguales…”, pero eso lo dejaremos para otro día…
–Referencias:
Rafael Granero Belinchón, El problema de Basilea: Historia y algunas demostraciones. La Gaceta de la RSME, vol 12, num 4, pag 721-737, 2009.
E. Sandifer, Basel Problem with Integrals, MAA Online, 2004, disponible aquí.
Y aquí un conversor entre fórmulas de Latex e imágenes.
–Nota: Con esta entrada participamos en el Carnaval de Matemáticas en su edición 26, organizado esta vez por ZTFNews.
