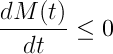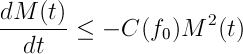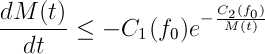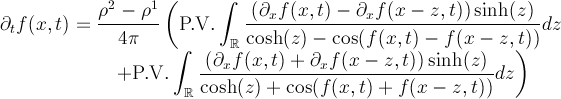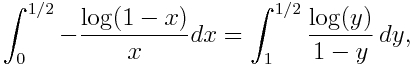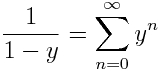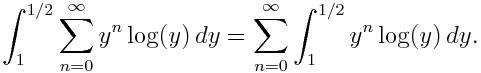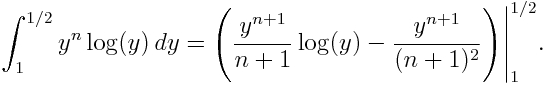Desde el año 1857 en el que Riemann usó la palabra ‘móduli’ como sinónimo de parámetro, los matemáticos la siguieron aplicando (de manera un tanto imprecisa) para designar aquellos parámetros que miden o describen la variación de objetos geométricos en Geometría Algebraica. Sin embargo, no fue hasta 1960 cuando David Mumford dio una definición formal y precisa de espacios de móduli y explicó cómo construirlos obteniendo soluciones en algunos casos.
¿Por qué nos interesan los espacios de móduli?
Aunque a algunas personas les gusta ver a los espacios de móduli como objetos geométricos cuyos puntos tienen significado, quizás una forma más intuitiva de concebirlos sea como un mapa o un dibujo de un cierto conjunto. Por ejemplo, si tenemos una lista de las 17 comunidades autónomas, sus tamaños y otra lista detallando qué estados son limítrofes, será difícil bosquejar cómo es nuestro país. Sin embargo, un mapa nos permitirá hacernos una idea realista del territorio. Por tanto, en este caso, un mapa de España sería el espacio de móduli de las autonomías.
Ingredientes para la construcción de un espacio de móduli
Los espacios de móduli surgen de manera natural en los problemas de clasificación geométricos como sus soluciones geométricas. Un ejemplo típico (y real) de tales problemas es la clasificación de las curvas proyectivas complejas no singulares salvo isomorfismo (o equivalentemente, superficies de Riemann compactas salvo biholomorfismo).
Un ‘espacio de móduli’ es una variedad compleja (o variedad algebraica) cuyos puntos corresponden (de manera natural) a las clases de equivalencia de los objetos que queremos clasificar. Por tanto, si queremos construir un espacio de móduli precisaremos de los siguientes ingredientes:
- Objetos: ¿Qué objetos geométricos nos gustaría describir o parametrizar?
- Equivalencias ¿Cuándo podemos decir que dos objetos son el mismo?
- Familias: ¿Cómo permitimos a nuestros objetos variar o modular?
Cabe observar que para identificar dos objetos en Matemáticas debemos usar relaciones de equivalencia y definir así un cociente, operación no inmediata en Geometría Algebraica pues algunas sutilezas deben tenerse en cuenta. Si estamos trabajando con objetos que poseen ciertas propiedades queremos que el cociente disfrute de las mismas. Sin embargo, esto no suele ocurrir pues es habitual que en el cociente no se puedan separar puntos mediante entornos abiertos (no sea Haussdorff).
Para solucionar estos problemas David Mumford desarrolló la Teoría Geométrica de Invariantes (GIT en sus siglas en Inglés) que resolvía estas cuestiones y que le valió la Medalla Fields en 1974. Su idea fue eliminar aquellos objetos ‘malos’ que nos daban problemas y construir así un objeto geométrico razonable que será el espacio de móduli. Por ejemplo, el espacio de móduli de las curvas proyectivas complejas no singulares existe pero si queremos incluir las singulares (quizás sea interesante comprender cómo las curvas no singulares pueden degenerar a aquellas singulares) debemos dejarlas fuera (las llamaremos órbitas inestables) y obtener así una variedad algebraica y, por tanto, un espacio de móduli.
Un ejemplo, por favor
Supongamos que queremos describir la colección de todas las rectas en el plano $latex\mathbb{R}^{2}$ que pasan por el origen (en adelante, por brevedad, rectas). Para empezar, una buena idea es encontrar un número que parametrice los objetos que queremos clasificar. En nuestro caso, si utilizamos coordenadas cartesianas, utilizaremos como parámetro el ángulo $\theta$ que forma la recta con el eje  en sentido antihorario y no es difícil convencerse de que
en sentido antihorario y no es difícil convencerse de que  . Por tanto, como \textbf{conjunto} tenemos una solución completa de nuestro problema de clasificación ya que a cada una de las rectas del plano le corresponde un número del intervalo
. Por tanto, como \textbf{conjunto} tenemos una solución completa de nuestro problema de clasificación ya que a cada una de las rectas del plano le corresponde un número del intervalo  .
.
Sin embargo, no podemos olvidar que estamos buscando una solución \textbf{geométrica} a nuestro problema de clasificación. Para ello, si dos rectas están cerca, sus ángulos deberán ser casi iguales y, por tanto, los puntos correspondientes en el intervalo deberían estar muy próximos. En particular, aquellas rectas  cuyo ángulo está cercano a $latex\pi$ son casi horizontales y son muy parecidas a aquellas rectas cuyo ángulo con respecto al eje
cuyo ángulo está cercano a $latex\pi$ son casi horizontales y son muy parecidas a aquellas rectas cuyo ángulo con respecto al eje  es casi cero. Por tanto, si queremos encontrar una solución geométrica a nuestro problema, debemos encontrar alguna forma de pegar el intervalo
es casi cero. Por tanto, si queremos encontrar una solución geométrica a nuestro problema, debemos encontrar alguna forma de pegar el intervalo  para que
para que 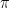 esté cerca de 0.
esté cerca de 0.
Una forma de hacer esto es tomar el intervalo cerrado ![[0,\pi] [0,\pi]](https://s0.wp.com/latex.php?latex=%5B0%2C%5Cpi%5D&bg=T&fg=000000&s=0) en vez de
en vez de  y entonces identificar los puntos 0 y
y entonces identificar los puntos 0 y 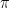 . Esta operación de pegado se hace en Matemáticas mediante una relación de equivalencia. Luego, si
. Esta operación de pegado se hace en Matemáticas mediante una relación de equivalencia. Luego, si 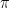 y 0 se pueden ver como el mismo punto, entonces los números cercanos a
y 0 se pueden ver como el mismo punto, entonces los números cercanos a 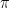 estarán próximos a los cercanos a 0. De esta forma obtenemos un círculo que es la solución geométrica de nuestro problema.
estarán próximos a los cercanos a 0. De esta forma obtenemos un círculo que es la solución geométrica de nuestro problema.
Interacción con la Física
El procedimiento descrito más arriba de estudiar los invariantes o la Geometría no del espacio original sino de un espacio de móduli construido a partir de él se interpretó más tarde como un tipo de Teoría Cuántica de Campos traduciéndose en una interacción fructífera entre la Física y la Geometría. Por ejemplo, la interacción con la Teoría de Cuerdas en Física ha sido especialmente productiva para la Geometría Algebraica pues esta teoría requiere geometrías complicadas de dimensiones altas y, de hecho, precisan de aquellos espacios (variedades de Calabi-Yau) que no se han podido tratar por medio de los invariantes clásicos.
Bibliografía:
BEN-ZVI, D.D., Moduli Spaces, Princeton Companion to Mathematics, 2008.
GARCÍA-PRADA, O. Moduli Spaces and Geometric Structures. Apéndice en Differential Analysis on Complex Manifolds, 1972.
KIRWAN, F. Moduli Saces in Algebraic Geometry. Moduli Spaces in Mathematics and Physics, Hindawi, 1998.
Fdo: David Fernández
–Nota: Esta entrada participa en el Carnaval de Matemáticas en su edición 3.1 organizado esta vez en este blog.
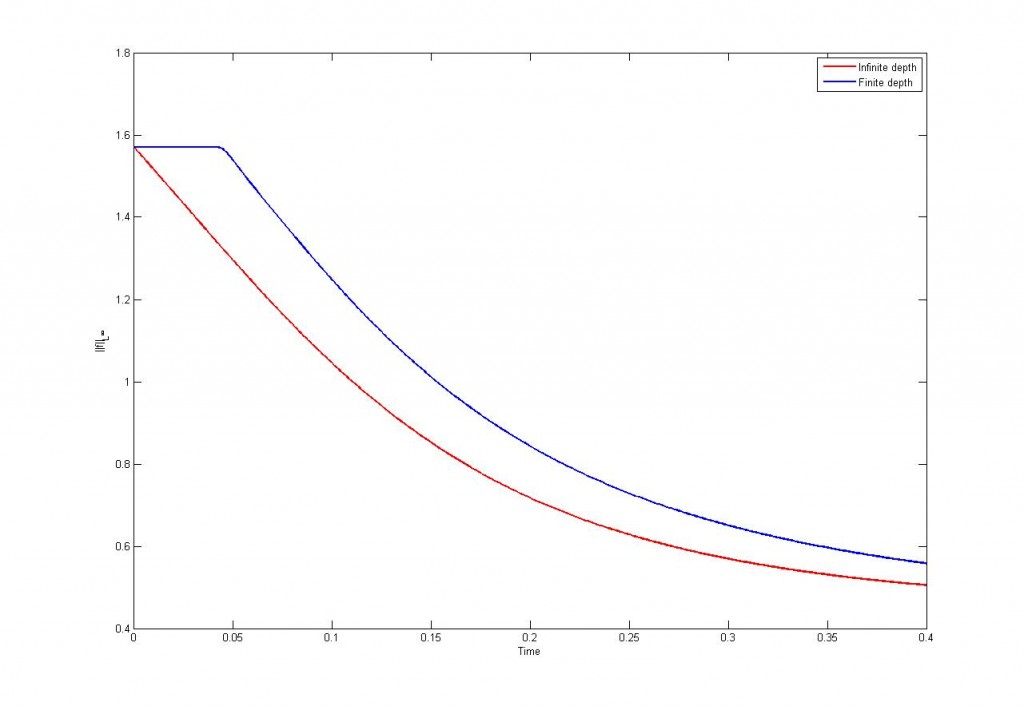
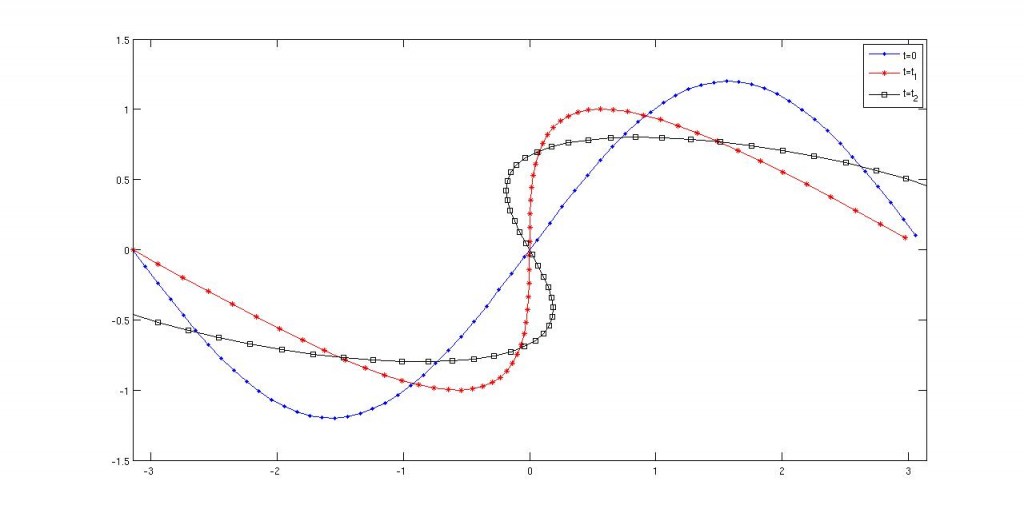
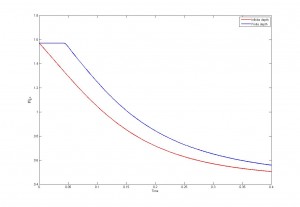
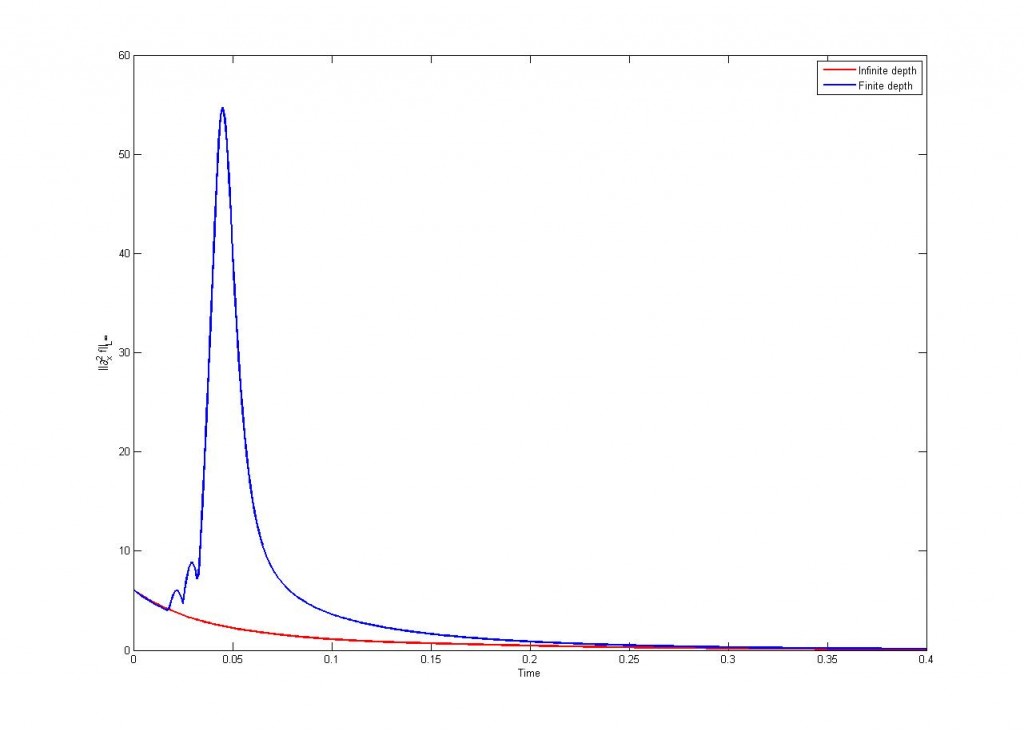
es la ola inicial. En el caso de un medio acotado la amplitud evoluciona según
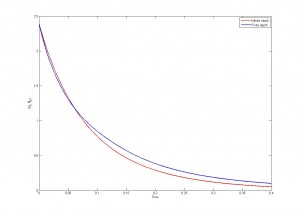
? Esta cantidad nos da una idea de cómo es la longitud de onda. Sabemos que en el caso donde el medio no está acotado se tiene que
entonces
) que involucra no sólo a
si no también a
:
entonces
y por lo tanto la ola no puede romper.