En una entrada anterior (ver aquí) os contamos cómo Jacob Bernoulli encaró el problema de Basilea, esto es, la suma de la serie
Estamos en 1730 o 1731 y es ahora cuando hace su aparición Leonhard Euler, con su artículo De summatione innumerabilium progressionum, publicado en 1738, donde utiliza un método nuevo para aproximar esta serie. Euler parte de la serie de potencias de
La divide por e integra entre 0 y 1/2, obteniendo
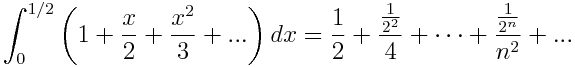
En el lado izquierdo de esta expresión hace la sustitución consiguiendo
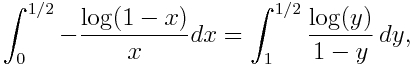 y reparando en que
y reparando en que
se obtiene
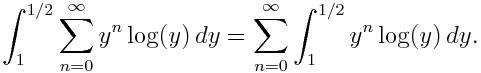
Cada uno de los sumandos se puede integrar por partes,
Agrupando de nuevo, se consigue
Podemos ahora sustituir la serie de potencias
con lo cual queda
Ahora, Euler desprecia el producto y procede igualando la expresión de la derecha con el valor que se ha conseguido de la integral de la izquierda mediante el proceso anterior. De este modo llega a
Con estos manejos poco rigurosos, Euler solucionó el problema de la baja velocidad de convergencia de la serie: gracias a las potencias de dos en el numerador, los términos de la nueva serie que ha obtenido decaen mucho más rápido, y en consecuencia la convergencia de la serie es mucho mejor. Además, Euler conocía el valor de con una gran cantidad de cifras decimales, consiguiendo así una aproximación 1.644934 que es correcta en las seis cifras decimales con la suma de sólo catorce términos de la nueva serie.
–Nota 1: Esta entrada participa en el Carnaval de Matemáticas del mes de Marzo. Ésta vez ha sido organizado por Hablando de Ciencia
–Nota 2: Para las imágenes con las fórmulas hemos usado el editor presente en esta web.
–Nota 3: El texto anterior está basado en el artículo
Rafael Granero Belinchón, El problema de Basilea: Historia y algunas demostraciones. La Gaceta de la RSME, vol 12, num 4, pag 721-737, 2009.

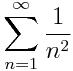
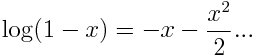
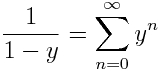
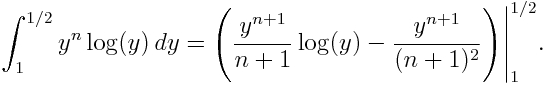
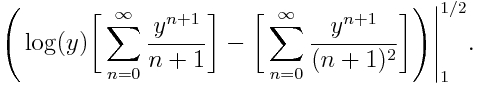
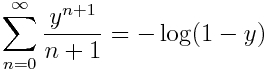
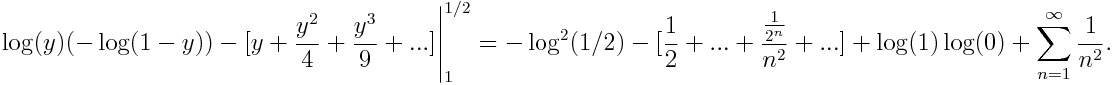
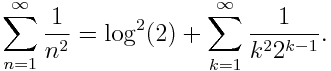
Pingback: Carnaval de Matemáticas 3.14: Hablando de Ciencia en su propio idioma | Hablando de Ciencia