Tradicionalmente los matemáticos que trabajamos en el área de ecuaciones en derivadas parciales estudiamos problemas que vienen de procesos físicos. Es el caso de la ecuación del calor, la ecuación de Poisson o la ecuación de ondas. En esta entrada vamos a exponer dos métodos para resolver la ecuación de ondas. Estos métodos al tener un planteamiento distinto dan una información distinta. Veremos así diferencias entre pensar en las ecuaciones sólo o pensar en el fenómeno que modelizan. La ecuacion de ondas es

junto a dos valores iniciales (tiene dos derivadas en tiempo) y las condiciones de contorno, que aquí tomamos dirichlet homogéneas. Esta ecuación refleja la separación del equilibrio de la cuerda en tiempo t y en el punto x.

Jean Le Rond D’Alembert demostró que si consideramos toda la recta (es decir, sin contornos) entonces podemos escribir la solución como una superposición de ondas, una que viaja hacia la derecha y otra que viaja hacia la izquierda. Estas ondas se escriben en función de los valores iniciales. Podemos hacer lo mismo en dominios acotados o semi acotados, pero es más lío.

Esta aproximación es puramente teórica, muchas ecuaciones admiten solución en forma de onda viajera (por ejemplo la de Fisher-Kolmogorov, 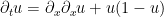). En este caso podemos esperarlo si observamos que podemos ‘factorizar’ el operador como dos operadores de transporte  

Al olvidarse del origen del problema D’Alembert encontró un método general de resolución para ciertas ecuaciones.

Veamos como lo hizo Daniel Bernoulli. Este utilizó la idea que más tarde harían famoso a Fourier, y ‘separó variables’ (no hizo exactamente lo mismo, pero el método es parecido). Así se llega a escribir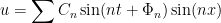

y esto tiene un explicación física clara: toda onda es una superposición de un tono fundamental y distintos armónicos, cada uno con frecuencia múltiplo de la fundamental. Así enlazamos con la acústica.

Última nota, he dicho que la solución de D’Alembert es teórica mientras que la de Bernoulli no lo es. Eso es mentira. La de Bernoulli tiene un significado importante, y es que abre las puertas a espacios de Hilbert de dimensión infinita. Lo que quiero decir al hablar de que una es teórica y la otra no es acerca de los métodos de razonamiento, D’Alembert se olvidó de cuerdas y notas musicales, viendo sólo las derivadas, mientras que Bernoulli razonó conservando la idea del fenómeno físico.

Creemos que este ejemplo indica la importancia de desarrollar de manera paralela ambos enfoques, al menos cuando la ecuación diferencial viene de un fenómeno físico del que se tiene una clara intuición.

–Nota: Con esta entrada participamos en el Carnaval de Matemáticas 2.10 , que este mes organiza Resistencia Numantina.