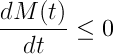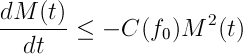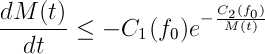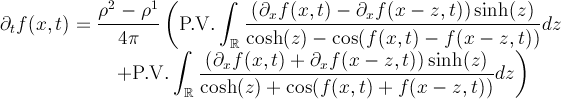Hoy vamos a hablar, procurando no ser muy rigurosos (aparecen algunas fórmulas pero se pueden saltar), de por qué la mecánica cuántica es necesaria y del principio de incertidumbre de Heisenberg. La entrada la hemos escrito de manera conjunta Rafa y yo mismo.

Werner Heisenberg, uno de los padres de la Mecánica Cuántica
Principios de incertidumbre hay muchos, básicamente no es mas que una desigualdad de cierto tipo, donde un término controla a otro. En el caso concreto que nos atañe afirma que es imposible conocer con precisión la posición y la velocidad de una partícula cuántica (para fijar ideas un electrón). Los físicos (experimentales al menos) razonan diciendo que eso es porque para detectar un electrón hay que golpearlo con un fotón y entonces cambias su velocidad.
Esto nos deja con la duda: ¿habrá algún método que permita conocer las dos cosas?
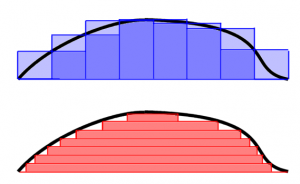
La respuesta es que no. Y el motivo, enraizado en las matemáticas, tiene que ver con la transformada de Fourier. El ‘teorema’ aquí es que si tienes una función “grande” su transformada de Fourier es “pequeña” y viceversa (se puede intuir usando la desigualdad de Haussdorf-Young por ejemplo.). ¿Cómo afecta esto a nuestro electrón?. Los impacientes estarán pensando que se me está yendo la olla.
Pero comencemos aclarando por qué todas estas cosas tan raras de la cuántica son necesarias: supongamos que tenemos un átomo de hidrógeno (un electrón y un protón), y que tanto nuestro electrón como el núcleo del átomo se comportan como partículas clásicas. Entonces, al tener el núcleo carga eléctrica positiva y nuestro electrón carga eléctrica negativa deberían atraerse por la fuerza coulombiana entre ellos. Cuando un cuerpo con carga se acelera emite radiación electromagnética (véase la
fórmula de Larmor [aquí
inglés]) perdiendo así energía.
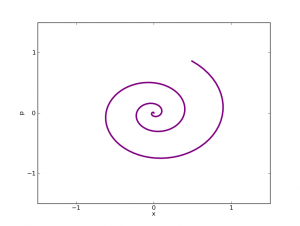
En una dimensión, la posición del electrón, x, oscilaría y caería hacia el origen de coordenadas. Su velocidad, p, también oscilaría y lo llevaría hacia el centro, radiando energía en el proceso.
Según este modelo el electrón se vería atraído irremisiblemente hacia el núcleo y acabaría chocando con éste. Pero esto implicaría ¡que no habría electrones!. En jerga científica diríamos que la materia no sería estable. Puesto que nosotros somos materia y estamos aquí las hipótesis de nuestro modelo no pueden ser correctas.
En otra entrada explicaremos la descripción de los estados en mecánica clásica y cuántica, pero permitidnos ahora que hagamos algunos supuestos. En la mecánica clásica la evolución de un sistema se describe como la trayectoria de un punto en el
estado de fases. Sin embargo, en la mecánica cuántica esto no es posible, dado que el estado de un sistema solo puede venir dado como una “probabilidad”, de modo que no existe trayectoria de un solo punto que se adecue a la evolución temporal de un estado. Aquí, pues, la incógnita será una función (con argumentos en el espacio-tiempo y con valores en los complejos)
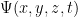
cuyo módulo al cuadrado (que es un número real) nos dará la densidad de probabilidad de que un sistema se encuentre en un cierto estado.
Esta función, que llamaremos “función de onda”, evoluciona de acuerdo con la ecuación de Schrödinger. Esta es una ecuación en derivadas parciales (EDP) “cualitativamente” hiperbólica (ver la
entrada anterior ). Para mayor simplicidad vamos a suponer aquí que no depende del tiempo, con lo que ahora nuestra ecuación de Schrödinger es elíptica y se puede escribir como la función que minimiza un funcional de acción (ya hablamos
antes de este concepto)
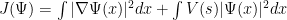
Si utilizamos, como representación de la función de onda, la base de POSICIONES, la densidad de probabilidad asociada a nuestra función de onda,

, nos dará la probabilidad de que el sistema (en este caso, nuestro electrón) esté en una zona A del espacio.
Si nos interesa el MOMENTO (i.e. la velocidad), su función de onda es la transformada de Fourier de la función de onda de posiciones,

, y esta es la madre del cordero.
En la mecánica clásica la posición y el momento eran independientes. Por eso, podríamos realizar medidas sobre una y otra cantidad sin afectar a la otra.
Ahora, no obstante, tenemos una ligadura: hay una relación que conecta la posición y el momento, y ha de cumplirse. Podemos, pues, escribir nuestro funcional en términos de las dos funciones de onda
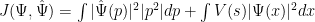
.
La formulación del principio de incertidumbre de Heisenberg es, pues,

donde C es cierta constante que podemos escribir explícitamente pero que hacerlo nos da una pereza superlativa por lo que lo dejamos ‘para el lector interesado’ ;). La constante es una ensalada de constante de Planck

,
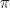
, algún dos… Puede escribirse también involucrando sólo una función de onda de la misma manera que se hace con el funcional.
Hemos dicho que

nos da una probabilidad, con función de densidad
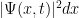
. Así observamos que en realidad el término
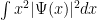
es la
varianza de nuestra variable aleatoria

(que asumimos tiene media x=0, es decir, que nuestro electrón está más o menos rondando el origen de coordenadas espaciales).
Entonces si entendemos esas ‘normas’ de los gradientes como los “errores” (utilizaremos esta palabra aquí a modo explicativo, pero hay que ser cautos con la terminología), veremos que un error pequeño en alguna de nuestras mediciones, para fijar ideas, la posición, implica que el error del momento (es decir, de la velocidad) tiene que ser alto para que el producto sea mayor que una constante. Es más: cuanto mejor midamos una (menor error) mayor es el error de la otra. ¡Qué vida más dura la nuestra!
No he hablado nada claro en este último párrafo, y los exigentes se habrán quedado pensando que me explico muy mal (quizá tengan razón). Hemos calculado un par de ejemplos ilustrativos usando python. Hemos supuesto que es unidimensional y que nuestras funciones de onda toman valores en los reales y no en los complejos. No lo hacen, pero sed generosos con nosotros que esto es sólo una afición.
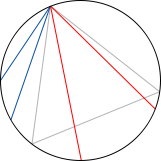
Supongamos que nuestra onda es como la de esta figura
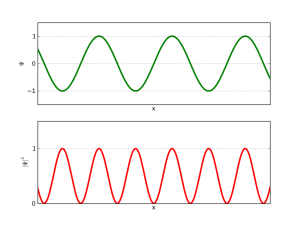
Si la funcion de onda es como un seno, la longitud de onda (o el momento) está bien definida.
Entonces por la
fórmula de De Broglie, que conecta la visión de partículas con la de ondas, tenemos una velocidad definida (con poco o ningún error), que depende de la longitud de onda (¡otra entrada por hacer!). Esto de nuevo enlaza con nuestra transformada de Fourier, dado que este tipo de transformadas nos llevan desde el espacio de posiciones al espacio de momentos. Sin embargo, no conocemos nada de la posición, pues la probabilidad no se decanta por ninguna zona en particular y salvo puntos donde nunca estarán los electrones por lo demás no podemos decir nada. (Para el lector interesado, decir que esta función de onda no está bien definida en el espacio de posiciones: no es normalizable)
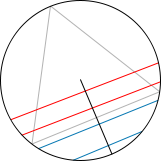
Otro caso interesante es algo así como:
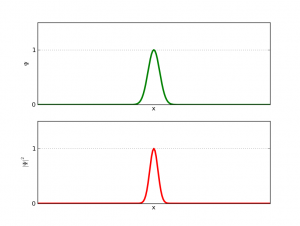
Un paquete gaussiano es una elección "popular" de función de onda porque tiene incertidumbre mínima
En esta segunda imagen tenemos una función tal que al hacer el cuadrado obtenemos una zona que acapara casi toda la probabilidad, un entorno del origen (como la vida misma, unos pocos acaparan casi toda la proba…, digo, billetes). Es decir, casi sin error podemos saber su posición; sin embargo, no podemos usar la fórmula de De Broglie para calcular su velocidad, pues ¿quién me dice su longitud de onda?…
Para ir concluyendo ¿cómo enlaza esto con los gradientes (es decir, las derivadas)?, observamos que una función como la de la figura 1 tiene un gradiente ‘pequeño’, mientras que una función cómo la de la figura 2 tiene un gradiente ‘grande’. Sólo hay que ver que ese pico tiene una derivada bien grande. Así tenemos que entender que los gradientes me dan una idea del error, pero cambiando la variable. Es decir, una gradiente alto en las x me dice un error grande en las p y un error pequeño en las x. Aunque no hemos hablado de ello, esto tiene que ver con la estructura geométrica de las
ecuaciones del movimiento Hamiltonianas (ya llegará, ya llegará…).
Es sorprendente (pero usual) cómo la física a veces acaba teniendo que ver con ideas abstractas de las matemáticas (al revés también ocurre).
Hay más que contar, pero se está insinuando una entrada muy larga, así que en la segunda parte de esta entrada escribiremos más acerca de los desarrollos matemáticos de la Transformada de Fourier y de si se puede obtener alguna propiedad física desde las matemáticas.
=======================