Cualquier estudiante de física tiene claro o al menos intuye cómo aparecen las matemáticas al estudiar problemas de física. Hoy vamos a hablar de cómo aparece la física en un teorema abstracto de matemáticas.

Hay desigualdades que son muy importantes y útiles. De la que voy a hablar ahora también tiene esta característica, aunque aquí la llamaré desigualdad de Poincaré.

Sea 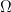un dominio regular, o dicho sin palabras de brujo, un subconjunto del espacio cuya frontera es suave, por ejemplo, un círculo. El teorema afirma que para toda función de 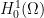existe una constante tal que se tiene

Para que no se nos empiece a calentar la cabeza vamos a decir que nuestras ues son derivables y se anulan en el borde del dominio 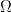y nos vamos a olvidar de las H. Con la notación 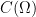reflejamos que la constante depende del dominio.

Esto, a priori, es un teorema abstracto de existencia de una constante. Como la demostración no es constructiva no tenemos ni idea de que constante es.

Nos vamos a cambiar de tercio y vamos a considerar el problema de la guitarra. Es decir, tenemos una cuerda fija en sus extremos, y queremos saber que longitudes de onda (sonidos al fin y al cabo) nos aparecerán. En el caso de una cuerda cuya amplitud de oscilación sea pequeña y su rigidez despreciable (entonces decimos que el sistema es perfectamente lineal), las frecuencias de vibración serán proporcionales al inverso de la longitud de onda de cada modo de vibración y por tanto múltiplos enteros de la frecuencia fundamental, que es la correspondiente al modo de mayor longitud de onda. Matemáticamente se trata de un problema de ecuaciones diferenciales.

Nuestro problema, despues de muchas simplificaciones, se convierte en

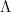y condiciones de borde cero , donde L es la longitud de la cuerda. Sabemos que hay un conjunto de constantes posibles, y ninguna más. Además sabemos que tienden a infinito y que la primera es la más pequeña. En concreto para dominios fáciles (hay que cambiar las condiciones de borde adecuadamente) tenemos hasta fórmulas. Por ejemplo, para un círculo se tiene que el primer (y más pequeño) autovalor (así se llaman los 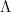) 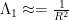, donde R es el radio del círculo. En el caso de cuadrados es fácil también. Se tiene donde L es el lado del cuadrado. Con esto hemos concluído con los tambores sencillos, vamos con las cuerdas. En este último caso se tiene .

¿Cómo enlaza esto con nuestra constante C anterior?. Fácil, multiplicamos por u e integramos por partes la ecuación (2). De esta manera casi obtenemos (1), lo que ocurre es que la constante esta en el lado equivocado y tenemos igualdad. Pasar la constante dividiendo y ver que si la constante 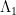era la más pequeña su inverso es el más grande no nos lleva ni 2 segundos. Resumiendo, para ciertos dominios fáciles tenemos una expresión para la constante, que además tiene que ver con el ruído que hacen los tambores o las cuerdas de guitarra. Y es que esta constante no es un número puro, sino que tiene dimensiones de espacio a la menos 2 (aunque esto no es difícil de ver a partir de las fórmulas o la propia ecuación (2), no es tan importante).

Espero que encontreis esto tan interesante como yo. Y es que las relaciones entre las matemáticas y la física aparecen cuando uno menos se lo espera y sin pedir permiso.

PD: Esta entrada es nuestra participación en el Carnaval de Fïsica de Enero que organiza el blog El tao de la Física.