Autores: David Szwer y Hannes Busche,
Joint Quantum Centre (JQC) Durham-Newcastle, Department of Physics,
Durham University, UK.

Traducción de David Paredes

(Este artículo apareció originalmente en el blog 2Physics, y trata sobre el artículo a Maxwell et al. Phys. Rev. Lett., 110, 103001 (2013). Abstract. [versión libre en el arXiv])

Resumen:
El Procesado y la Comunicación cuánticas necesitan portadores robustos de información cuántica (qubits) y los fotones en frecuencias ópticas son candidatos idóneos: la luz se puede transmitir fácilmente utilizando tecnologías como las fibras ópticas, y casi no interactúa con otros fotones o el ambiente. Sin embargo, para procesar la información que portan se necesitan interacciones controlables entre los fotones que transportan esa información. Físicos en la universidad de Durham en el Reino Unido han combinado dos técnicas avanzadas de óptica cuántica con un sintetizador de microondas para controlar las interacciones entre fotones individuales [1,2]. Los fotones son almacenados en una nube de átomos de rubidio en forma de “polaritones Rydberg”. Gracias a que las interacciones entre ellos son de largo alcance, solamente un fotón puede ser almacenado en un volumen de unos cuantos micrones cúbicos, limitando el número total de fotones almacenados a unos tres. Las microondas manipulan los fotones mientras que están almacenados, forzándolos a interactuar en maneras cuyos detalles aún no se comprenden completamente. La habilidad para inducir interacciones al nivel de fotones únicos, y de controlarlas utilizando microondas, podría ofrecernos un nuevo punto de vista en el desarrollo de futuras tecnologías cuánticas.

Un haz de luz es una de las cosas con menos sustancia que se puede encontrar. Es la esencia misma de algo rápido e inaferrable – tanto, que hasta Einstein inventó la relatividad específicamente porque no podía imaginarse cómo sería la luz si estuviese parada. Y aunque la luz es reflejada por espejos y se dispersa debido a otros objetos, nunca consideramos que dos haces de luz puedan “rebotar” entre sí.

Sin embargo, en ciertos experimentos los físicos no solamente pueden “parar” la luz, sino hacer que la luz interactúe con la luz misma. Nuestro trabajo consigue ambos efectos: hacer que la interacción funcione al nivel de pocos fotones, y controlarla con microondas. El “truco” que nos permite hacer estas cosas es que la luz no tiene por que ser siempre la onda electromagnética pura que es en el vacío. Cuando la luz atraviesa un material, como el vidrio o el agua, el campo eléctrico de la luz distorsiona ligeramente a los átomos que componen el medio, y estos, por su parte, afectan a la luz. Esto hace que la luz reduzca su velocidad (hasta la mitad de la velocidad de la luz en el vacío, o menos), que es el efecto responsable del funcionamiento de las lentes, las fibras ópticas, los arcoiris y otros fenómenos. La materia responde a la luz casi siempre de manera lineal, de tal modo que la distorsión producida por haz de luz no afecta a otro. Cuando la intensidad es muy grande, pueden aparecer fenómenos no lineales que permiten que la luz interactúe con la luz.  Sin embargo, estos efectos solo se manifiestan a muy altas intensidades (usualmente). Además, a nosotros nos interesan las propiedades cuánticas de la luz que solo se manifiestan al nivel de pocos fotones, o uno solo. Cada fotón tiene una cantidad minúscula de energía: un puntero laser rojo normal (que emita 1mW de potencia) produce 3 mil billones de fotones ( un 3 seguido de quince ceros) por segundo, pero ninguno de ellos interactúa con ningún otro. Los fotones casi nunca interactúan, no “se enteran” de que los otros están alrededor.

Para ralentizar los fotones, pararlos completamente y hacerlos interactuar, necesitamos diseñar el medio en el que se mueven. Comenzamos con una nube muy fría y muy ligera de átomos de rubidio (que, usualmente, es un metal sólido) creado utilizando técnicas láser de enfriamiento y captura [3]. El gas, en este estado, está un millón de veces más diluido que el aire normal (contado como el número de átomos por unidad de volumen), de modo que el experimento se tiene que llevar a cabo en una cámara de vacío. Además, este gas necesita estar MUY frío, solo 10 μK (una diezmilésima parte de grado sobre el cero absoluto), porque si los átomos se mueven demasiado deprisa pueden distorsionar la luz que están atrapando.

Figura 1: Niveles de energía relevantes, mostrando las lineas espectrales de la señal a 780 nm (rojo) y el haz de control a 480 nm (azul). y las microondas que conectan dos niveles Rydberg.

Gases como el rubidio son útiles porque tienen lineas de resonancia muy fuertes – frecuencias de luz específicas interactúan muy fuertemente con el material y corresponden a transiciones entre los niveles de energía discretos del átomo. Nosotros utilizamos dos lineas en el rubidio, que tienen longitud de onda 780nm (menos de una milésima parte de un milimetro, de color rojo tenue)  y 480 nm (azul brillante). La luz roja es la señal que almacenamos. Esta señal excita átomos normales, del estado energético más bajo (llamado fundamental) a un nivel excitado concreto. Después, la luz azul afecta a esos átomos excitados, y los promueve a niveles aún más altos, llamados estados “Rydberg”. Esto afecta a la respuesta de los átomos a la luz roja, no solamente evitando que la luz se disperse, sino también ralentizándola muchísimo al mezclarla con la distorsión atómica. Si apagamos la luz azul mientras que la señal está viajando por la nube, detenemos los fotones rojos y son transformados totalmente en una distorsión atómica. A este patrón específico de excitaciones Rydberg se denomína Polaritón (véanse estas dos entradas anteriores)

A diferencia de los fotones, los estados Rydberg interactúan entre ellos en modo extremadamente fuerte, causando cambios en las frecuencias de resonancia necesarias para excitar otros átomos cercanos a estados Rydberg. Dado que una excitación al estado Rydberg deja al resto de átomos cercanos fuera de la resonancia con el laser azul, un efecto de “bloqueo” tiene lugar, previniendo que se excite más de un átomo a una distancia de unos micrones. Si los fotones están mezclados con los estados Rydberg, como en nuestra nube, los fotones obtienen (de manera efectiva) la habilidad de interactuar fuertemente, y el bloqueo también se aplica a ellos, imponiendo una separación mínima entre fotones. Si las particulas de luz están muy juntas, son dispersadas hacia afuera de la nube debido al bloqueo. Si la nube es lo suficientemente densa, esto hace que un haz laser continuo sea filtrado para dar lugar a una serie de fotones individuales, como ha sido demostrado recientemente por un grupo en el MIT [4]. Por otra parte, también podemos parar la luz dentro del medio y permitir que el bloqueo funcione mientras que los fotones están siendo almacenados – este efecto no solo ha sido explotado en nuestro grupo, sino también por un grupo en Georgia Tech donde una fuente de fotones individuales ha sido implementada [5]. Una fuente de fotones individuales que funcione de manera correcta y segura es importante para otros experimentos cuánticos, así como para la llamada “criptografía cuántica” [6].

Nuestra nube es lo suficientemente grande como para que 3 polaritones quepan en linea, y cada uno de ellos contiene un fotón compartido entre un montón de átomos. Debido al efecto de bloqueo, estos están separados por una distancia llamada “radio de bloqueo”, que mide la fuerza de las interacciones entre átomos Rydberg. Esta interacción es comunmente llamada “interacción de van der Waals“, y es la misma fuerza que mantiene a las moléculas unidas en la mayoría de materiales solidos que nos rodean.

Una vez que tenemos fotones almacenados, el siguiente paso es hacer pasar microondas por la nube que sean resonantes con una transición particular entre dos estados Rydberg. Uno de estos estados es el que hemos utilizado para almacenar los fotones (que llamaremos “S”) y el otro estaba previamente vacío (al que llamamos “P”). La luz azul que utilizamos para el almacenamiento es tal que solamente interactua con el estado S y no el P, de modo que solamente recuperamos el fotón si el polaritón se encuentra en S. Si tuviésemos solamente un polaritón en S, esta transición daría lugar a las llamadas oscilaciones de Rabi entre el estado S y P, de modo que si encendemos las microondas durante una cantidad de tiempo adecuada, la excitación se habrá transferido al estado P y al intentar recuperar el fotón con el haz laser azul no podríamos.

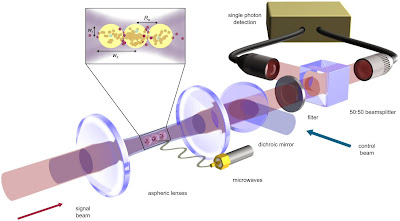
Figura 2: Diagrama del experimento que muestra la nube de átomos con 3 polaritones almacenados. Los dos detectores de fotones únicos aquí mostrados se utilizan para probar que el número de fotones recuperados es limitado, haciendo uso de un interferómetro de Hanbury Brown y Twiss [7.8].

En vez de un único polariton, nos podemos preguntar: ¿qué ocurre cuando los polaritones no están aislados, sino que tienen “vecinos” con los que interactuar? Las microondas los hacen oscilar a la misma velocidad… Para empezar, los fotones solo se recuperan cuando todos los polaritones vuelven a S. Esto da lugar a las oscilaciones (que vemos en la Figura 3)  que tienen los “valles” más amplios y las “crestas” más puntiagudas, y la forma concreta que tienen nos ayuda a estimar el número de polaritones que tenemos en el medio. Además, mientras que los polaritones están entre medias de S y P, adquieren unos momentos dipolares enormes (el equivalente electrostático de una barra imantada minúscula). Entonces, la interacción de van der Waals que teníamos originalmente es reemplazada por unas interacciones dipolo-dipolo resonantes, lo que les hace que interactúen mucho más fuertemente que antes, y a distancias aún mayores: el bloqueo había sido causado por los átomos interactuando dentro de un polaritón, pero ahora los polaritones pueden interactuar entre sí. De modo que, cuando la potencia de las microondas es pequeña, estas interacciones son tan dominantes que previenen que podamos recuperar los fotones que habíamos almacenado, dispersándolos en otras direcciones. Sin embargo, si las microondas son lo suficientemente potentes, pueden prevaler frente a las interacciones resonantes y observaríamos las oscilaciones de nuevo.

Figura 3: Las oscilaciones inducidas entre dos estados Rydberg. La potencia de las microondas aumenta de izquierda a derecha. La linea intermitente muestra la transición entre la situación de “baja potencia” (dominada por las interacciones entre átomos Rydberg) a “alta potencia” (dominada por las microondas)

Este sistema es muy particular, y todavía no se comprende completamente. Aún queda mucho por hacer, tanto teórica como experimentalmente. Pero, aun así, podemos imaginarnos algunas aplicaciones. Si pudiésemos controlar las interacciones entre fotones individuales, sería posible construir puertas lógicas cuánticas que ayudarían en la construcción de computadores cuánticos ultrarrápidos, o usar criptografía cuántica

Además, existen ciertas similitudes en el modo en que los estados Rydberg pueden “saltar” entre polaritones, y el “salto” de las excitaciones en los complejos de captación de luz fotosintéticos en las plantas. Experimentos como estos podrían ayudar a modelar la fotosíntesis, o incluso ayudar a los científicos a diseñar células solares más eficientes.

Bibliography
[1] D. Maxwell, D. J. Szwer, D. Paredes-Barato, H. Busche, J. D. Pritchard, A. Gauguet, K. J. Weatherill, M. P. A. Jones, C. S. Adams, “Storage and Control of Optical Photons Using Rydberg Polaritons”. Physical Review Letters , 110, 103001 (2013). Abstract. [versión libre en el arXiv]
[2] Antoine Browaeys, “Viewpoint: Catch and Release of Photons”. Physics , 6, 25 (2013). Article.
[3] Nobel Prize in Physics 1997: Link.
[4] Thibault Peyronel, Ofer Firstenberg, Qi-Yu Liang, Sebastian Hofferberth, Alexey V. Gorshkov, Thomas Pohl, Mikhail D. Lukin, Vladan Vuletić, “Quantum nonlinear optics with single photons enabled by strongly interacting atoms”. Nature, 488, 57-60 (2012). Abstract.
[5] Y.O. Dudin,  A. Kuzmich, “Strongly Interacting Rydberg Excitations of a Cold Atomic Gas. Science”. 336, 887-889 (2012). Abstract.
[6] Alexios Beveratos, Rosa Brouri, Thierry Gacoin, André Villing, Jean-Philippe Poizat, and Philippe Grangier, “Single Photon Quantum Cryptography”. Physical Review Letters, 89, 187901 (2002). Abstract.
[7] Michel Orrit, “Photon Statistics in Single Molecule Experiments”. Single Molecules, 3, 255-265 (2002). Abstract.
[8] R. Hanbury Brown, R.Q.  Twiss, “Correlation between Photons in two Coherent Beams of Light”. Nature, 177, 27-29 (1956). Abstract.