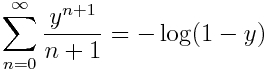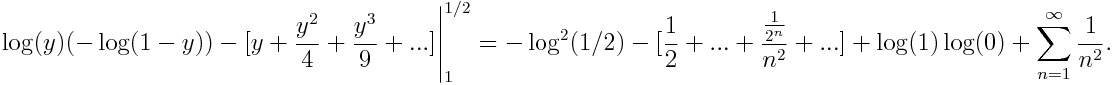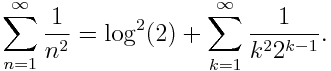Recientemente ha salido en Arxiv un artículo, de Thomas Hou y Zhen Lei, donde prueban singularidades para un modelo de las ecuaciones de Euler incompresibles tridimensionales. Este no es uno de los problemas del milenio, pero está íntimamente relacionado con uno de ellos. Me refiero al problema de la existencia de singularidades en las ecuaciones de Navier-Stokes incompresibles.
Las ecuaciones de Euler incompresibles representan las velocidades de un fluido incompresible y no viscoso. Podemos pensar en agua. Las ecuaciones de Navier-Stokes incompresibles representan las velocidades de un fluido incompresible y viscoso. Por lo tanto están más cerca de captar la realidad.
Veamos este video:
Durante los primeros segundos salen en pantalla un par de recipientes con dos fluidos distintos. Pues bien, las ecuaciones de Euler son una aproximación correcta al fluido de la izquierda, mientras que no lo son para el de la derecha debido a la enorme viscosidad que tiene. En este otro vídeo vemos otro efecto de la viscosidad: el fluido verde se “pega” al fondo del vaso.
Ahora bien, ¿qué significa que haya una singularidad en las ecuaciones de Euler? Bueno, estas ecuaciones (en el caso de un fluido homogéneo) son:
a) la conservación de momento: (3 ecuaciones)
b) la condición de incompresibilidad: (1 ecuación)
donde y
.
Viendo que el operador y
son derivadas un primer significado de la ecuación está claro: un campo de vectores
es solución de las ecuaciones de Euler incompresibles cuando sus derivadas satisfacen las ecuaciones anteriores en cada punto
del espacio para todo tiempo
.
Así, diremos que hay una singularidad cuando alguna o varias de estas derivadas no exista para algún punto del espacio en algún tiempo
. Por ejemplo, podemos pensar en la función
que no tiene derivada en el punto
.
Pues bien, la existencia de singularidades (o su inexistencia) es un tema central desde el punto de vista matemático y físico porque es crucial a la hora de derivar el modelo. Es decir, si no hubiese una solución para todo tiempo entonces es que las hipótesis de las que se derivan las ecuaciones NO se satisfacen y, por lo tanto, las ecuaciones no tienen sentido físico. Visto así, casi es un alivio, porque, o sabemos resolver las ecuaciones para todo tiempo o no tenemos que hacerlo.
Para acabar con esta entrada voy a dejar un enlace a una entrada previa sobre el resultado de Ángel Castro, Diego Córdoba, Charles Fefferman, Francisco Gancedo y Javier Gómez sobre las singularidades en las olas (observad que el agua en una ola sigue las ecuaciones de Euler). Estas singularidades en la superficie no son del mismo tipo de las comentadas en la entrada y por eso no las mencionamos más.
Probablemente, si saco algo de tiempo, escribiré alguna entrada sobre el modelo de Euler más sencillo que conozco, la ecuación de Burgers.
Nota: Esta entrada participa en el Carnaval de Matemáticas en su edición 3.141, que organiza el blog Desequilibrios.