En esta nueva entrada de la serie de las Paradojas (ver las otras entradas aquí ,
aquí y aquí) vamos a tratar de explicar paradojas que nacen de la mala interpretación de la probabilidad.
Todo el mundo conoce la serie C.S.I. y sus secuelas. En la serie un grupo de investigadores de la policía se dedican a buscar pruebas para resolver casos que sin el uso de avanzadas técnicas científicas y la participación de estos peritos forenses sería imposible solucionar. Los capítulos de la serie cuentan el asesinato y cómo los miembros del C.S.I. han recabado las pistas y acaban con la detención del culpable. Sin embargo hay una última parte que nunca tratan. Me refiero al juicio. Y es que, aunque tal cual está en la serie parece obvia la culpabilidad dadas las pruebas que se han encontrado, la valoración de las evidencias es un tema peliagudo en extremo.
El problema si lo escribimos de manera matemática involucra probabilidades condicionadas. La definición de este objeto (sacada de la wikipedia) es, dado un espacio de probabilidad  y dos eventos o sucesos
y dos eventos o sucesos 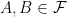 con
con 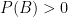 , la probabilidad condicional de ‘A’ dado ‘B’ está definida como:
, la probabilidad condicional de ‘A’ dado ‘B’ está definida como:
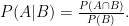
Hemos de pensar en B como en que ha ocurrido algo que modifica la información que tenemos disponible.
Así, si dado un caso de los de la serie de televisión, consideramos los sucesos
1) “se encuentran evidencias”. Este suceso se escribe E
2) “el sospechoso es culpable”. Este suceso se escribe C.
3) “el sospechoso es inocente”. Este suceso se escribe I.
4) “el sospechoso es inocente dado que hemos encontrado la prueba E”. Este suceso lo escribimos como  .
.
y
5) “el sospechoso es culpable dado que hemos encontrado la prueba E”. Este suceso lo denotamos por  .
.
Así la probabilidad que le interesa al juez con sobrecarga de trabajo que le toque es  o bien
o bien  .
.
Vamos a motivar nuestra nueva entrada sobre paradojas con un caso famosísimo en su época: el caso Dreyfus (ver esta página para más detalles). Esta novela por entregas tiene de todo, un bueno inocentón, el propio Dreyfus, un malo malísimo con multitud de problemas, Esterházy, y hasta cameos de personajes famosos como por ejemplo Zola. Un brevísimo resumen: tras la guerra franco-prusiana del siglo XIX se detectó una filtración en el ejército francés. Se detuvo al Capitán Alfred Dreyfus. Se tenía como principal evidencia una carta. Lo que ocurrió es que un “perito” estimó la probabilidad de coincidencia entre la letra de la carta y la letra del Capitán Dreyfus, suponiendo que Dreyfus fuese inocente, como 0.2. Como este mismo perito había observado 4 coincidencias y éstas se asumían independientes (es decir, que la probabilidad de las cuatro es el producto de las cuatro probabilidades) el perito conluyó que Dreyfus era culpable porque, según él, “la probabilidad de que fuese inocente dada la evidencia (las coincidencias entre la carta y la letra de Dreyfus) es muy pequeña”. El lector avispado se habrá dado cuenta del truco. El perito “estima” (que esa es otra cosa, ¿por qué la probabilidad es 0.2?) 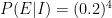 y entonces concluye que
y entonces concluye que 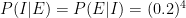 .
.
Veamos qué implicaciones tiene la asunción 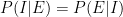 . Se tiene que
. Se tiene que
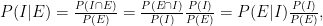
y, similarmente,

Ahora consideramos la cantidad

Si ahora usamos la hipotesis de que 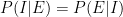 y
y  se concluye que
se concluye que
 lo que contradice la presunción de inocencia en casi todos los casos.
lo que contradice la presunción de inocencia en casi todos los casos.
¿Cuál es la moraleja? Pues que la probabilidad no es intuitiva nunca (o casi nunca) y que todos los argumentos probabilísticos deben ser cuidadosamente repasados. Si no lo hacemos así nos arriesgamos a repetir tristes historias (ver esta entrada de la wikipedia o esta otra).
–Referencias: 1) Estadística y Evaluación de la Evidencia para Expertos Forenses. Segunda Edición. C. Aitken y F. Taroni. (Traducido por: J. Lucena, L. Gil y R. Granero), Ed. Dykinson.
— Con esta entrada participamos en la edición 2.7 del Carnaval de Matemáticas, que está organizado por La Aventura de la Ciencia.
