Voy a escribir una serie de artículos que traten las diversas paradojas que hay; si no todas, al menos las más conocidas. Creo que es justo empezar con las de Zenón, al menos con algunas de ellas, ya que son las más antiguas de las que tengo constancia. También, porque es fácil ver donde está la argucia.

Zenón de Elea (ver aquí) intentaba demostrar que no podía haber movimiento, que este era sólo una ilusión. Para ello, propuso una serie de paradojas que “probaban” su punto de vista.

El veloz Aquiles compite contra una tortuga, la velocidad de Aquiles es doble que la de la tortuga, y éste, seguro de su victoria, le da ventaja.

Zenón razonaba lo siguiente, como la tortuga en el tiempo (cada vez más pequeño) que Aquiles se mueve se mueve a su vez (aunque sea un movimiento diminuto enseguida) Aquiles nunca la alcazará, pues siempre irá un épsilon por detrás.

Podemos resolver la paradoja de dos maneras, considerando series, y considerando espacios discretos. Por discretos quiero decir que Aquiles dé zancadas de longitud fija. La segunda no tiene interés, pues por la cuenta de la vieja sale fácil, además no enlaza tan bien como la otra para introducir conceptos (salvo que uno esté pensando ya en cuantización). Veamos como se resuelve con series.

A ver, si Aquiles le da 1 de ventaja a la tortuga, entonces cuando Aquiles va por su primer metro la tortuga va por 1.5, cuando Aquiles va por 1.5 la tortuga va por 1.75… Veamos cuanto recorre la tortuga. La tortuga en tiempo 0 está en 1, en tiempo 1 está en 1.5 y así sucesivamente, la tortuga recorre por lo tanto . Veamos lo que recorre Aquiles. Aquiles en tiempo 0 está en 0, pero su velocidad es doble, por lo que se tiene

.
Concluímos que Aquiles alcanza a la tortuga en
En este caso en particular, con estas velocidades, esta ventaja… estaba claro desde el principio: no había que meterse en follones de series, pues otra vez la cuenta de la vieja nos vale. En lugar de considerar tiempos cada ez más pequeños, consideremos los tiempo estándar del problema. En este caso si la tortuga avanza uno y Aquiles dos metros por segundo, y Aquiles le dió un metro de ventaja a la tortuga, entonces en un segundo la tortuga está en el metro 2, que es justamente donde está Aquiles.

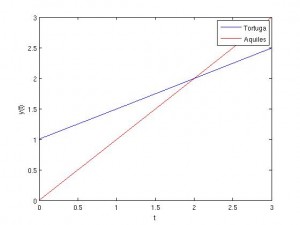
Veamos esto con un dibujo. La velocidad de la tortuga es 1/2 (en las unidades de Aquiles), y su posición inicial es y=1. Por lo tanto, tenemos que su posición en cada tiempo viene dada por la recta y=1+t/2. Para Aquiles tenemos que su velocidad es 1 (estamos usando sus unidades) y su posición inicial es y=0. Por lo tanto su recta es y=t. Comprobamos que en t=2 las rectas se cortan, por lo tanto Aquiles se encuentra con la tortuga.

Otra de las paradojas que Zenón utiliza es la la de la dicotomía

Aquello que se mueva entre dos puntos, ants de cubrir toda la distancia debe cubrir la mitad, y antes la mitad de la mitad…

Zenón argumentaba que al continuar hata el infinito no podía haber movimiento, pues necesitaría tiempo infinito. Ya hemos visto que usando series de desmontaba la anterior, y esta tiene la misma pinta, pues todo el problema es si la sucesión de tiempos me da una serie convergente, en cuyo caso, el valor de la suma será el tiempo empleado en movernos entre esos dos puntos.

Consideremos que avanzamos a velocidad fija de un metro por segundo entre el punto A y el B, separados por una distancia de un metro. En este caso tenemos que los tiempos que tardamos en recorrer las sucesivas ‘medias partes’ del recorrido es justamente la longitud del trozo en cuestión. Veamos, la sucesión de distancias recorridas es desde n=1 hasta el infinito. Es decir, en tiempo 1 hemos recorrido 0.5,… Si sumamos esta serie nos da 1, por lo tanto la suma de los tiempos (infinitos) da un número finito, por lo que el movimiento es posible. Otra vez los número están puestos para que podamos resolver el problema sin considerar series, pues ya sabíamos que tardaríamos uno.

¿Por qué hemos de considerar series aun en casos tan simples? pues porque lo importante, y lo que acaba de desmontar estas paradojas es el concepto de convergencia[negrita], la clave es que una suma de infinitas cosas bajo ciertas condiciones puede tener una suma finita.
Era eso lo que Zenón no tenía nada claro; él veía infinitos tiempos y decía: “no puede ser que nos movamos, pues tardaríamos un tiempo infinito”.

Hemos desmontado 2 de las paradojas de Zenón. Dejaremos para otro post una manera de desmontar la tercera paradoja, pues para ello necesitamos saber que existen distintos tipos de infinitos.
En las próximas entradas de esta serie, veremos más paradojas y cómo evitarlas (si se puede).