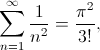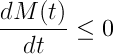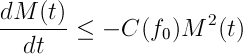El concepto de limite es una herramienta fundamental, quizá la más útil e importante de todas las matemáticas. Historicamente diría que el primer límite de la historia lo calculó Arquímedes, haciendo la primera integración. Veamos cómo:
En la época estaban interesados en calcular áreas delimitadas por curvas. Es un problema grande, que enlaza con el cálculo de 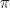 . Arquímedes consideró un segmento de parábola y el área que encierra. Para calcular el área dijo, bueno, si sé calcular el área de triángulos, entonces lo que tengo que hacer es ‘tapar’ el segmento de parábola con triángulos. Esto hizo, y observo que los trozos que quedabas sin tapar en realidad volvías a ser segmentos de parábola, por lo que se podría repetir. Así llegó a una serie geométrica de razón un cuarto INFINITA. También es la primera vez que se suma una serie infinita.
. Arquímedes consideró un segmento de parábola y el área que encierra. Para calcular el área dijo, bueno, si sé calcular el área de triángulos, entonces lo que tengo que hacer es ‘tapar’ el segmento de parábola con triángulos. Esto hizo, y observo que los trozos que quedabas sin tapar en realidad volvías a ser segmentos de parábola, por lo que se podría repetir. Así llegó a una serie geométrica de razón un cuarto INFINITA. También es la primera vez que se suma una serie infinita.
Veamos otro ejemplo del método. Arquímedes quería calcular 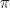 . Entonces lo que hace es considerar un círculo de radio uno. Su área es
. Entonces lo que hace es considerar un círculo de radio uno. Su área es 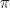 . Ahora veis por donde va. Como sabe calcular áreas de polígonos ‘tapa’ con hexágonos el círculo. Razona que si el hexágono está fuera, entonces el área será mayor, mientras que si el círculo tapa al hexágono será menor. Obviamente tanto los hexágonos como el círculo son concéntricos. Ahora el límite viene al hacer crecer el número de lados, con lo que ambas aproximaciones a
. Ahora veis por donde va. Como sabe calcular áreas de polígonos ‘tapa’ con hexágonos el círculo. Razona que si el hexágono está fuera, entonces el área será mayor, mientras que si el círculo tapa al hexágono será menor. Obviamente tanto los hexágonos como el círculo son concéntricos. Ahora el límite viene al hacer crecer el número de lados, con lo que ambas aproximaciones a 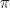 (por arriba y por abajo) se van haciendo más y más precisas. Este proceso en el límite te da
(por arriba y por abajo) se van haciendo más y más precisas. Este proceso en el límite te da 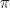 sin ningún error, pero en la ‘práctica’ te lo da con el error que tu quieras. Digamos que hay un cambio filosófico entre ambas afirmaciones. Aquí podríamos hablar de cómo afecta la noción de observable físico a esto, hasta qué punto debemos preguntarnos por LA realidad y hasta donde sobre LA PARTE de realidad que podemos conocer. Concluimos diciendo que un ordenador, usando Matlab, si no se le dan instrucciones específicas tiene 16 decimales guardados. Con este método y paciencia podríamos acercarnos tanto a
sin ningún error, pero en la ‘práctica’ te lo da con el error que tu quieras. Digamos que hay un cambio filosófico entre ambas afirmaciones. Aquí podríamos hablar de cómo afecta la noción de observable físico a esto, hasta qué punto debemos preguntarnos por LA realidad y hasta donde sobre LA PARTE de realidad que podemos conocer. Concluimos diciendo que un ordenador, usando Matlab, si no se le dan instrucciones específicas tiene 16 decimales guardados. Con este método y paciencia podríamos acercarnos tanto a 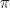 que engañásemos al ordenador.
que engañásemos al ordenador.
Esto es en cuanto a límites e integrabilidad. Para la derivabilidad es lo mismo.
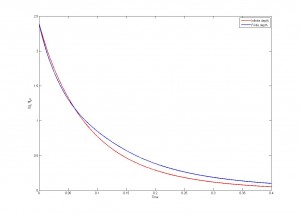
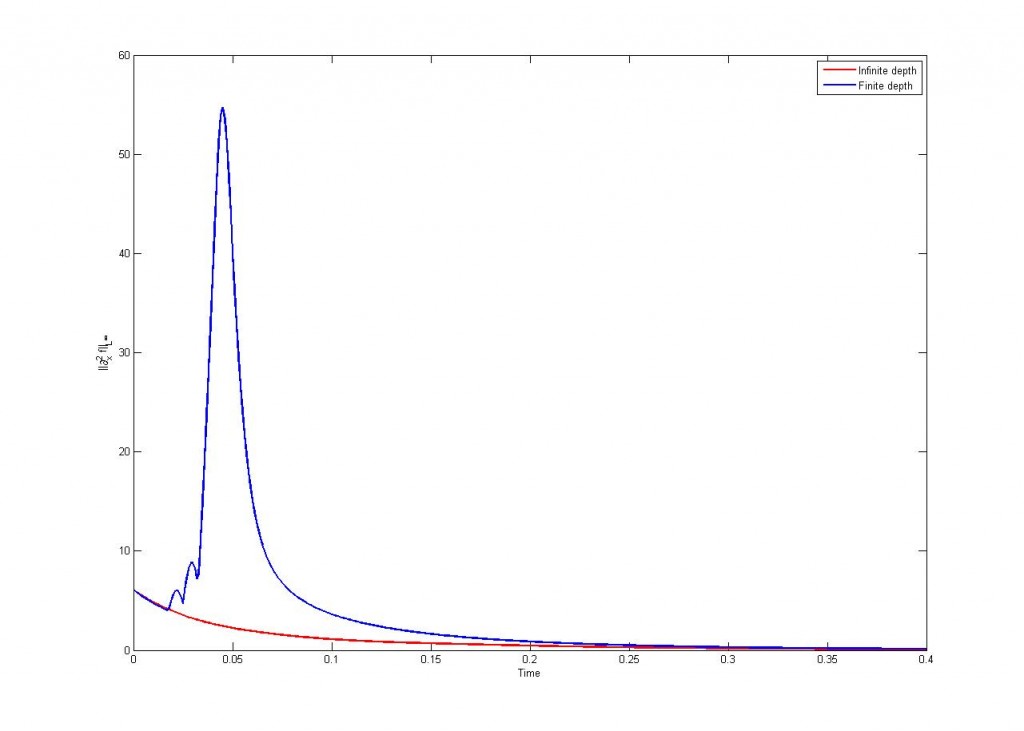
Tenemos una función y vamos trazando secantes entre dos puntos, ahora tomamos el límite cuando un punto se acerca al otro. Así obtenemos la tangente. Entonces, cuando hacemos cálculo numérico, y queremos estimar una derivada, por ejemplo en problemas de transferencia de calor, lo que hacemos es considerar una ‘diferencia finita’, esto es un cociente como los de la definición de derivada, pero con un pasito pequeño, sin tender al límite.  con h pequeño.
con h pequeño.
Veamos un último caso de la importancia de los límites, este más bien modesto, sólo trataremos con los números.
¿Alguien se ha preguntado cómo se definen los números? Bueno el proceso axiomático es el siguiente. Se definen los naturales por medio de los axiomas de Peano. Después con una relación de equivalencia y apoyándonos en los naturales definimos los enteros. Ahora los racionales vienen de los enteros con una relación de equivalencia parecida. ¿Y los reales?. Aquí el método no funciona. Los reales no se definen con ninguna relación de equivalencia como las anteriores, sino que se definen para ‘completar’ (uno que sepa más que las mates básicas se dará cuenta de que no debería haber comillas). Veamos un ejemplo de lo que quiero decir. Sabemos desde lo que hizo el pobrecillo de Hipaso de Metaponto que raíz de dos es irracional, por lo tanto no estará en los racionales. Sin embargo, hay racionales tan cerca como queramos, por ejemplo la sucesión 1.4,1.41,… (cada vez añadimos una cifra de la expansión decimal de raíz de dos) tiende a raíz de dos. Entonces si hubiese justicia en el mundo deberíamos considerar un conjunto mayor de números (los reales) donde si una sucesión contenida tiende a un número este número también esté en el conjunto. Así se definen los reales, como el límite de las sucesión de racionales.
Menuda parrafada. Pero, ¿a qué viene esto? Bueno, es que me he percatado de que en ocasiones se da una definición intuitiva pero errónea. La susodicha definición en el caso de una sucesión es:
Se dice que una sucesión tiene límite L si al tomar sucesivos términos de la sucesión nos vamos acercando a L.
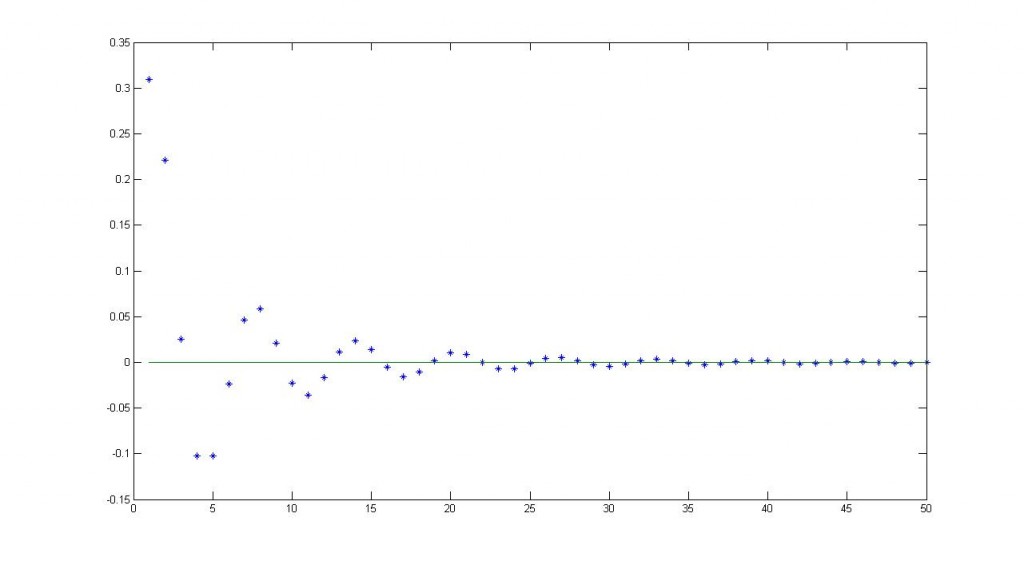
Ahí van dos contradicciones que se me ocurren rápido. Sea la sucesión dada por 0.9, 0.99, 0.99, 0.999… Si hacemos caso de la definición anterior el límite sería 1000, porque cada vez estoy más cerca de ese número. ¡Anda, pero si también vale con 100!. Entonces el límite así definido ni siquiera es único. Por cierto, el verdadero límite es 1, como veremos luego.
Veamos la definición correcta.
Se dice que una sucesión  tiene límite a si para todo
tiene límite a si para todo  (DADO) se tiene que existe un
(DADO) se tiene que existe un 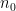 tal que para todo
tal que para todo 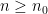 se cumple
se cumple  .
.
Veamos qué dice esto tan raro. Pensemos en nuestra recta real, donde marcamos unas cruces en los números que estén en nuestra sucesión. Entonces DADO un número POSITIVO (es una distancia)  lo que ha de ocurrir es que todos los términos de la sucesión a partir de uno
lo que ha de ocurrir es que todos los términos de la sucesión a partir de uno  estén a una distancia menor que
estén a una distancia menor que  de a. O lo que es lo mismo, que estén entre
de a. O lo que es lo mismo, que estén entre  y
y  . O lo que es lo mismo, que en a podamos poner una bola de radio
. O lo que es lo mismo, que en a podamos poner una bola de radio  y de manera que nos tape siempre un número infinito de términos de la sucesión, o lo que es lo mismo, que deje fuera sólo un número finito. Es muy importante observar que esto ha de cumplirse para todo
y de manera que nos tape siempre un número infinito de términos de la sucesión, o lo que es lo mismo, que deje fuera sólo un número finito. Es muy importante observar que esto ha de cumplirse para todo  .
.
Veamos unos ejemplos.
La misma sucesión de antes, 0.9, 0.99… Supongamos que el límite es 1000, entonces elegimos 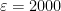 . Se cumple que tapamos a nuestra sucesión, ¿dónde está el problema?. La contradicción viene en el PARA TODO
. Se cumple que tapamos a nuestra sucesión, ¿dónde está el problema?. La contradicción viene en el PARA TODO  . Si elegimos en lugar de
. Si elegimos en lugar de 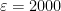 lo elegimos
lo elegimos  ya no se cumple. Supongamos ahora que el límite es 1. Elegimos
ya no se cumple. Supongamos ahora que el límite es 1. Elegimos 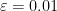 . Entonces se tiene que nuestra ‘bola’ tapa a todos los elementos menos a uno de la sucesión. Esto, como hemos visto antes no demuestra que el límite sea 1. Elijamos otro
. Entonces se tiene que nuestra ‘bola’ tapa a todos los elementos menos a uno de la sucesión. Esto, como hemos visto antes no demuestra que el límite sea 1. Elijamos otro  , por ejemplo, 0.001. Podemos repetir lo anterior. Vamos a por el caso general. Ánimo. Sea
, por ejemplo, 0.001. Podemos repetir lo anterior. Vamos a por el caso general. Ánimo. Sea  fijo. Entonces debemos calcular nuestro
fijo. Entonces debemos calcular nuestro 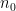 . Se tiene
. Se tiene  siempre que
siempre que ![n_0>[log_{10}( \varepsilon)] n_0>[log_{10}( \varepsilon)]](http://s0.wp.com/latex.php?latex=n_0%3E%5Blog_%7B10%7D%28+%5Cvarepsilon%29%5D&bg=T&fg=000000&s=0) .
.
Varias observaciones:
1) Nuestro 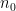 en realidad depende de varias cosas. Se tiene
en realidad depende de varias cosas. Se tiene 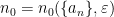 . Es decir, lo normal es que, fija la sucesión, cuanto más pequeño sea nuestro
. Es decir, lo normal es que, fija la sucesión, cuanto más pequeño sea nuestro  más grande tenga que ser nuestro
más grande tenga que ser nuestro 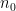 .
.