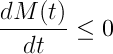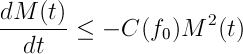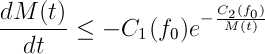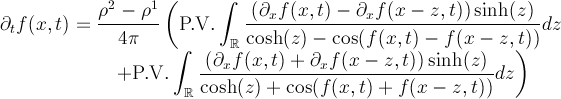En este blog sabéis que periódicamente ponemos entradas de física, o mejor aún, de cómo las matemáticas se utilizan para explicar cosas de física (ver por ejemplo ésta, ésta y ésta otra entrada). La que colgamos hoy es de esas. Además ésta estaba pendiente porque en una entrada sobre varios modelos de las ecuaciones de Euler dije que iba a escribir sobre la ecuación de Burgers. Pues bien, aquí está.
La ecuación de Burgers no viscosa (que toma su nombre de J.M. Burgers) se escribe de la siguiente manera
Se trata de una ecuación de primer orden no lineal y suele ser el primer ejemplo de ecuación no lineal que se pone en los libros de texto (para una lectura rápida sobre las propiedades de algunas ecuaciones en derivadas parciales sencillas leed esto). Se trata además de la primera ecuación que surge de manera natural cuando uno quiere entender las ecuaciones de Euler y también “refleja” (más o menos) el comportamiento de una ola (ver un artículo reciente sobre este tipo de ecuaciones aquí).
Si pasamos esquivando el cuestión de la existencia o no de solución para dicho problema (1) y directamente suponemos que existe tal solución y que además es una función “suave”, i.e., con tantas derivadas como nos hagan falta, podemos obtener una propiedad importante de manera muy sencilla. Supongamos que tenemos una solución que tiene, al menos, dos derivadas en
, y supongamos además que dicha solución se va muy rápido a cero cuando
se hace muy grande. Dicha solución tendrá un mínimo (o ínfimo), y un máximo (o supremo) y sus posiciones dependerán del tiempo. Como la función tiende a cero en el infinito estos valores se alcanzan (es decir, no son ínfimos/supremos). Denotemos el punto donde
alcanza su mínimo como
y el punto donde
alcanza su máximo como
. Por lo tanto, fijo
,
y
y
y obtenemos que tanto el máximo como el mínimo del dato inicial se conservan,
y
Si ahora repetimos el argumento para la evolución de obtenemos, si
es el punto de mínimo, la siguiente ecuación
Ahora observamos que (2) es una EDO que se puede resolver explícitamente (¿sabrías cómo hacerlo?)
y tenemos que, si ,
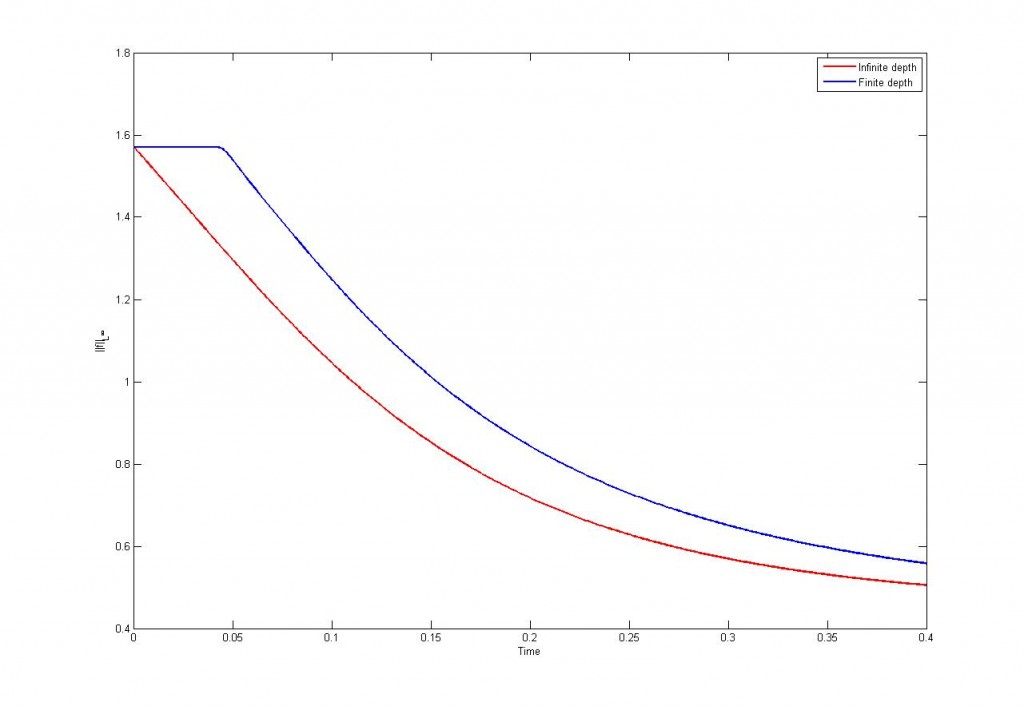
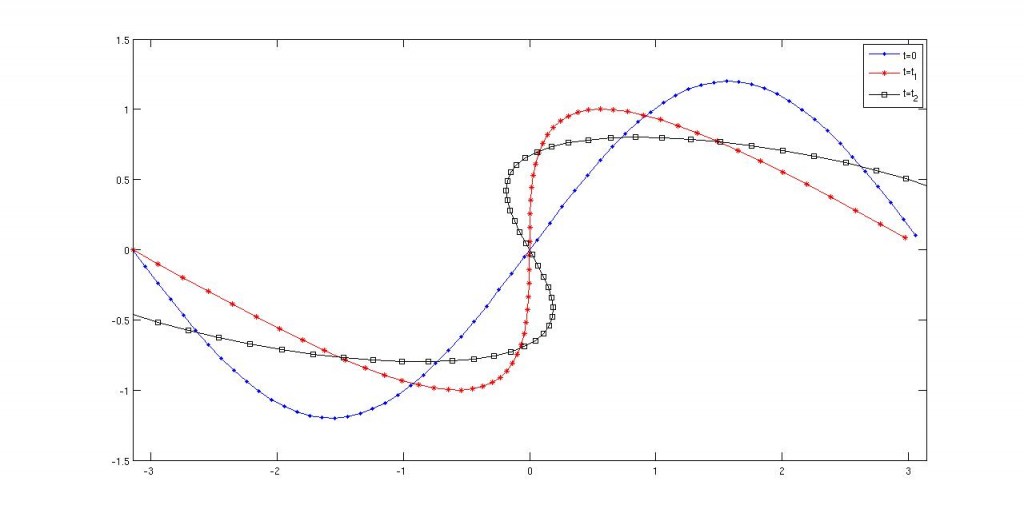
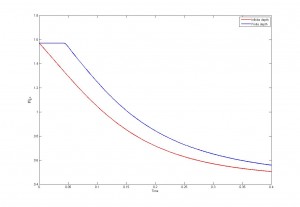
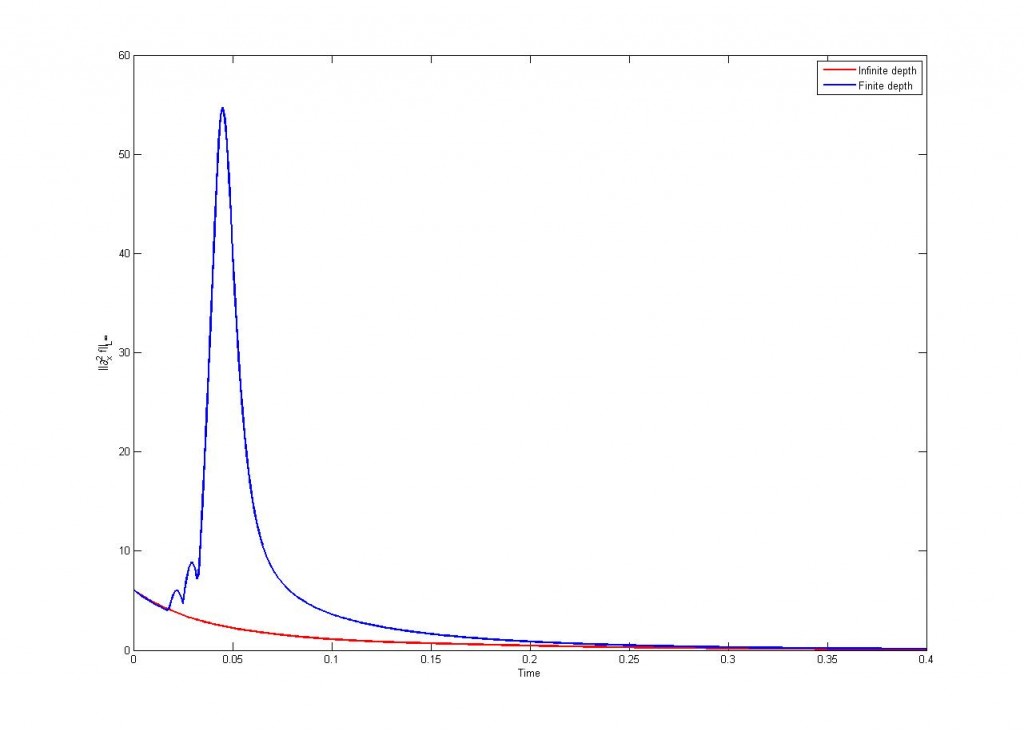
Veamos unas simulaciones para entender bien lo que pasa aquí:
Esto es un ejemplo de singularidad. Tampoco debería sorprendernos, pues esta ecuación aparece relacionada con olas y parece reflejar el hecho de que las olas “rompen”.
¿Qué pasa si ahora añadimos una pequeña viscosidad con la forma de un laplaciano? (Esta difusión puede generalizarse, por ejemplo como en [2])
Esta ecuación se conoce como Ecuación de Burgers viscosa y puede entenderse como un modelo (en realidad una caricatura) de la ecuación de Navier-Stokes. Bueno, ahora la cuenta anterior no es tan sencilla, porque el término difusivo, el laplaciano, tiene signo “bueno”, es decir, se opone a los crecimientos descontrolados como los que se veían en el vídeo anterior. De hecho, usando la transformación de Cole-Hopf (ver aquí) se puede ver que esta ecuación tiene existencia global para cualquier valor de .
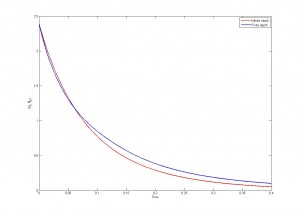
De esta manera, el vídeo ahora es
–Referencias:
1) Vincent Duchene, “Decoupled and unidirectional asymptotic models for the propagation of internal waves”, preprint Arxiv, http://arxiv.org/abs/1208.6394.
2) RGB y José Manuel Moreno, “La ecuación de Burgers como un paso previo al estudio de los fluidos incompresibles”, La Gaceta de la RSME, vol 15, num 3, pag, 489-512, 2012. ArXiv preprint http://arxiv.org/abs/1105.5990.
–Nota: Como lo de aproximar soluciones de EDPs es algo muy útil, dedicaremos una entrada próximamente a un método sencillo que produce muy buenos resultados.