Category Archives: Ecuaciones diferenciales
De cuerdas y tambores, o cómo la física aparece en un problema de matemáticas
A Francisco Gancedo le conceden el premio “Real Maestranza de Caballería de Sevilla”
¿Cómo empezar bien el año? Pues recibiendo un premio. Esa ha sido la manera de comenzar el 2012 de Francisco Gancedo ya que la Real Academia Sevillana de Ciencias le ha concedido el premio “Real Maestranza de Caballería de Sevilla” por sus investigaciones en el estudio de problemas de frontera libre asociados a interfases entre fluidos incompresibles. O de otra manera: olas en diversas situaciones (puede leerse una entrada sobre el tema aquí).
¡Felicidades Paco!
Usando las Matemáticas en biología
Diego Córdoba es el nuevo Premio “Miguel Catalán”
El otro día, el Martes pasado concretamente, se anunciaron los Premios “Miguel Catalán”. Estos premios los da la Comunidad de Madrid al investigador más sobresaliente de todas las ciencias y tenemos el gusto de anunciar que el Premio en la categoría Jóven se lo ha llevado Diego Córdoba Gazolaz por sus trabajos en Mecánica de Fluidos. Algunos de los resultados en los que ha participado ya han sido anunciados aquí.
Nuestra más sincera enhorabuena desde aquí.
Introducción al cálculo variacional en las matemáticas
Esta entrada es la gemela de la entrada Introducción al cálculo variacional en la física (http://scientiapotentiaest.ambages.es/?p=87). En ella David nos decía
Queremos saber qué camino tomará un cuerpo en una cierta situación. Imaginemos que tenemos una cantidad (un funcional, matemáticamente hablando), a la que llamaremos acción (con unidades de energía por segundo), que depende del “camino” que ese cuerpo toma en su movimiento. Esa acción puede ser calculada para cada cualquier camino siempre y cuando tenga una cierta regularidad. Pues bien, el camino real, el que tomará el cuerpo y que podrá ser predicho, es aquel que hace de la acción un mínimo (más rigurosamente, un valor estacionario).
Así, el enfoque en mecánica clásica es: dado un sistema físico, obtenemos un funcional; a este funcional se le calculan los puntos críticos y esos puntos críticos nos dan las soluciones del problema. Matemáticamente esto es ir del funcional a la ecuación diferencial.
Veamos esto con un ejemplo: Supongamos que tenemos una partícula de masa unidad bajo el influjo de un potencial (sistema físico).
Entonces el Lagrangiano se define como
donde es energía cinética, que depende de la velocidad
; y
es energía potencial, que depende del potencial
en el lugar donde la particula se encuentra. Entonces se tiene, si la posición de la partícula se denota como
, que el lagrangiano es
Ahora definimos la acción como Esta acción la hemos obtenido de consideraciones físicas como son la definición de energía cinética y potencial.
Una vez tenemos la acción, queremos minimizarla. Para esto hemos de encontrar los puntos críticos. Si fuese una función de una variable normal y corriente derivaríamos e igualaríamos a 0. Derivar es encontrar el cambio de una cantidad cuando se varía otra de manera infinitesimal. Aquí la idea es similar. Lo que hacemos es, dada una perturbación con los extremos fijos ( tal que
) de nuestra trayectoria
consideramos la curva
Ahora pensamos la acción para esta nueva curva como una función de
,
,
y obtenemos el cambio en ella cuando variamos ligeramente s; esto es, derivamos en y hacemos
.
Calculamos, utilizando la regla de la cadena,
(para el potencial)
(para la energía cinética).
Sustituyendo obtenemos y si integramos por partes en la primera integral nos queda
Esta integral debe ser 0 para que nuestra sea un punto crítico del funcional, y además debe serlo para toda perturbación
.
Estas consideraciones nos imponen una relación entre las derivadas y
,
que es, nada más y nada menos, la segunda ley de Newton.
Este enfoque va desde el funcional, que se obtiene con consideraciones físicas, a la ecuación diferencial. O de otra manera, se usa una ecuación diferencial para solucionar un problema de minimizar un funcional.
Sin embargo también existe el método inverso. Supongamos que tenemos una ecuación diferencial (generalmente en derivadas parciales) como puede ser
con una función no lineal, por ejemplo un polinomio. Así, el llamado Método Directo del Cálculo de Variaciones consiste en definir un funcional tal que sus puntos críticos vengan dados por la ecuación que era nuestro problema original.
Demostrar la existencia de solución para la ecuación original es lo mismo que conseguir un punto crítico de nuestro funcional. Si además probamos que es único entonces la ecuación tendrá una única solución. Así con este enfoque vamos desde la ecuación al funcional.
Y como seguir abundando en este tema puede ser muy técnico lo dejaremos aquí por el momento.
Las olas: Un matemático en la playa.
Ya va haciendo calor y empieza a apetecer el irse a la piscina o a la playa. Sin duda la playa es uno de los sitios menos entendidos por el mundo científico y más visitados por el resto del mundo. El fenómeno al que me refiero cuando digo que no se comprende completamente, claro está, son las olas. En esta entrada estudiaremos diversos casos de olas entre fluidos ilustrando el texto con diversos videos.
[iframe: width=”400″ height=”320″ src=”http://www.youtube.com/embed/GEl-Qu7ApGQ” frameborder=”0″ allowfullscreen]Vamos a empezar hablando de un caso un poco más general que las típicas olas en la superficie del mar. En matemáticas entendemos por interfase entre fluidos a la parte donde estos entran en contacto entre sí. Así una ola es la interfase entre el aire y el agua. Una interfase entre fluidos con distintas propiedades puede exhibir un comportamiento muy complicado, patológico si se quiere, pero que es, pienso yo al menos, visualmente muy bonito. Estoy pensando por ejemplo en singularidades como pueden ser las llamadas singularidades de Kelvin-Helmholtz o Rayleigh-Taylor. Hagamos una parada antes de proseguir con nuestras olas.
Supongamos por un momento que tenemos dos fluidos con densidades distintas, por fijar ideas digamos aceite y agua, de manera que el fluido más denso (el agua) está en el fondo de un recipiente cerrado completamente (un tubo con ambos extremos taponados). El fluido menos denso (el aceite) reposa encima del agua. Supongamos ahora que dicho tubo, y por tanto los fluidos, está en reposo, por ejemplo en una mesa. La pregunta es ¿qué ocurre si, repentinamente, inclinamos dicho recipiente? Veamos unos vídeos con este experimento:
[iframe: width=”400″ height=”320″ src=”http://www.youtube.com/embed/CL7s8h7mtPE” frameborder=”0″ allowfullscreen] [iframe: width=”400″ height=”320″ src=”http://www.youtube.com/embed/ggEp4n6Bhps” frameborder=”0″ allowfullscreen] [iframe: width=”400″ height=”320″ src=”http://www.youtube.com/embed/1XqJJfw63zQ” frameborder=”0″ allowfullscreen]Lo que vemos en el video es que la interfase “se enrolla” sobre sí misma. Esto es debido a que las velocidades (que son un vector en 3D) tangentes a la interfase tienen signo distinto. Es decir, si lo pensamos en una interfase en 2D (una curva) sería que la velocidad en el fluido que está encima de la interfase “señala hacia la izquierda” mientras que para el fluido que está debajo de la interfase “señala a la derecha”. De ahí esa tendencia a girar y enrollarse.
Supongamos ahora que cambiamos el orden de los fluidos. Ahora tenemos (por ejemplo porque tenemos una barrera entre ambos fluidos) el agua reposando sobre el aceite. ¿Qué ocurre si retiramos rápidamente la barrera entre ambos fluidos? Bueno, pues que el fluido más denso, por la gravedad, caerá hacía abajo, empujando en su camino al fluido menos denso, que subirá hacía arriba. Vale, el caso es que lo que va a ocurrir es sencillo de vaticinar, lo curioso aquí es la manera en que ocurre. Vayamos otro rato a youtube…
[iframe: width=”400″ height=”320″ src=”http://www.youtube.com/embed/VlAzyVx7N9M” frameborder=”0″ allowfullscreen] [iframe: width=”400″ height=”320″ src=”http://www.youtube.com/embed/8EkFL-8wIUI” frameborder=”0″ allowfullscreen]Tras ver estos experimentos y haber pensado un poquito nos damos cuenta de que el que quiera entender bien estos procesos tiene mucho trabajo por delante. Y ahí estamos bregando algunos…
Volvamos a las olas. Hace tan sólo unos días uno de mis jefes (Diego Córdoba) y algunos de mis compañeros (Ángel Castro, Francisco Gancedo y Javier Gómez) y otros colaboradores (el medallista Field Charles Fefferman) hicieron un importante avance. Probaron la existencia de otro tipo de singularidad para el caso de las olas. Bautizaron a esta singularidad como “splash”. Arremanguémonos y veamos un poco las matemáticas que hay debajo de todo esto…
Consideremos una curva en el plano. Esta será nuestra ola inicial. La evolucion de esta ola viene dada por la evolución del fluido bajo ella. Se trata así de un problema de frontera libre, es decir, donde el propio dominio es una incógnita. Así tenemos que, bajo la ola, se verifican las ecuaciones de Euler incompresibles y que además el fluido es irrotacional. Sobre la curva suponemos que tenemos el vacío (esto es un buen modelo porque el agua tiene una densidad mucho mayor a la del aire). Lo que se sabía antes de los trabajos de Diego y compañía eran la existencia local de solución, es decir, que una ola “suave” sigue siendo una ola “suave” al menos un corto tiempo. Esta existencia local es cierta tanto en el caso donde se supone que la profundidad del mar es infinita como en el caso con un lecho marino predeterminado (son resultados de S. Wu y D. Lannes, respectivamente). También se sabe que si las olas “son muy planitas” la existencia es global, es decir, la ola existe para cualquier tiempo (resultados obtenidos independientemente por S. Wu y P. Germain, N. Masmoudi y J. Shatah).
[iframe: width=”400″ height=”320″ src=”http://www.youtube.com/embed/SdPI6yrjJoM” frameborder=”0″ allowfullscreen]Los resultados con bandera española en este tema comienzan con un artículo (de A. Castro, D. Córdoba, C. Fefferman, F. Gancedo y M. López) donde se prueba que una ola que empieza siendo un grafo, es decir, se puede escribir como , deja en un tiempo finito
de ser un grafo. De otra manera, la ola rompe. Matemáticamente esto es que la derivada espacial de la ola se hace infinita en algún punto. El resultado de hace unos días que he mencionado más arriba abunda más en esta línea. Lo que A. Castro, D. Córdoba, C. Fefferman, F. Gancedo y J. Gómez prueban es que existen olas que empiezan siendo curvas suaves y que en un tiempo finito se tocan. Es decir, se ha perdido la propiedad de ser una curva sin autointersecciones. Así es plausible el escenario de comenzar con un grafo, evolucionar hasta perder la propiedad de ser un grafo, es decir, la ola rompe, y, al continuar pasando el tiempo, la curva se acabe autointersecando. Esto es justamente lo que hemos visto en el primer video de esta entrada. Así que podemos concluir dos cosas: una es que algo tan cotidiando como una ola puede ser matemáticamente un problema muy difícil. La segunda cosa que podemos aprender es que nuestro modelo para la dinámica de fluidos funciona en el sentido de que recupera comportamientos reales observados en la naturaleza.
Antes de acabar quiero agradecer a mi compañero Javier Gómez que nos haya dejado el video de sus simulaciones.
—-Esta es nuestra contribución a la edición 2.5 del Carnaval de Matemáticas (http://carnavaldematematicas.bligoo.es/), que está siendo albergado por el blog Juegos Topológicos (http://topologia.wordpress.com/d).
Cuántica e incertidumbre (Parte I)

Werner Heisenberg, uno de los padres de la Mecánica Cuántica
¿Qué es exactamente una EDO?
A lo largo de las entradas de esta bitácora han ido apareciendo conceptos relativamente avanzados (ecuaciones en derivadas parciales…) sin mencionar casi los conceptos previos (previos en el sentido pedagógico, porque cronológicamente surge todo al mismo tiempo) como pueden ser las ecuaciones diferenciales ordinarias.
Una ecuación diferencial ordinaria (EDO a partir de ahora) es una expresión que relaciona la derivada de la función incógnita con la propia función. Así el problema queda reducido a ver si podemos encontrar (o demostrar que existe) una función tal que se verifique una relación más o menos complicada entre ella y sus tasas de cambio.
Un ejemplo lo tenemos en la Ley de Malthus. Supongamos que tenemos un número de insectos . El incremento del número de insectos evolucionará de manera proporcional a el mismo, o de otra manera, en ausencia de rivales o limitaciones propias del medio la cantidad de hijos que medran es proporcional al número de padres. Razonable, ¿verdad?. Así la EDO la podemos escribir como
.
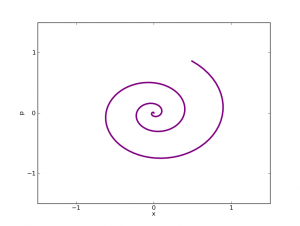
Unos comentarios antes de seguir: el número de datos iniciales (como en el ejemplo anterior) tiene que ser el mismo que el máximo número de derivadas presentes en la expresión. Así como la ecuación anterior tenía una derivada debíamos poner un dato inicial. En el ejemplo del oscilador armónico al tener la ecuación
necesitamos dos datos iniciales,
y
. Supongamos que tenemos una EDO de segundo orden (es decir, con dos derivadas) como la del oscilador armónico, entonces la solución general se escribe como $latex f(t)= c_1 e^{omega t}+ c_2e^{-omega t}$, donde para
son dos constantes que se fijan usando los datos iniciales. Es decir, el conjunto de soluciones de una EDO linear de segundo orden (sin usar los datos iniciales) es un espacio vectorial (gracias a la linearidad) de dimensión 2 (el número de derivadas). Esta es una diferencia fundamental (y poco conocida entre los físicos) con respecto a las EDPs, pues una EDP tiene un espacio de soluciones de dimensión infinita.
Parece claro que conseguir escribir la solución de una EDO de manera explícita, es decir, una fórmula cerrada, no va a ser fácil o siquiera posible en cuanto la EDO sea no-lineal, por ejemplo algo como . Nos interesa entonces saber que existe dicha solución, ser capaces de simularla con el ordenador y ser capaces de extraer propiedades cualitativas.
Para una EDO general, , la existencia se puede segurar si se dan unas propiedades en la expresión
, a saber, que sea derivable en la variable
.
Para aproximar la solución de la EDO se tienen que aproximar unas integrales,
. Según el método que usemos tendremos una mejor o peor cota del error cometido. La manera típica, conocida como métodos Runge-Kutta, de hacerlo es considerar una serie de puntos entre dos nodos temporales y calcular el valor de la función F en esos puntos. Después hemos de sumar dichos valores con unos pesos. La teoría de los métodos Runge-Kutta es bien conocida y se puede encontrar en la red sin mucho problema (siempre que se hable un mínimo de inglés al menos). Aquí voy a colgar unos códigos hecho por mí:
function [u,t,h,totalt]=euler(F,t0,T,u0,N)
%funcion que aproxima con un metodo de Euler explicito la solucion de la edo
%u’=F(u,t) hasta tiempo T con N nodos temporales. u0 es el dato inicial.
%%Rafael Granero Belinchon
tic
h=(T-t0)/N;
t=[t0:h:T];
u=zeros(N+1,1);
u(1)=u0;
for i=2:N+1
u(i)=u(i-1)+feval(F,u(i-1),t(i-1))*h;
end
plot(t,u);
totalt=toc;function [u,t,h,totalt]=rungekutta4(F,t0,T,u0,N)
%Funcion que aproxima con una RK4 la solucion de
%y’=F(y) y(t0)=u0 y tiempo final T. N da el numero
%de nodos temporales.
%%Rafael Granero Belinchon
tic
h=(T-t0)/N;
t=[t0:h:T];
u=zeros(N+1,1);
u(1)=u0;
for i=2:N+1
s1=feval(F,u(i-1),t(i-1));
s2=feval(F,u(i-1)+h*0.5*s1,t(i-1)+h*0.5);
s3=feval(F,u(i-1)+h*0.5*s2,t(i-1)+h*0.5);
s4=feval(F,u(i-1)+h*s3,t(i-1)+h);
u(i)=u(i-1)+(s1+2*s2+2*s3+s4)*h/6;
end
plot(t,u);
totalt=toc;function [u,t,totalt]=rungepasovariable(F,t0,T,u0,N,tol)
%funcion que aproxima con un metodo de paso variable
%la solucion de la ecuacion diferencial y’=F(y) en [t0,T]
%con u0 como dato inicial una cantidad N de pasos temporales y una tolerancia tol.
%%Rafael Granero Belinchon
tic
t=[t0];
dt=(T-t0)/N;
u=[u0];
u1=u;
u2=u;
while t(end)<=T
fev=feval(F,u(end),t(end));
s=u(end)+0.5*dt*fev;
u2(end+1)=u(end)+feval(F,s,t(end)+0.5*dt)*dt;
u1(end+1)=u(end)+fev*dt;
err=abs(u2(end)-u1(end));
h=0.9*dt*sqrt(tol/err);
u(end+1)=u(end)+feval(F,s,t(end)+0.5*h)*h;
t(end+1)=t(end)+h;
dt=h;
end
totalt=toc;
Caminos aleatorios e imágenes
Esta es nuestra entrada para el Carnaval de Matemáticas 2.2 (alojado esta vez en Gaussianos).
Muchas veces se ha escrito sobre la relación entre los caminos aleatorios y la ecuación del calor, y quizá próximamente tratemos nosotros ese tema. Sin embargo hoy vamos a ver una aplicación poco conocida de esa relación. En esta entrada vamos a tratar brevemente una manera de emplear las matemáticas, y mas concretamente los caminos aleatorios o las trayectorias brownianas, para que un ordenador sepa qué imagen está ‘viendo’. Ahora que han puesto unos radares de tramo (que funcionan memorizando las matrículas de los coches y midiendo tiempos para calcular la velocidad media del tramo donde está el radar) en las carreteras españolas este problema tiene una clara aplicación práctica.
Desde hace unos años el tratamiento de imágenes usando ecuaciones en derivadas parciales es un área de investigación matemática floreciente. Normalmente tratan el problema de detectar los contornos de una imagen o de suavizarlos (de manera que veamos mejor la imagen). Nuestro problema es ligeramente distinto. Nosotros, dada una silueta (es decir un contorno cerrado y suave que encierra un área negra mientras que lo de fuera es blanco), tenemos que enseñar al ordenador a sacar propiedades de los contornos de manera que aprenda a distinguir entre las distintas siluetas.
La manera usual de extraer propiedades de una silueta es ‘medir’ y ‘clasificar’ los puntos del interior del contorno en función de su posición relativa a la curva que delimita la silueta (a partir de ahora la denotaremos S, mientras que el contorno será ). Esto puede hacerse por ejemplo con la distancia mínima. Es decir, a cada punto interior se le asigna un valor que viene dado por la distancia mínima a
. Se forma así lo que se llama una segmentación (se divide la silueta en partes) que no es muy regular (he apostado con David a que vosotros, los lectores, podéis encontrar un ejemplo muy rápido…). Para utilizar esta manera de relacionar puntos del interior con la frontera lo que se hace es resolver la ecuación eikonal con condiciones de borde Dirichlet sobre la silueta: es decir se resuelve
. Esta manera tiene ciertas desventajas, algunas matemáticamente obvias. Por ejemplo podemos convencernos rápidamente de que la ecuación anterior no tiene una única solución. En efecto, consideremos el problema en una dimensión: tenemos así a ecuación diferencial ordinaria
en un intervalo acotado. Podemos construir infinitas soluciones, basta con ir construyendo triángulos con lados de pendiente 1 o -1. Podemos construirlos más grandes, más pequeños, unos pocos o muchos… Cada una de estas construcciones será una solución ‘débil’ (otro día hablaremos más de la soluciones débiles, hoy lo dejo caer sólo :P).
Así que si descartamos la aproximación anterior tenemos que proponer una nueva… para que no nos digan que hacemos críticas destructivas. Así que lo que hacemos (ver la referencia más abajo) es considerar un camino aleatorio, y más concretamente consideramos el tiempo medio, que denotamos por que tarda una partícula que siga dicho camino aleatorio en golpear
si inicialmente estaba en un punto
. Cuando a cada
le asignamos este
tenemos una segmentación. ¿Qué ecuación diferencial cumple? En (1) la motivan razonando de la siguiente manera: sea
el tiempo medio que emplean estas partículas en golpear el contorno del dominio saliendo desde el punto
(interno de la silueta
). Entonces si
se tiene que
, si no, por ser las probabilidades uniformes se tiene que se puede calcular conociendo los valores de los puntos vecinos. Efectivamente, si estamos en un punto
y conocemos el valor de
en los puntos inmediatamente vecinos lo que podemos hacer es ‘gastar un movimiento’ en movernos a un punto vecino (siguiendo el camino aleatorio uniforme, lo que nos da una probabilidad 1/4 de elegir un determinado punto adyacente) y sumarle el tiempo medio que se emplea desde este nuevo punto. Por lo tanto se tiene que el valor es
Entonces observamos que la discretización del Laplaciano es
y por lo tanto la ecuación anterior es una versión discretizada de
Una manera rigurosa de obtener la misma conclusión es considerar la ecuación
con datos de borde Dirichlet homogéneos. Sea ahora
. Entonces se tiene
La idea de la demostración es aplicar la fórmula de It\^ o (ver (2) o (3)) al proceso $u(X_s)$, donde $X_s$ es un movimiento browniano, obteniendo la fórmula siguiente tras tomar esperanzas
Ahora usamos las condiciones de borde y la ecuación para obtener
concluyendo la demostración.
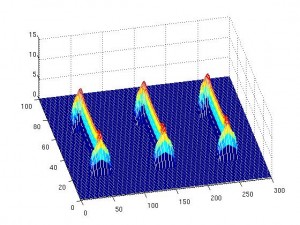
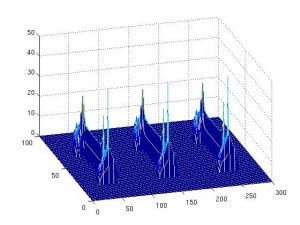
Una vez que tenemos solución de la ecuación de Poisson anterior lo que hacemos es definir nuevas funciones
y y
(entre otras). La función
tiene ciertas propiedades que la hacen interesantes, pero para el tratamiento de imágenes lo más importante es que los valores altos de
indican concavidades (allí el gradiente es grande) y que podemos utilizar el método del umbral para dividir nuestra forma en partes sin perder información. La función
(cuyo operador es el 1-Laplaciano) tiene la propiedad de que ciertos valores se alcanzan en zonas curvadas. Por lo tanto sirve para encontrar esquinas en nuestra forma. Los valores negativos de
indican concavidades. Cuanto más negativo más ‘picuda’ es la concavidad. Al reves también funciona, los valores altos indican convexidades. Así extraemos información de la imagen y el ordenador puede discernir entre ellas.
Para el lector familiarizado con Matlab dejamos un código. Con estas funciones se puede experimentar un poquito lo que hemos estado diciendo.
function [img,img2,u,t,cnt]=imagessor(tol,itmax,image)
%this program use the sor method for solve the poisson equation in a silhouette
%tol is the tolerance
%itmax is the maximum number of iterations
%image is an png image.
%Rafael Granero Belinchontic
img=imread(image);
figure;imagesc(img);
input(‘Press any key’)
img=double(img);
[H,W]=size(img);
w= 2 / ( 1 + sin(pi/(H+1)) );%our overrelaxation parameter
for i=1:H
for j=1:W
img2(i,j)=abs(img(i,j)-255); %change white for black and viceversa
end
end
img2;
figure; imagesc(img2);
input(‘Press any key’)
clear i,j;
%now we start with the algorithm. Like maybe it will be difficult put the geometry of the silhouette
%we use the easy bounday conditions to treat all the image, but we only solve the poisson inside the silhouette.
%This maybe is not efficiently, but is easier.
u=img2;
v=u;
err=1;
cnt=0;
while((err>tol)&(cnt<=itmax))
for i=2:H-1
for j=2:W-1
if (img2(i,j)==0)else
v(i,j)=u(i,j)+w*(v(i-1,j) + u(i+1,j) + v(i,j-1) + u(i,j+1) +1 – 4*u(i,j))/4;
E(i,j)=v(i,j)-u(i,j);
end
end
end
err=norm(E,inf);
cnt=cnt+1;
u=v;
end
u=flipud(u);
figure;imagesc(u);
mesh(u)
t=toc;function [Phi,t]=phi(u,NGu)
%This program calculate the function phi=u+NGu^2
%NGu is the norm of the gradient of u
%Rafael Granero Belinchontic
[H,W]=size(NGu);
for i=1:H
for j=1:W
Phi(i,j)=u(i,j)+NGu(i,j)^2;
end
end
t=toc;function [Psi,t]=psiimages(u,Gux,Guy,NGu)
%This program calculate the function psi=-div(gradient(u)/norm(gradient(u))
%NGu is the norm of the gradient of u
%Gux is the first component of the gradient,
%Guy is the second one
%Rafael Granero Belinchontic
[H,W]=size(NGu);
for i=2:H
for j=2:W
Psix(i,j)=((Gux(i,j)-Gux(i-1,j))*NGu(i,j)-Gux(i,j)*(NGu(i,j)-NGu(i-1,j)))/NGu(i,j)^2;
Psiy(i,j)=((Guy(i,j)-Guy(i,j-1))*NGu(i,j)-Guy(i,j)*(NGu(i,j)-NGu(i,j-1)))/NGu(i,j)^2;
Psi(i,j)=-Psix(i,j)-Psiy(i,j);
end
end
t=toc;function [Gux,Guy,NGu,t]=gradient(u)
%This program calculate the gradient and its norm
%Gux is the first component of the gradient,
%Guy is the second one
%NGu is the norm of the gradient
%Rafael Granero Belinchontic
[H,W]=size(u);
for i=2:H
for j=2:W
Gux(i,j)=u(i,j)-u(i-1,j);
Guy(i,j)=u(i,j)-u(i,j-1);
NGu(i,j)=(Gux(i,j)^2+Guy(i,j)^2)^0.5;
end
end
t=toc;
(1) L.Gorelick, M.Galun, E.Sharon, R.Basri, A.Brandt, ‘Shape Representation and Classification Using the Poisson Equation’, IEEE transaction on pattern analysis and machine intelligence, 28 (2006), no.12, 1991-2004.
(2) H.Kunita, Stochastic differential equation and stochastic flows of diffeomorphism, Lecture Notes in Math. vol 1097, Springer, 1984.
(3) H.Kunita, Stochastic flows and stochastic differential equations, Cambridge studies in advanced mathematics, 1997.