Category Archives: Aplicaciones
Resolviendo la ecuación de ondas…
De cuerdas y tambores, o cómo la física aparece en un problema de matemáticas
A Francisco Gancedo le conceden el premio “Real Maestranza de Caballería de Sevilla”
¿Cómo empezar bien el año? Pues recibiendo un premio. Esa ha sido la manera de comenzar el 2012 de Francisco Gancedo ya que la Real Academia Sevillana de Ciencias le ha concedido el premio “Real Maestranza de Caballería de Sevilla” por sus investigaciones en el estudio de problemas de frontera libre asociados a interfases entre fluidos incompresibles. O de otra manera: olas en diversas situaciones (puede leerse una entrada sobre el tema aquí).
¡Felicidades Paco!
Usando las Matemáticas en biología
Diego Córdoba es el nuevo Premio “Miguel Catalán”
El otro día, el Martes pasado concretamente, se anunciaron los Premios “Miguel Catalán”. Estos premios los da la Comunidad de Madrid al investigador más sobresaliente de todas las ciencias y tenemos el gusto de anunciar que el Premio en la categoría Jóven se lo ha llevado Diego Córdoba Gazolaz por sus trabajos en Mecánica de Fluidos. Algunos de los resultados en los que ha participado ya han sido anunciados aquí.
Nuestra más sincera enhorabuena desde aquí.
Las paradojas del C.S.I.
En esta nueva entrada de la serie de las Paradojas (ver las otras entradas aquí ,
aquí y aquí) vamos a tratar de explicar paradojas que nacen de la mala interpretación de la probabilidad.
Todo el mundo conoce la serie C.S.I. y sus secuelas. En la serie un grupo de investigadores de la policía se dedican a buscar pruebas para resolver casos que sin el uso de avanzadas técnicas científicas y la participación de estos peritos forenses sería imposible solucionar. Los capítulos de la serie cuentan el asesinato y cómo los miembros del C.S.I. han recabado las pistas y acaban con la detención del culpable. Sin embargo hay una última parte que nunca tratan. Me refiero al juicio. Y es que, aunque tal cual está en la serie parece obvia la culpabilidad dadas las pruebas que se han encontrado, la valoración de las evidencias es un tema peliagudo en extremo.
El problema si lo escribimos de manera matemática involucra probabilidades condicionadas. La definición de este objeto (sacada de la wikipedia) es, dado un espacio de probabilidad y dos eventos o sucesos
con
, la probabilidad condicional de ‘A’ dado ‘B’ está definida como:
Hemos de pensar en B como en que ha ocurrido algo que modifica la información que tenemos disponible.
Así, si dado un caso de los de la serie de televisión, consideramos los sucesos
1) “se encuentran evidencias”. Este suceso se escribe E
2) “el sospechoso es culpable”. Este suceso se escribe C.
3) “el sospechoso es inocente”. Este suceso se escribe I.
4) “el sospechoso es inocente dado que hemos encontrado la prueba E”. Este suceso lo escribimos como .
y
5) “el sospechoso es culpable dado que hemos encontrado la prueba E”. Este suceso lo denotamos por .
Así la probabilidad que le interesa al juez con sobrecarga de trabajo que le toque es o bien
.
Vamos a motivar nuestra nueva entrada sobre paradojas con un caso famosísimo en su época: el caso Dreyfus (ver esta página para más detalles). Esta novela por entregas tiene de todo, un bueno inocentón, el propio Dreyfus, un malo malísimo con multitud de problemas, Esterházy, y hasta cameos de personajes famosos como por ejemplo Zola. Un brevísimo resumen: tras la guerra franco-prusiana del siglo XIX se detectó una filtración en el ejército francés. Se detuvo al Capitán Alfred Dreyfus. Se tenía como principal evidencia una carta. Lo que ocurrió es que un “perito” estimó la probabilidad de coincidencia entre la letra de la carta y la letra del Capitán Dreyfus, suponiendo que Dreyfus fuese inocente, como 0.2. Como este mismo perito había observado 4 coincidencias y éstas se asumían independientes (es decir, que la probabilidad de las cuatro es el producto de las cuatro probabilidades) el perito conluyó que Dreyfus era culpable porque, según él, “la probabilidad de que fuese inocente dada la evidencia (las coincidencias entre la carta y la letra de Dreyfus) es muy pequeña”. El lector avispado se habrá dado cuenta del truco. El perito “estima” (que esa es otra cosa, ¿por qué la probabilidad es 0.2?) y entonces concluye que
.
Veamos qué implicaciones tiene la asunción . Se tiene que
y, similarmente,
Ahora consideramos la cantidad
Si ahora usamos la hipotesis de que y
se concluye que
lo que contradice la presunción de inocencia en casi todos los casos.
¿Cuál es la moraleja? Pues que la probabilidad no es intuitiva nunca (o casi nunca) y que todos los argumentos probabilísticos deben ser cuidadosamente repasados. Si no lo hacemos así nos arriesgamos a repetir tristes historias (ver esta entrada de la wikipedia o esta otra).
–Referencias: 1) Estadística y Evaluación de la Evidencia para Expertos Forenses. Segunda Edición. C. Aitken y F. Taroni. (Traducido por: J. Lucena, L. Gil y R. Granero), Ed. Dykinson.
— Con esta entrada participamos en la edición 2.7 del Carnaval de Matemáticas, que está organizado por La Aventura de la Ciencia.
Las olas: Un matemático en la playa.
Ya va haciendo calor y empieza a apetecer el irse a la piscina o a la playa. Sin duda la playa es uno de los sitios menos entendidos por el mundo científico y más visitados por el resto del mundo. El fenómeno al que me refiero cuando digo que no se comprende completamente, claro está, son las olas. En esta entrada estudiaremos diversos casos de olas entre fluidos ilustrando el texto con diversos videos.
[iframe: width=”400″ height=”320″ src=”http://www.youtube.com/embed/GEl-Qu7ApGQ” frameborder=”0″ allowfullscreen]Vamos a empezar hablando de un caso un poco más general que las típicas olas en la superficie del mar. En matemáticas entendemos por interfase entre fluidos a la parte donde estos entran en contacto entre sí. Así una ola es la interfase entre el aire y el agua. Una interfase entre fluidos con distintas propiedades puede exhibir un comportamiento muy complicado, patológico si se quiere, pero que es, pienso yo al menos, visualmente muy bonito. Estoy pensando por ejemplo en singularidades como pueden ser las llamadas singularidades de Kelvin-Helmholtz o Rayleigh-Taylor. Hagamos una parada antes de proseguir con nuestras olas.
Supongamos por un momento que tenemos dos fluidos con densidades distintas, por fijar ideas digamos aceite y agua, de manera que el fluido más denso (el agua) está en el fondo de un recipiente cerrado completamente (un tubo con ambos extremos taponados). El fluido menos denso (el aceite) reposa encima del agua. Supongamos ahora que dicho tubo, y por tanto los fluidos, está en reposo, por ejemplo en una mesa. La pregunta es ¿qué ocurre si, repentinamente, inclinamos dicho recipiente? Veamos unos vídeos con este experimento:
[iframe: width=”400″ height=”320″ src=”http://www.youtube.com/embed/CL7s8h7mtPE” frameborder=”0″ allowfullscreen] [iframe: width=”400″ height=”320″ src=”http://www.youtube.com/embed/ggEp4n6Bhps” frameborder=”0″ allowfullscreen] [iframe: width=”400″ height=”320″ src=”http://www.youtube.com/embed/1XqJJfw63zQ” frameborder=”0″ allowfullscreen]Lo que vemos en el video es que la interfase “se enrolla” sobre sí misma. Esto es debido a que las velocidades (que son un vector en 3D) tangentes a la interfase tienen signo distinto. Es decir, si lo pensamos en una interfase en 2D (una curva) sería que la velocidad en el fluido que está encima de la interfase “señala hacia la izquierda” mientras que para el fluido que está debajo de la interfase “señala a la derecha”. De ahí esa tendencia a girar y enrollarse.
Supongamos ahora que cambiamos el orden de los fluidos. Ahora tenemos (por ejemplo porque tenemos una barrera entre ambos fluidos) el agua reposando sobre el aceite. ¿Qué ocurre si retiramos rápidamente la barrera entre ambos fluidos? Bueno, pues que el fluido más denso, por la gravedad, caerá hacía abajo, empujando en su camino al fluido menos denso, que subirá hacía arriba. Vale, el caso es que lo que va a ocurrir es sencillo de vaticinar, lo curioso aquí es la manera en que ocurre. Vayamos otro rato a youtube…
[iframe: width=”400″ height=”320″ src=”http://www.youtube.com/embed/VlAzyVx7N9M” frameborder=”0″ allowfullscreen] [iframe: width=”400″ height=”320″ src=”http://www.youtube.com/embed/8EkFL-8wIUI” frameborder=”0″ allowfullscreen]Tras ver estos experimentos y haber pensado un poquito nos damos cuenta de que el que quiera entender bien estos procesos tiene mucho trabajo por delante. Y ahí estamos bregando algunos…
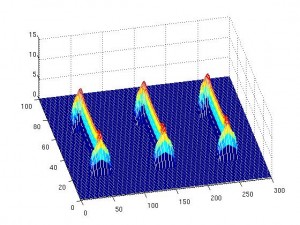
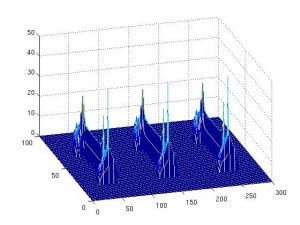
Volvamos a las olas. Hace tan sólo unos días uno de mis jefes (Diego Córdoba) y algunos de mis compañeros (Ángel Castro, Francisco Gancedo y Javier Gómez) y otros colaboradores (el medallista Field Charles Fefferman) hicieron un importante avance. Probaron la existencia de otro tipo de singularidad para el caso de las olas. Bautizaron a esta singularidad como “splash”. Arremanguémonos y veamos un poco las matemáticas que hay debajo de todo esto…
Consideremos una curva en el plano. Esta será nuestra ola inicial. La evolucion de esta ola viene dada por la evolución del fluido bajo ella. Se trata así de un problema de frontera libre, es decir, donde el propio dominio es una incógnita. Así tenemos que, bajo la ola, se verifican las ecuaciones de Euler incompresibles y que además el fluido es irrotacional. Sobre la curva suponemos que tenemos el vacío (esto es un buen modelo porque el agua tiene una densidad mucho mayor a la del aire). Lo que se sabía antes de los trabajos de Diego y compañía eran la existencia local de solución, es decir, que una ola “suave” sigue siendo una ola “suave” al menos un corto tiempo. Esta existencia local es cierta tanto en el caso donde se supone que la profundidad del mar es infinita como en el caso con un lecho marino predeterminado (son resultados de S. Wu y D. Lannes, respectivamente). También se sabe que si las olas “son muy planitas” la existencia es global, es decir, la ola existe para cualquier tiempo (resultados obtenidos independientemente por S. Wu y P. Germain, N. Masmoudi y J. Shatah).
[iframe: width=”400″ height=”320″ src=”http://www.youtube.com/embed/SdPI6yrjJoM” frameborder=”0″ allowfullscreen]Los resultados con bandera española en este tema comienzan con un artículo (de A. Castro, D. Córdoba, C. Fefferman, F. Gancedo y M. López) donde se prueba que una ola que empieza siendo un grafo, es decir, se puede escribir como , deja en un tiempo finito
de ser un grafo. De otra manera, la ola rompe. Matemáticamente esto es que la derivada espacial de la ola se hace infinita en algún punto. El resultado de hace unos días que he mencionado más arriba abunda más en esta línea. Lo que A. Castro, D. Córdoba, C. Fefferman, F. Gancedo y J. Gómez prueban es que existen olas que empiezan siendo curvas suaves y que en un tiempo finito se tocan. Es decir, se ha perdido la propiedad de ser una curva sin autointersecciones. Así es plausible el escenario de comenzar con un grafo, evolucionar hasta perder la propiedad de ser un grafo, es decir, la ola rompe, y, al continuar pasando el tiempo, la curva se acabe autointersecando. Esto es justamente lo que hemos visto en el primer video de esta entrada. Así que podemos concluir dos cosas: una es que algo tan cotidiando como una ola puede ser matemáticamente un problema muy difícil. La segunda cosa que podemos aprender es que nuestro modelo para la dinámica de fluidos funciona en el sentido de que recupera comportamientos reales observados en la naturaleza.
Antes de acabar quiero agradecer a mi compañero Javier Gómez que nos haya dejado el video de sus simulaciones.
—-Esta es nuestra contribución a la edición 2.5 del Carnaval de Matemáticas (http://carnavaldematematicas.bligoo.es/), que está siendo albergado por el blog Juegos Topológicos (http://topologia.wordpress.com/d).
Caminos aleatorios e imágenes
Esta es nuestra entrada para el Carnaval de Matemáticas 2.2 (alojado esta vez en Gaussianos).
Muchas veces se ha escrito sobre la relación entre los caminos aleatorios y la ecuación del calor, y quizá próximamente tratemos nosotros ese tema. Sin embargo hoy vamos a ver una aplicación poco conocida de esa relación. En esta entrada vamos a tratar brevemente una manera de emplear las matemáticas, y mas concretamente los caminos aleatorios o las trayectorias brownianas, para que un ordenador sepa qué imagen está ‘viendo’. Ahora que han puesto unos radares de tramo (que funcionan memorizando las matrículas de los coches y midiendo tiempos para calcular la velocidad media del tramo donde está el radar) en las carreteras españolas este problema tiene una clara aplicación práctica.
Desde hace unos años el tratamiento de imágenes usando ecuaciones en derivadas parciales es un área de investigación matemática floreciente. Normalmente tratan el problema de detectar los contornos de una imagen o de suavizarlos (de manera que veamos mejor la imagen). Nuestro problema es ligeramente distinto. Nosotros, dada una silueta (es decir un contorno cerrado y suave que encierra un área negra mientras que lo de fuera es blanco), tenemos que enseñar al ordenador a sacar propiedades de los contornos de manera que aprenda a distinguir entre las distintas siluetas.
La manera usual de extraer propiedades de una silueta es ‘medir’ y ‘clasificar’ los puntos del interior del contorno en función de su posición relativa a la curva que delimita la silueta (a partir de ahora la denotaremos S, mientras que el contorno será ). Esto puede hacerse por ejemplo con la distancia mínima. Es decir, a cada punto interior se le asigna un valor que viene dado por la distancia mínima a
. Se forma así lo que se llama una segmentación (se divide la silueta en partes) que no es muy regular (he apostado con David a que vosotros, los lectores, podéis encontrar un ejemplo muy rápido…). Para utilizar esta manera de relacionar puntos del interior con la frontera lo que se hace es resolver la ecuación eikonal con condiciones de borde Dirichlet sobre la silueta: es decir se resuelve
. Esta manera tiene ciertas desventajas, algunas matemáticamente obvias. Por ejemplo podemos convencernos rápidamente de que la ecuación anterior no tiene una única solución. En efecto, consideremos el problema en una dimensión: tenemos así a ecuación diferencial ordinaria
en un intervalo acotado. Podemos construir infinitas soluciones, basta con ir construyendo triángulos con lados de pendiente 1 o -1. Podemos construirlos más grandes, más pequeños, unos pocos o muchos… Cada una de estas construcciones será una solución ‘débil’ (otro día hablaremos más de la soluciones débiles, hoy lo dejo caer sólo :P).
Así que si descartamos la aproximación anterior tenemos que proponer una nueva… para que no nos digan que hacemos críticas destructivas. Así que lo que hacemos (ver la referencia más abajo) es considerar un camino aleatorio, y más concretamente consideramos el tiempo medio, que denotamos por que tarda una partícula que siga dicho camino aleatorio en golpear
si inicialmente estaba en un punto
. Cuando a cada
le asignamos este
tenemos una segmentación. ¿Qué ecuación diferencial cumple? En (1) la motivan razonando de la siguiente manera: sea
el tiempo medio que emplean estas partículas en golpear el contorno del dominio saliendo desde el punto
(interno de la silueta
). Entonces si
se tiene que
, si no, por ser las probabilidades uniformes se tiene que se puede calcular conociendo los valores de los puntos vecinos. Efectivamente, si estamos en un punto
y conocemos el valor de
en los puntos inmediatamente vecinos lo que podemos hacer es ‘gastar un movimiento’ en movernos a un punto vecino (siguiendo el camino aleatorio uniforme, lo que nos da una probabilidad 1/4 de elegir un determinado punto adyacente) y sumarle el tiempo medio que se emplea desde este nuevo punto. Por lo tanto se tiene que el valor es
Entonces observamos que la discretización del Laplaciano es
y por lo tanto la ecuación anterior es una versión discretizada de
Una manera rigurosa de obtener la misma conclusión es considerar la ecuación
con datos de borde Dirichlet homogéneos. Sea ahora
. Entonces se tiene
La idea de la demostración es aplicar la fórmula de It\^ o (ver (2) o (3)) al proceso $u(X_s)$, donde $X_s$ es un movimiento browniano, obteniendo la fórmula siguiente tras tomar esperanzas
Ahora usamos las condiciones de borde y la ecuación para obtener
concluyendo la demostración.
Una vez que tenemos solución de la ecuación de Poisson anterior lo que hacemos es definir nuevas funciones
y y
(entre otras). La función
tiene ciertas propiedades que la hacen interesantes, pero para el tratamiento de imágenes lo más importante es que los valores altos de
indican concavidades (allí el gradiente es grande) y que podemos utilizar el método del umbral para dividir nuestra forma en partes sin perder información. La función
(cuyo operador es el 1-Laplaciano) tiene la propiedad de que ciertos valores se alcanzan en zonas curvadas. Por lo tanto sirve para encontrar esquinas en nuestra forma. Los valores negativos de
indican concavidades. Cuanto más negativo más ‘picuda’ es la concavidad. Al reves también funciona, los valores altos indican convexidades. Así extraemos información de la imagen y el ordenador puede discernir entre ellas.
Para el lector familiarizado con Matlab dejamos un código. Con estas funciones se puede experimentar un poquito lo que hemos estado diciendo.
function [img,img2,u,t,cnt]=imagessor(tol,itmax,image)
%this program use the sor method for solve the poisson equation in a silhouette
%tol is the tolerance
%itmax is the maximum number of iterations
%image is an png image.
%Rafael Granero Belinchontic
img=imread(image);
figure;imagesc(img);
input(‘Press any key’)
img=double(img);
[H,W]=size(img);
w= 2 / ( 1 + sin(pi/(H+1)) );%our overrelaxation parameter
for i=1:H
for j=1:W
img2(i,j)=abs(img(i,j)-255); %change white for black and viceversa
end
end
img2;
figure; imagesc(img2);
input(‘Press any key’)
clear i,j;
%now we start with the algorithm. Like maybe it will be difficult put the geometry of the silhouette
%we use the easy bounday conditions to treat all the image, but we only solve the poisson inside the silhouette.
%This maybe is not efficiently, but is easier.
u=img2;
v=u;
err=1;
cnt=0;
while((err>tol)&(cnt<=itmax))
for i=2:H-1
for j=2:W-1
if (img2(i,j)==0)else
v(i,j)=u(i,j)+w*(v(i-1,j) + u(i+1,j) + v(i,j-1) + u(i,j+1) +1 – 4*u(i,j))/4;
E(i,j)=v(i,j)-u(i,j);
end
end
end
err=norm(E,inf);
cnt=cnt+1;
u=v;
end
u=flipud(u);
figure;imagesc(u);
mesh(u)
t=toc;function [Phi,t]=phi(u,NGu)
%This program calculate the function phi=u+NGu^2
%NGu is the norm of the gradient of u
%Rafael Granero Belinchontic
[H,W]=size(NGu);
for i=1:H
for j=1:W
Phi(i,j)=u(i,j)+NGu(i,j)^2;
end
end
t=toc;function [Psi,t]=psiimages(u,Gux,Guy,NGu)
%This program calculate the function psi=-div(gradient(u)/norm(gradient(u))
%NGu is the norm of the gradient of u
%Gux is the first component of the gradient,
%Guy is the second one
%Rafael Granero Belinchontic
[H,W]=size(NGu);
for i=2:H
for j=2:W
Psix(i,j)=((Gux(i,j)-Gux(i-1,j))*NGu(i,j)-Gux(i,j)*(NGu(i,j)-NGu(i-1,j)))/NGu(i,j)^2;
Psiy(i,j)=((Guy(i,j)-Guy(i,j-1))*NGu(i,j)-Guy(i,j)*(NGu(i,j)-NGu(i,j-1)))/NGu(i,j)^2;
Psi(i,j)=-Psix(i,j)-Psiy(i,j);
end
end
t=toc;function [Gux,Guy,NGu,t]=gradient(u)
%This program calculate the gradient and its norm
%Gux is the first component of the gradient,
%Guy is the second one
%NGu is the norm of the gradient
%Rafael Granero Belinchontic
[H,W]=size(u);
for i=2:H
for j=2:W
Gux(i,j)=u(i,j)-u(i-1,j);
Guy(i,j)=u(i,j)-u(i,j-1);
NGu(i,j)=(Gux(i,j)^2+Guy(i,j)^2)^0.5;
end
end
t=toc;
(1) L.Gorelick, M.Galun, E.Sharon, R.Basri, A.Brandt, ‘Shape Representation and Classification Using the Poisson Equation’, IEEE transaction on pattern analysis and machine intelligence, 28 (2006), no.12, 1991-2004.
(2) H.Kunita, Stochastic differential equation and stochastic flows of diffeomorphism, Lecture Notes in Math. vol 1097, Springer, 1984.
(3) H.Kunita, Stochastic flows and stochastic differential equations, Cambridge studies in advanced mathematics, 1997.
¿Podemos ir hacia atrás (matemáticamente) en el tiempo?
Me comentó David que sería interesante que explicase un poquito de lo que significa la reversibilidad temporal desde el punto de vista de las ecuaciones en derivadas parciales (EDPs de ahora en adelante). Es decir, sin mencionar nada de entropías. Este es un tema muy interesante e importante aunque a primera vista parezca una tontería. Lo hemos puesto como una serie de dos entradas. La primera (esta que estás leyendo) presentará las EDPs más fáciles y estudiará sus propiedades de cara a la reversibilidad temporal. En la segunda veremos la derivación de unos modelos más complicados y trataremos de entender dónde aparece la irreversibilidad temporal. Lo cierto es que en cierto modo es llamativo, pues las leyes de Newton son reversibles en tiempo y muchas (casi todas) de las ecuaciones de las que hablaremos surgen de ellas.
Viendo qué ocurre:
Para entender qué quiere decir y qué implica la reversibilidad (o irreversibilidad) temporal hemos de comprender primero los ejemplos más básicos de EDPs. Como dato para los técnicos supondré que todos los problemas están puestos para . Inmerso en el texto hay imágenes .jpg, imágenes animadas .gif (pinchad en ellas para que empiecen a moverse) y código Matlab (¡usadlo si podéis!).
La ecuación del transporte:
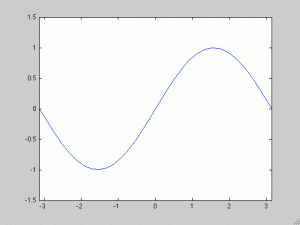
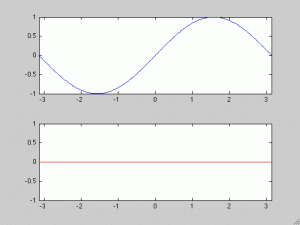
Comenzaremos con la ecuación del transporte unidimensional con coeficientes constantes. Esta es la EDP más sencilla que podemos poner.
Supondremos que es una función derivable con derivada continua una vez. La solución de esta ecuación es
(¡comprobadlo!). Esta ecuación se llama ‘del transporte’ porque lo que hace es eso ‘mueve’ nuestra distribución inicial
. Si queremos cambiar el sentido del tiempo hemos de hacer el cambio
por
. Entonces la nueva ecuación es
Observamos que el cambiar el tiempo de sentido es equivalente a cambiar el signo de . Si utilizamos el código que propongo con varios valores de
observamos que este parámetro es una velocidad. Por lo tanto, parece natural que cambiar el sentido del tiempo cambie el sentido del movimiento. Es decir, que si para
íbamos a la derecha, para tiempos negativos (o equivalentemente
) tenemos que ir a la izquierda. Concluímos así que la ecuación del transporte es reversible en tiempo y que la reversibilidad es muy natural si partimos del proceso físico que se modela con esta ecuación.
Otra consecuencia, ésta mucho más sutil, de la reversibilidad temporal es que nuestra solución NUNCA va a ser mejor que nuestro dato inicial . Esto es obvio en este caso porque tenemos una solución explícita, pero es cierto en general. Si
tuviese más derivadas que
entonces dando la vuelta al tiempo tendríamos una contradicción.
function [u,x,t]=transporte(dx,dt,f,c)
%%
%Funcion que me aproxima la solucion exacta (conocida) de la
%ecuacion del transporte u_t+cu_x=0 con dato inicial
% u(0,x)=f(x), paso espacial dx y paso temporal dt.
%f sera una funcion
% Rafael Granero Belinchon
%%%Definicion de parametros:
T=10; %El tiempo final
t=0:dt:T; %el vector de tiempos
x=-pi:dx:pi; %el vector de espacio donde queremos
%nuestra aproximacion. No necesitamos condiciones de borde ¿por que?
u=zeros(length(x),length(t));
F=feval(f,x);%Calculo de la solucion:
%La solucion del problema anterior es u(x,t)=f(x-ct)
u(:,1)=F;
for j=2:length(t)
u(:,j)=feval(f,x-c*t(j));
plot(x,u(:,j-1));%Representacion de los resultados
drawnow
endfunction f=prueba(x)
f=sin(x);
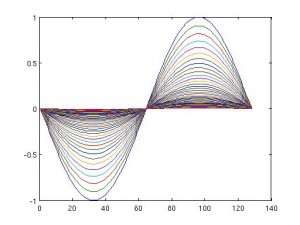
La ecuación de ondas:
La siguiente ecuación es el paradigma de ecuación hiperbólica. Me refiero a la ecuación de ondas. Viendo el nombre está claro qué proceso físico quiere describir ¿no?.
Esta ecuación se escribe
Visualmente parece mucho más complicada que la ecuación del transporte… sin embargo en realidad es igual (al menos en un cierto sentido). Vamos a escribirla como un sistema. Para ello definimos el sistema
Si ahora derivamos en tiempo la ecuación para y utilizamos la segunda ecuación obtenemos
Es decir, que la ecuación de ondas no es más que dos transportes acoplados. Sin embargo todavía podemos hacerlo mejor. Podemos darnos cuenta de que el operador diferencial se puede escribir como
y por lo tanto si tenemos con
tenemos una solución de la ecuación original. Concluímos que, como la ecuación del transporte era reversible, la ecuación de ondas, que se puede escribir como un par de ecuaciones del transporte debe ser reversible también.
La ecuación del calor:
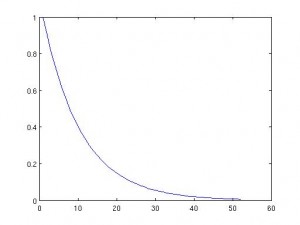
Esta ecuación es parabólica. Se escribe
Visualmente parece estar a medio camino entre la ecuación del transporte y la ecuación de ondas, sin embargo su comportamiento en radicalmente distinto. Para convencernos de ello podemos ‘jugar’ un poco con el código Matlab que adjunto. Los datos iniciales por defecto son los mismos, pero os animo a cambiarlos.
function [u,x,t,mx]=heatff(N,dt,K)
%%
%Funcion que me aproxima la solucion de la
%ecuacion del calor con dato inicial seno
%con condiciones periodicas (para usar FFT)
%N es el numero de nodos espaciales que se quieren
%usar. dt es el paso temporal que se quiere.
%K es la constante de difusion.
%Devuelve el espacio, el tiempo, la aproximacion de
%la solucion y el maximo de dicha solucion en cada tiempo
%Rafael Granero Belinchon
%%
T=5;%Tiempo final
dx=2*pi/(N-1);
x=-pi:dx:pi;%Espacio
t=0:dt:T;%Tiempo
uo=sin(x);%dato inicial
for k=1:N/2 %Operador laplaciano en espacio de fourier
L(k)=(k-1)*(k-1);
L(k+N/2)=(N/2-k+1)*(N/2-k+1);
end
L=K*L;
u(:,1)=uo’;
mx(1)=max(uo);
for l=1:length(t)
u(:,l+1)=ifft(exp(-L*dt*l).*fft(uo))’;%solucion
mx(l+1)=max(u(:,l+1));%Evolucion del maximo
plot(x,u(:,l));axis([-pi,pi,-1,1]);%Representacion de los resultados
drawnow
end
end
Para estudiar esta ecuación vamos a utilizar la transformada de Fourier. Para la transformada de Fourier de usaremos la notación
. Así si transformamos la ecuación en espacio obtenemos las ecuaciones diferenciales ordinarias (EDOs a partir de ahora) indexadas en la longitud de onda
siguientes
Esta ecuación la podemos resolver explícitamente
Observemos ahora qué quiere decir el cambio del sentido del tiempo. De nuevo hagamos el cambio por
. La ecuación nos queda
No se ve nada claro, sin embargo, si buscamos los efectos del cambio en la solución explícita tenemos
de manera que cuando invirtamos la transformada de Fourier estamos calculando una convolución con una función que no está acotada, ni tiene ninguna potencia integrable… Vamos, que nuestra solución (que existe explícitamente) no está en ningún espacio razonable ni con propiedades físicas razonables. Por ejemplo, si es la temperatura, entonces su integral (que es el calor) debe ser finita. Pues si damos la vuelta al tiempo obtenemos calor infinito para cualquier tiempo. Concluímos que la ecuación del calor NO es reversible en tiempo.
Una propiedad que a veces se da en las ecuaciones irreversibles y que es bien interesante es el ‘efecto regularizante’. Es decir, tu dato inicial es continuo (por ejemplo), pero tu solución
es infinitamente derivable para todo tiempo (positivo). Como ya hemos mencionado antes, este comportamiento difiere del de las ecuaciones hiperbólicas usuales. La prueba de esto se puede hacer sin más que multiplicar por
e integrar por partes en espacio (¡comprobadlo!). Después basta observar que la ecuación es invariante por derivación tanto en tiempo como en espacio (¡Concluid el argumento!).
Vistos estos 3 ejemplos parece que hay una relación entre la ‘simetría’ del problema y su reversibilidad temporal. Quiero decir que, al menos de momento, las ecuaciones que tienen el mismo número de derivadas temporales que espaciales han resultado ser reversibles, mientras que las que no las tienen son irreversibles.
Otra cosa que se nos puede ocurrir es que las ecuaciones reversibles sean las que ‘no tiendan a nada’. Así vemos que la ecuación del calor tiende a ser idénticamente cero (necesita tiempo infinto para llegar a serlo) mientras que la ecuación del transporte sólo se movía por el espacio.
Veamos otro ejemplo:
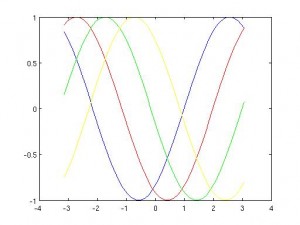
La ecuación de Schrödinger:
Esta ecuación, clave en mecánica cuántica, se escribe
Si repetimos el análisis que hicimos para la ecuación del calor obtenemos que la solución es
que tiene un comportamiento oscilatorio. Por lo tanto, pese a tener una derivada en tiempo y dos en espacio se parece más a una ecuación de ondas que a una ecuación del calor. Observamos que el hecho de que aparezca la unidad imaginaria hace que no sea real, sino compleja. Por lo tanto tiene una función conjugada. Si ahora cambiamos el sentido del tiempo observamos que para la función conjugada
la ecuación es la misma. Por lo tanto si
es nuestra solución con el tiempo hacia delante,
es una solución con el tiempo hacia atrás. Por lo tanto la ecuación de Schrödinger es reversible. Este ejemplo desmonta la hipótesis de que als reversibles debían tener el mismo número de derivadas en espacio y en tiempo.
function [u,x,t,L2,mx]=schrodinger(N,dt)
%%
%Funcion que me aproxima la solucion de la
%ecuacion de schrodinger con dato inicial seno
%con condiciones periodicas (para usar FFT)
%N es el numero de nodos espaciales que se quieren
%usar. dt es el paso temporal que se quiere.
%Devuelve el espacio, el tiempo, la aproximacion de
%la solucion, la norma L^2 de dicha solucion en cada tiempo
%y el maximo de la solucion en todo tiempo.
%Rafael Granero Belinchon
%%
T=5;%Tiempo final
dx=2*pi/(N-1);
x=-pi:dx:pi;%Espacio
t=0:dt:T;%Tiempo
uo=sin(x);%dato inicial
for k=1:N/2 %Operador laplaciano en espacio de fourier
L(k)=(k-1)*(k-1);
L(k+N/2)=(N/2-k+1)*(N/2-k+1);
end
L=i*L;
u(:,1)=uo’;
L2(1)=norm(uo)*dx;
mx(1)=max(abs (uo));
for l=1:length(t)
u(:,l+1)=ifft(exp(-L*dt*l).*fft(uo))’;%solucion
L2(l+1)=norm(u(:,l+1))*dx;%Evolucion de la norma L^2
mx(l+1)=max(abs(u(:,l+1)));%Evolución del máximo
plot(x,real(u(:,l)));axis([-pi,pi,-1,1]);%Representacion de los resultados
drawnow
end
end
Como dato anécdotico de esta ecuación hacemos notar que no puede reflejar efectos relativistas (¿por qué?).
En la próxima entrada, enlazando con esta, trataré la derivación desde la mecánica hamiltoniana de los modelos que se utilizan en mecánica de fluidos y trataré de explicar dónde aparece la irreversibilidad en el proceso. Sin embargo, esto es algo que no está ‘completamente entendido’ todavía.