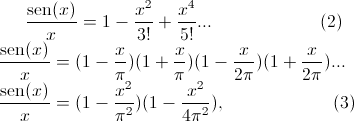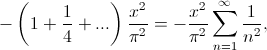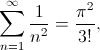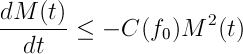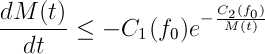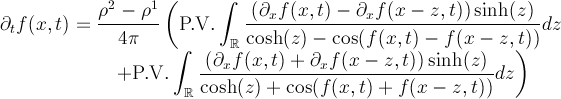Monthly Archives: September 2012

Sobre las singularidades en Euler y la conjetura de Onsager

Posted on by
Reply

Hace algún tiempo escribíamos (ver aquí) sobre un modelo de las ecuaciones de Euler en 3d. La historia de este artículo acabó pronto porque había un error y lo retiraron. Hoy ha aparecido un artículo en Arxiv donde afirman que

A class of singular 3D-velocity vector fields of finite energy is constructed which satisfy the incompressible 3D-Euler equation. It is shown that such a solution scheme does not exist in dimension 2. The solutions constructed are smooth up to finite time where they become singular.

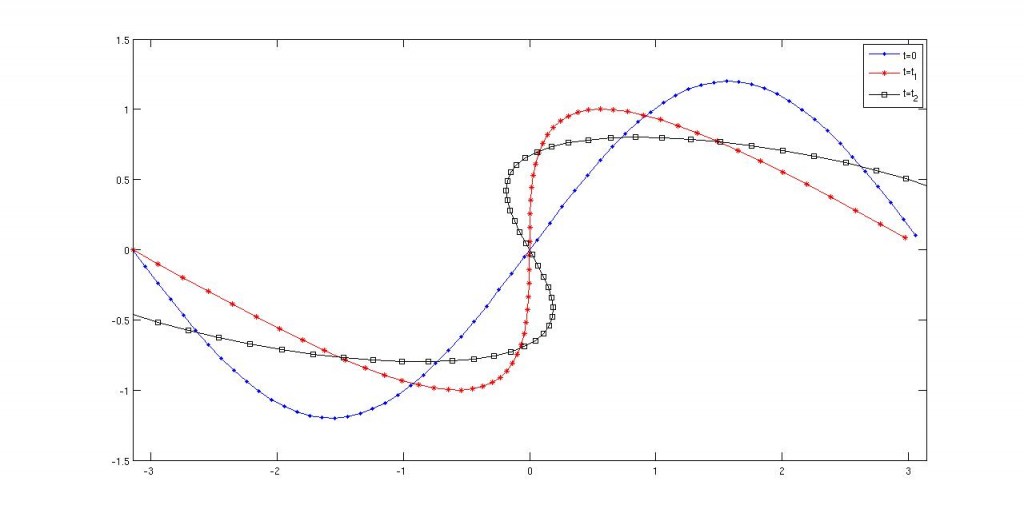
Es decir, afirman haber conseguido soluciones de Euler 3D que son suaves hasta un tiempo finito donde se vuelven singulares. Esto es un teoremazo de ser cierto. Sin embargo, al abrir interesado el artículo empiezan las dudas. El argumento parece ser considerar una familia de soluciones dada por

v_i(x,t)=\frac{f_i(x)}{t-1},

y ver qué han de satisfacer dichas f_i(x) para que v satisfaga las ecuaciones de Euler. Observamos que para esta familia se tiene que

\int_{\mathbb{R}^3}|v(x,t)|^2dx=(t-1)^{-2}\int_{\mathbb{R}^3}|f(x)|^2dx\rightarrow \infty\text{ as }t\rightarrow1. \quad (1)

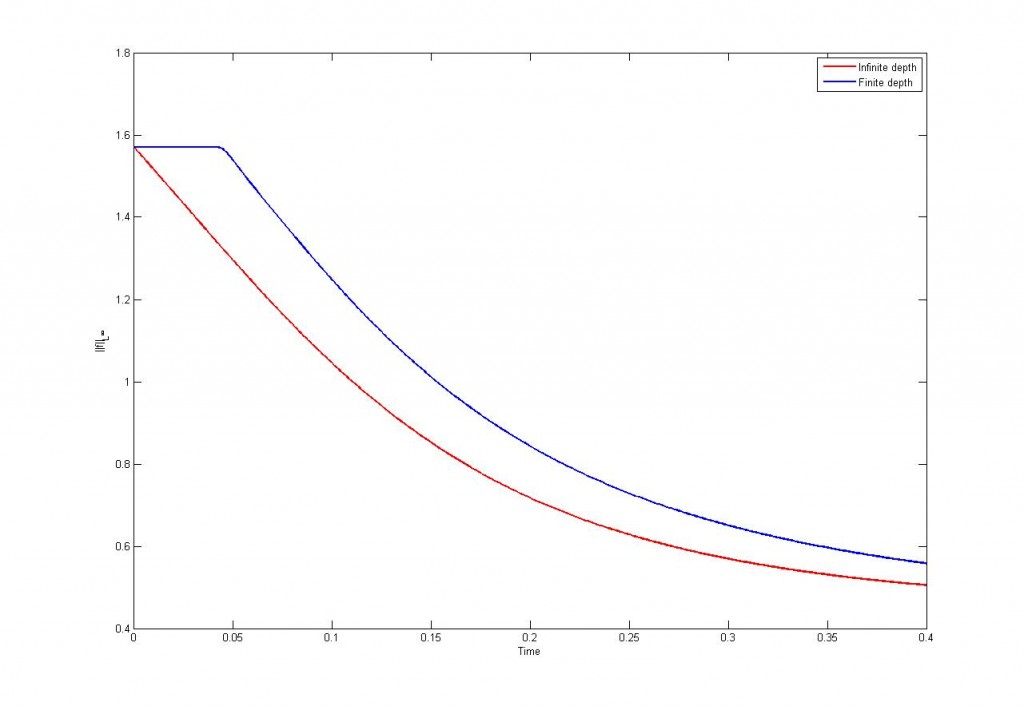
Aquí es donde entra la conjetura de Onsager. Dicha conjetura dice que si v es un campo de velocidades suficientemente regular (más regular que Hölder-1/3) entonces la norma L^2 (que es la cantidad descrita anteriormente en (1)) se conserva. Si no

”…in three dimensions a mechanism for complete dissipation of all kinetic energy, even without the aid of viscosity, is available.” Lars Onsager

Se sabe que si la solución es regular conserva la energía, (es un artículo de Constantin, E y Titi de los años 90) mientras que un reciente artículo de C. De Lellis y L. Székelyhidi Jr. se prueba que existen soluciones Hölder-1/10 que no conservan la energía cinética (ver (1)).

Es decir, o a mí se me está escapando algo o (1) es incompatible con lo que se conoce.

–Nota: Con esta entrada participamos en el Carnaval de Matemáticas en su edición 26, organizado esta vez por ZTFNews.

Euler y el problema de Basilea: Productos infinitos (I)

Posted on by
Reply

El día 18 de Septiembre hizo 229 años de la muerte de Leonhard Euler (ya lo dijimos aquí), así que ¿qué mejor momento para continuar con la serie sobre el problema de Basilea? Ésta serie ya consta de dos entradas (ver aquí y aquí) contando un poco cómo se formula el problema y qué avances se han dado. Vamos a resumirlo un poquito.

El problema de Basilea es calcular la suma de la serie


Jacob Bernoulli fue capaz de probar que la serie efectivamente convergía, i.e. que la suma tiene un valor finito. Una vez que se sabe eso uno puede ir sumando términos a ver qué número va quedando. El problema es que la serie converge muy despacio y hay que sumar muchísimos términos para tener una cantidad aceptable de decimales. Y es aquí donde entra Euler al escribir una serie equivalente que converge mucho más rápido, de manera que hay que sumar menos términos para obtener los mismos decimales.

Veamos qué hizo Euler llegados a este punto. Tenemos que recordar que si tenemos un polinomio

cuyas raíces (reales) son

 entonces podemos escribir 

Con esto en mente observamos que

 tiene cómo raíces 

Así Euler escribe, usando la serie de Taylor,

de donde, si dividimos por x y suponemos que podemos usar la propiedad anterior de los polinomios para una serie de potencias, obtenemos

Ahora basta observar que (3) nos da que el coeficiente que acompaña a x^2 es

y ahora, igualando con (2), obtenemos el resultado

Éste resultado es correcto, pero tiene un enorme “pero”: el argumento es erróneo. No se puede hacer ese desarrollo como producto de las raíces para series. Por ejemplo podemos considerar

que, por tener las mismas raíces que el seno, ¡debería tener el mismo producto infinito! Esta prueba fue muy criticada por la comunidad y Euler siguió trabajando en desarrollos de productos infinitos para el seno de manera que pudiese acallar las quejas con una demostración completamente rigurosa y no sólo con un escueto “pues mi aproximación y el valor exacto que he calculado son iguales…”, pero eso lo dejaremos para otro día…

–Referencias:

Rafael Granero Belinchón, El problema de Basilea: Historia y algunas demostraciones. La Gaceta de la RSME, vol 12, num 4, pag 721-737, 2009.

E. Sandifer, Basel Problem with Integrals, MAA Online, 2004, disponible aquí.

Y aquí un conversor entre fórmulas de Latex e imágenes.

–Nota: Con esta entrada participamos en el Carnaval de Matemáticas en su edición 26, organizado esta vez por ZTFNews.

Problemas de frontera “no-tan-libre” en dinámica de fluidos: las diferencias

Posted on by
Reply

En esta entrada tratamos de presentar de manera sencilla la siguiente pregunta

¿Cómo de importante es el lecho marino para las olas en la superficie?

Así tenemos que estudiar el problema de la evolución de la interfase entre dos fluidos cuando dichos fluidos se encuentran en un medio poroso acotado y, tras hacer unas simulaciones para ver por dónde iban los tiros, dimos los primeros pasos en el estudio matemático del problema. Sin embargo, pese a que en las simulaciones observamos grandes diferencias en los primeros resultados matemáticamente rigurosos no capturamos esos fenómenos.

La primera pregunta que nos hacemos es ¿cuál es la evolución de la amplitud máxima de la ola? Para ellos lo que hacemos es estudiar

Lo que conseguimos probar es

o, lo que es lo mismo, que la amplitud no puede crecer con el tiempo. Este resultado es idéntico al caso donde la profundidad es infinita. Sin embargo en las simulaciones habíamos visto que las diferencias a este nivel eran grandes:

Lo que ocurre es que la velocidad a la que cae la amplitud es distinta. En el caso de profundidad infinita tenemos

donde f_0(x)=f(x,0) es la ola inicial. En el caso de un medio acotado la amplitud evoluciona según

Así hemos obtenido la primera diferencia importante: la interfase en el caso de profundidad finita decae más despacio. 

Ahora cabe preguntarse ¿cómo evoluciona \max_x|\partial_x f(x,t)|? Esta cantidad nos da una idea de cómo es la longitud de onda. Sabemos que en el caso donde el medio no está acotado se tiene que

si \max_x|\partial_x f(x,0)|<1 entonces \max_x|\partial_x f(x,t)|<\max_x|\partial_x f(x,0)|\;\; \forall t>0.

En el caso de que el medio tenga profundidad finita tenemos una condición (razonablemente complicada y que escribiremos F) que involucra no sólo a \max_x|\partial_x f(x,0)| si no también a \max_x|f(x,0)|:

si F(\max_x|\partial_x f(x,0)|,\max_x|f(x,0)|)\leq 0 entonces \max_x|\partial_x f(x,t)|\leq\max_x|\partial_x f(x,0)|\;\; \forall t>0.

Una consecuencia de esto es que si esa condición se satisface y entonces tenemos una cota superior para \max_x|\partial_x f(x,t)| y por lo tanto la ola no puede romper.

Bueno, ahora que sabemos cuándo la interfase no rompe cabe preguntarse si hay alguna situación en la que la interfase rompa. Y efectivamente obtenemos que hay datos tales que pasa lo siguiente:

Es más, podemos probar mediante una prueba asistida con ordenador, que existen datos iniciales tales que sólo rompen cuando la profundidad es finita. Es decir, que el fondo ayuda a que las olas rompan. Y si bien hemos probado estos teoremas en el caso de fluidos moviéndose en un medio poroso estos dos últimos resultados se pueden probar gratis para el caso de las water waves, i.e. la interfase entre un fluido incompresible e irrotacional siguiendo las ecuaciones de Euler y el aire.

–Referencias:

D. Córdoba, RGB, R.Orive, The confined Muskat problem: differences with the deep water regime.

–Nota: Con esta entrada participamos en el Carnaval de Matemáticas en su edición 26, organizado esta vez por ZTFNews.

–Nota 2: Con esta entrada participamos también en el Carnaval de Física en su edición XXXIV que organiza Hablando de Ciencia.

Problemas de frontera “no-tan-libre” en dinámica de fluidos: primeros pasos

Posted on by
2

Decía el señor Swett Marden que

“Un guijarro en el lecho de un pobre arroyuelo puede mudar el curso de un río”.

Parece una exageración y sin duda lo es, pero sirve para que nos hagamos la siguiente pregunta:

¿Cómo de importante es el lecho marino para las olas en la superficie?

Ésta es la pregunta que tratamos de contestar en este artículo. El problema que queremos entender es, dados dos fluidos incompresibles en un medio poroso acotado, ¿cómo se comporta la interfase entre ambos y que diferencias presenta con el caso en el que el medio no esta acotado? Bueno, vamos a trasladar ese problema físico a ecuaciones en derivadas parciales. Tenemos una densidad que presenta dos valores según estemos por encima o por debajo de la interfase, que denotamos por ,

Que los fluidos sean incompresibles y se muevan en un medio poroso acotado quiere decir que el dominio espacial de los fluidos es 

y que la velocidad satisface la Ley de Darcy y la condición de incompresibilidad

Estas ecuaciones se puede trasladar a una única ecuación para la interfase:

Ahora que tenemos el problema cabe preguntarnos si el hecho de que el dominio sea S y no \mathbb{R}^2 cambia mucho la situación. Para hacernos una idea podemos hacer unas simulaciones numéricas preliminares. Para ello consideramos un dato inicial y lo hacemos evolucionar en el caso donde el medio tiene profundidad finita (caso acotado) y también en el caso en el que el medio tiene una profundidad infinita (caso no acotado). Por supuesto el resto de los parámetros físicos son los mismos en ambas evoluciones. Así observamos lo siguiente

(Si no ves bien las imágenes pincha en ellas para hacerlas más grandes)

Parece claro a la vista de estos resultados que el hecho de que el medio esté acotado o no es relevante para las olas.

Una vez que tenemos el problema propuesto tenemos que empezar a sacar teoremas :-P. Evitando tecnicismos lo primero que probamos es

1) (Existencia y unicidad) que si el fluido de arriba es más ligero que el que está abajo el problema tiene una solución.

1.b) (Existencia y unicidad 2) que si el fluido de arriba es más pesado que el de abajo pero la interfase inicial es analítica existe una solución.

2) (Efecto regularizante) que dicha solución se vuelve muy regular (analítica) para cualquier t>0 (compárese con la ecuación del calor aquí.)

De momento estos 3 teoremas son idénticos en su enunciado a los teoremas cuando la profundidad es infinita. ¿Sorprendido? Bueno, esto sólo quiere decir que para probar matemáticamente las diferencias que hemos visto en los vídeos y las imágenes anteriores tenemos que trabajar un poco más, así que sed pacientes y esperad a la siguiente entrada ;-).

Bueno, si os veis muy impacientes podéis leer (o, en su caso, releer) ésta, ésta y esta entrada.

–Referencias:

D. Córdoba, RGB, R.Orive, The confined Muskat problem: differences with the deep water regime.

–Nota: Con esta entrada participamos en el Carnaval de Matemáticas en su edición 26, organizado esta vez por ZTFNews.

–Nota 2: Con esta entrada participamos también en el Carnaval de Física en su edición XXXIV que organiza Hablando de Ciencia.

Euler y el número e

Posted on by
1

Hoy hace 229 años que Euler murió en Rusia y a modo de recuerdo vamos a hablar hoy un poquito del número e y las finanzas, que es otro tema que está muy de moda con esto de la crisis económica.

Supongamos que tenemos un euro y que lo invertimos a un año con un interés del 100%. En éste caso nuestro euro al acabar de comernos las uvas se habrá convertido en dos euros. Si ahora consideramos que nuestra inversión tiene la mitad de interés (50%) pero que se paga cada 6 meses entonces a mitad de año tendremos 1+0.5 euros que invertimos de nuevo y obtenemos, tras comernos las uvas (1+0.5)(1+0.5)=(1+0.5)^2. Ahora supongamos que dividimos el tiempo tanto como queramos y vamos invirtiendo de nuevo lo que obtenemos, entonces, nuestra inversión se calcula como (1+\frac{1}{n})^n y se aproxima a 2,7182. ¿Os suena éste número o la expresión? Pues debería, ¡es el límite que define el número e que se estudia en bachiller! (al menos yo lo hice…)

–Nota: Sí, ya lo sabemos, esta entrada es una birria y además muy corta… Peeeeero prometemos escribir (al menos una y con suerte dos entradas) sobre Euler y el problema de Basilea para el Carnaval de Matemáticas que organiza esta vez ZTFNews. Y si queréis leer alguna curiosidad más sobre el número e para ir abriendo boca podéis empezar por la Wikipedia que tiene un artículo listando muchas de ellas.

Uno de los grandes de España aunque no fuese noble

Posted on by
Reply

Estoy hablando de Emilio Herrera. ¿No lo conocéis? Hasta esta semana yo tampoco. Y eso que es uno de los matemáticos importantes españoles. ¡Hasta fue amigo de Albert Einstein y vicepresidente de la RSME!. Mi amigo Pablo comenzó a hablarme de él y a contarme lo que había hecho y me parece una cosa tan genial como para escribir esta entrada (que es la primera entrada con tintes biográficos de esta bitácora).

Este señor era ingeniero del ejército y trabajó junto a Juan de la Cierva o a Leonardo Torres Quevedo (éste último fue matemático). La calidad de sus colaboradores ya nos indica su buen nivel (Juan de la Cierva inventó el autogiro y Leonardo Torres Quevedo el primer aparato controlado por radio). Que además de ser un gran ingeniero era extraordinario a otros niveles nos lo indica el hecho de que, antes de unirse a la República, pidiese al rey Alfonso XIII que le liberase de su juramento de fidelidad.

En lo científico su logro más importante es el diseño de un traje precursor de los trajes espaciales (cito de aquí):

Cuando la primera nave pisó el suelo de la Luna, Neil Armstrong recordó a Herrera, según relataría el español Manuel Casajust Rodríguez: “Me dijo que de no ser por el invento de mi maestro nunca habría llegado a la Luna”, explicó el discípulo a su regreso a España desde Cabo Cañaveral, donde Armstrong le regaló en señal de gratitud una de las rocas cosechadas en la superficie lunar durante su viaje.

Según refirió su ayudante, el piloto Antonio García Borrajo: “Cuando los norteamericanos le ofrecieron a Herrera trabajar para su programa espacial con un cheque sin limitaciones en ceros, él pidió que una bandera española ondeara en la Luna, pero le dijeron que sólo ondearía la de Estados Unidos”. Herrera rechazó la oferta.

Cuando Franco ganó la guerra civil se exilió fuera de España y vivió de sus patentes y colaborando con instituciones extranjeras como la Academia de Ciencias francesa o la UNESCO. Y para acabar de rematar su trayectoria ¡hasta fue presidente del gobierno republicano en el exilio!

Espero que os haya parecido un tipo tan genial como a mi mismo.

–Nota: La foto que ilustra esta entrada la he sacado de aquí.

–Nota 2: Con esta entrada participamos en el Carnaval de Física en su edición XXXIV que organiza Hablando de Ciencia.