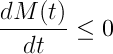Daily Archives: 25/09/2012

Euler y el problema de Basilea: Productos infinitos (I)

Posted on by
Reply

El día 18 de Septiembre hizo 229 años de la muerte de Leonhard Euler (ya lo dijimos aquí), así que ¿qué mejor momento para continuar con la serie sobre el problema de Basilea? Ésta serie ya consta de dos entradas (ver aquí y aquí) contando un poco cómo se formula el problema y qué avances se han dado. Vamos a resumirlo un poquito.

El problema de Basilea es calcular la suma de la serie


Jacob Bernoulli fue capaz de probar que la serie efectivamente convergía, i.e. que la suma tiene un valor finito. Una vez que se sabe eso uno puede ir sumando términos a ver qué número va quedando. El problema es que la serie converge muy despacio y hay que sumar muchísimos términos para tener una cantidad aceptable de decimales. Y es aquí donde entra Euler al escribir una serie equivalente que converge mucho más rápido, de manera que hay que sumar menos términos para obtener los mismos decimales.

Veamos qué hizo Euler llegados a este punto. Tenemos que recordar que si tenemos un polinomio

cuyas raíces (reales) son

 entonces podemos escribir 

Con esto en mente observamos que

 tiene cómo raíces 

Así Euler escribe, usando la serie de Taylor,

de donde, si dividimos por x y suponemos que podemos usar la propiedad anterior de los polinomios para una serie de potencias, obtenemos

Ahora basta observar que (3) nos da que el coeficiente que acompaña a x^2 es

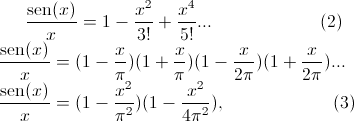
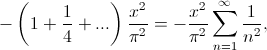
y ahora, igualando con (2), obtenemos el resultado

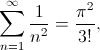
Éste resultado es correcto, pero tiene un enorme “pero”: el argumento es erróneo. No se puede hacer ese desarrollo como producto de las raíces para series. Por ejemplo podemos considerar

que, por tener las mismas raíces que el seno, ¡debería tener el mismo producto infinito! Esta prueba fue muy criticada por la comunidad y Euler siguió trabajando en desarrollos de productos infinitos para el seno de manera que pudiese acallar las quejas con una demostración completamente rigurosa y no sólo con un escueto “pues mi aproximación y el valor exacto que he calculado son iguales…”, pero eso lo dejaremos para otro día…

–Referencias:

Rafael Granero Belinchón, El problema de Basilea: Historia y algunas demostraciones. La Gaceta de la RSME, vol 12, num 4, pag 721-737, 2009.

E. Sandifer, Basel Problem with Integrals, MAA Online, 2004, disponible aquí.

Y aquí un conversor entre fórmulas de Latex e imágenes.

–Nota: Con esta entrada participamos en el Carnaval de Matemáticas en su edición 26, organizado esta vez por ZTFNews.

Problemas de frontera “no-tan-libre” en dinámica de fluidos: las diferencias

Posted on by
Reply

En esta entrada tratamos de presentar de manera sencilla la siguiente pregunta

¿Cómo de importante es el lecho marino para las olas en la superficie?

Así tenemos que estudiar el problema de la evolución de la interfase entre dos fluidos cuando dichos fluidos se encuentran en un medio poroso acotado y, tras hacer unas simulaciones para ver por dónde iban los tiros, dimos los primeros pasos en el estudio matemático del problema. Sin embargo, pese a que en las simulaciones observamos grandes diferencias en los primeros resultados matemáticamente rigurosos no capturamos esos fenómenos.

La primera pregunta que nos hacemos es ¿cuál es la evolución de la amplitud máxima de la ola? Para ellos lo que hacemos es estudiar

Lo que conseguimos probar es

o, lo que es lo mismo, que la amplitud no puede crecer con el tiempo. Este resultado es idéntico al caso donde la profundidad es infinita. Sin embargo en las simulaciones habíamos visto que las diferencias a este nivel eran grandes:

Lo que ocurre es que la velocidad a la que cae la amplitud es distinta. En el caso de profundidad infinita tenemos

donde f_0(x)=f(x,0) es la ola inicial. En el caso de un medio acotado la amplitud evoluciona según

Así hemos obtenido la primera diferencia importante: la interfase en el caso de profundidad finita decae más despacio. 

Ahora cabe preguntarse ¿cómo evoluciona \max_x|\partial_x f(x,t)|? Esta cantidad nos da una idea de cómo es la longitud de onda. Sabemos que en el caso donde el medio no está acotado se tiene que

si \max_x|\partial_x f(x,0)|<1 entonces \max_x|\partial_x f(x,t)|<\max_x|\partial_x f(x,0)|\;\; \forall t>0.

En el caso de que el medio tenga profundidad finita tenemos una condición (razonablemente complicada y que escribiremos F) que involucra no sólo a \max_x|\partial_x f(x,0)| si no también a \max_x|f(x,0)|:

si F(\max_x|\partial_x f(x,0)|,\max_x|f(x,0)|)\leq 0 entonces \max_x|\partial_x f(x,t)|\leq\max_x|\partial_x f(x,0)|\;\; \forall t>0.

Una consecuencia de esto es que si esa condición se satisface y entonces tenemos una cota superior para \max_x|\partial_x f(x,t)| y por lo tanto la ola no puede romper.

Bueno, ahora que sabemos cuándo la interfase no rompe cabe preguntarse si hay alguna situación en la que la interfase rompa. Y efectivamente obtenemos que hay datos tales que pasa lo siguiente:

Es más, podemos probar mediante una prueba asistida con ordenador, que existen datos iniciales tales que sólo rompen cuando la profundidad es finita. Es decir, que el fondo ayuda a que las olas rompan. Y si bien hemos probado estos teoremas en el caso de fluidos moviéndose en un medio poroso estos dos últimos resultados se pueden probar gratis para el caso de las water waves, i.e. la interfase entre un fluido incompresible e irrotacional siguiendo las ecuaciones de Euler y el aire.

–Referencias:

D. Córdoba, RGB, R.Orive, The confined Muskat problem: differences with the deep water regime.

–Nota: Con esta entrada participamos en el Carnaval de Matemáticas en su edición 26, organizado esta vez por ZTFNews.

–Nota 2: Con esta entrada participamos también en el Carnaval de Física en su edición XXXIV que organiza Hablando de Ciencia.