(Esta es una entrada par participar en el X Carnaval de Matemáticas (http://carnavaldematematicas.drupalgardens.com/) organizado por La Ciencia de la Mula Francis (o Francis (th)E mule Science’s News, http://francisthemulenews.wordpress.com/))
En esta entrada para nuestro blog (http://ambages.es/blog/) vamos a hablar de las posibles maneras de contar que se nos ocurren y sus aplicaciones a la integración.
Desde los primeros cursos en el Instituto nos hacen que aprendamos unas cuantas fórmulas para el cálculo de volúmenes y áreas de cuerpos o figuras más o menos “corrientes”, pirámides, conos, cuadrados, círculos… Más tarde, ya en Bachiller nos enseñan la genial herramienta que es la Integral de Riemann.
Este concepto es clave, por lo que vamos a gastar unas líneas recordándolo. Supongamos, por facilitar la exposición, que estamos calculando el área bajo una curva . Además,
es una curva curvada, nada de una linea recta o una poligonal. Lo que pensamos es, bueno, como sabemos la fórmula del área del rectángulo, vamos a ‘tapar’ el área bajo la curva con rectangulitos de distintos tamaños. Hecho esto observamos que el área calculada y el área que queríamos calcular no coinciden… pero si lo hemos hecho bien estarán muy cerca, si bien la que queremos calcular será un poquito mayor. La idea es ahora tapar ‘un poquito más’ del área buscada, para tener la certeza de que el área bajo la curva está entre dos valores aproximados y que son explícitos. Una vez hecho esto podemos tomar cada vez un mayor número de rectangulos para que nuestra estimación del área sea más precisa. Además argumentamos que en el límite cuando el número de rectángulos se hace infinito las 3 áreas, la buscada, la encontrada ‘por debajo’ y la encontrada ‘por arriba’, coincidirán.
Observamos que esto es válido para las curvas ‘razonables’. Como esta entrada es divulgativa no vamos a entrar en más detalles, pero es un ejercicio divertido (y fácil) tratar de encontrar una función que no se pueda integrar en el sentido de Riemann.
¿Qué os parece?, el cálculo de áreas, un problema central en la historia de la humanidad ya que está ligado a los campos de cultivo y por lo tanto al yantar, resuelto sin fórmulas complicadas ni nada parecido. Es cosa simplemente de ‘ir tapando con rectángulos’.
De esto ya se dio cuenta el genial Arquímedes (el que gritó ¡Eureka! y salió corriendo de la bañera). Así en su ‘Sobre la cuadratura de la parábola’ para calcular el área encerrada por un segmento de parábola lo que hace es tapar dicha superficie con triángulos isósceles de manera que lo que queda fuera de estos triángulos vuelven a ser segmentos de parábola similares al primero y de esta manera recurrente, sumando las áreas d elos infinitos triángulos calcular la superficie encerrada por la parábola inicial. Me gustaría señalar que la serie dada por las áreas de los triángulos es una serie geométrica de razón 1/4 y que Arquímedes la sumó entera. Es la primera vez en la historia (al menos que yo sepa) que se suma COMPLETA una serie geométrica (que es quizá la más fácil de las series), pues si bien en los Elementos de Euclides se da una fórmula para calcular la n-ésima suma parcial para cualquier n esto no es lo mismo que sumar la serie completa, hay una sutil diferencia.
Hasta ahora hemos hablado de integrales, áreas… pero nada de contar como dijimos al principio. Ahora vamos a eso. Supongamos que somos pobres becarios de investigación (lo de pobre es en sentido literal), y que queremos contar nuestro escaso peculio. Tenemos así monedas de 2 euros, de un euro, de 10 céntimos… vamos, de todas las monedas que hay. Una manera de contarlas es ponerse pacientemente, ir una a una e ir sumando. Primero cogemos una de 1 euro, luego una de 2 euros, luego una de 5 céntimos… Eso es lo que hace la integral de Riemann.
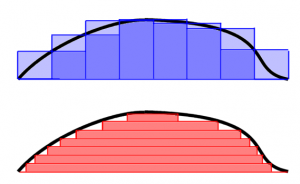
Pero esta manera de hacerlo no es la única. También podemos agrupar las monedas según su valor y contar cuantas tenemos en cada grupo. Así juntamos y nos salen 3 monedas de 2 euros por un lado, 10 monedas de 5 céntimos por otro… Ahora sólo hemos de multiplicar el número de monedas por su valor y sumar los resultados para cada grupo. Esta idea, para el cálculo integral, se llama Integral de Lebesgue. Lo que se hace es tapar con rectángulos según la altura de la función. Así en la figura adjunta (sacada de la wikipedia) se ve en azul la manera de integrar de Riemann y en rojo la manera de integrar de Lebesgue. Parece una tontería sin consecuencias, pero tiene unas consecuencias teóricas y prácticas importantisimas, de manera que es la Integral que los matemáticos usamos normalmente. Sin embargo, como es una entrada divulgativa, y no una clase de teoría de la medida lo voy a dejar aquí.