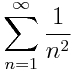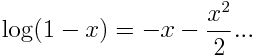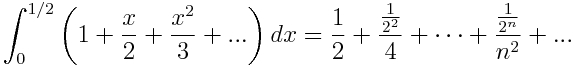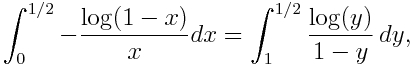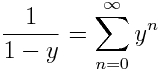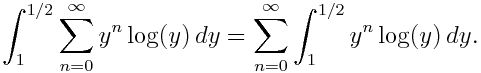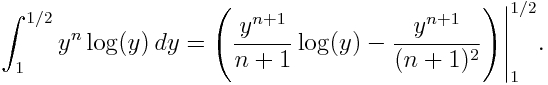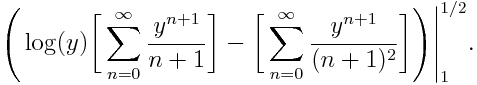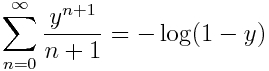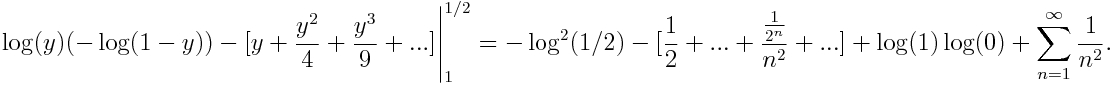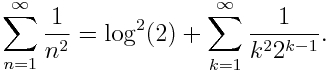Monthly Archives: March 2012

La importancia del orden

Posted on by
1

No nos referimos al (des)orden imperante en nuestras casas… Hablamos del orden de los términos de una serie. Y es que un resultado muy llamativo es que una serie, digamos \sum_{n=0}^\infty a_n convergente que no sea absolutamente convergente (es decir, tiene términos positivos y negativos y cumple que \sum_{n=0}^\infty |a_n|=\infty) si se reordena ¡¡se puede hacer que sume cualquier número!!

Teorema: Sea \sum_{n=0}^\infty a_n una serie tan que \sum_{n=0}^\infty a_n<\infty y \sum_{n=0}^\infty |a_n|=\infty. Entonces para todo A\in\mathbb{R} se tiene que existe g(n) tan que \sum_{n=0}^\infty a_{g(n)}=A.

¿Cómo podemos probar un resultado tan raruno? Bueno, veamos la idea, supongamos que A=\pi para fijar ideas. Dado que este mes ha sido el día de \pi esta elección tiene su gracia ;). Ahora sumemos términos positivos de la serie hasta exceder el valor de \pi. Ahora sumemos términos de signo negativo hasta que la suma parcial sea menor que \pi. Ahora volvemos a sumar términos positivos hasta exceder \pi y así sucesivamente. No diréis que no es ingenioso y llamativo.

–Nota 1: Esta entrada participa en el Carnaval de Matemáticas del mes de Marzo. Ésta vez ha sido organizado por Hablando de Ciencia

Euler y el problema de Basilea: La convergencia de la serie

Posted on by
1

En una entrada anterior (ver aquí) os contamos cómo Jacob Bernoulli encaró el problema de Basilea, esto es, la suma de la serie

Estamos en 1730 o 1731 y es ahora cuando hace su aparición Leonhard Euler, con su artículo De summatione innumerabilium progressionum, publicado en 1738, donde utiliza un método nuevo para aproximar esta serie. Euler parte de la serie de potencias de

La divide por -x e integra entre 0 y 1/2, obteniendo


En el lado izquierdo de esta expresión hace la sustitución y = 1-x consiguiendo  y reparando en que

se obtiene


Cada uno de los sumandos se puede integrar por partes,

Agrupando de nuevo, se consigue

Podemos ahora sustituir la serie de potencias

con lo cual queda

Ahora, Euler desprecia el producto \log(1)\log(0) y procede igualando la expresión de la derecha con el valor que se ha conseguido de la integral de la izquierda mediante el proceso anterior. De este modo llega a

Con estos manejos poco rigurosos, Euler solucionó el problema de la baja velocidad de convergencia de la serie: gracias a las potencias de dos en el numerador, los términos de la nueva serie que ha obtenido decaen mucho más rápido, y en consecuencia la convergencia de la serie es mucho mejor. Además, Euler conocía el valor de \log(2) con una gran cantidad de cifras decimales, consiguiendo así una aproximación 1.644934 que es correcta en las seis cifras decimales con la suma de sólo catorce términos de la nueva serie.

–Nota 1: Esta entrada participa en el Carnaval de Matemáticas del mes de Marzo. Ésta vez ha sido organizado por Hablando de Ciencia

–Nota 2: Para las imágenes con las fórmulas hemos usado el editor presente en esta web.

–Nota 3:  El texto anterior está basado en el artículo

Rafael Granero Belinchón, El problema de Basilea: Historia y algunas demostraciones. La Gaceta de la RSME, vol 12, num 4, pag 721-737, 2009.

Resultado de las votaciones

Posted on by
1

Bueno, ayer por la noche acabó el plazo para votar la mejor entrada del Carnaval de Matemáticas de Febrero (aquí el resumen actualizado). El resultado es el siguiente:

Felicidades al ganador :-). Nos vemos en el próximo Carnaval que organiza Hablando de Ciencia.