¿Cómo empezar bien el año? Pues recibiendo un premio. Esa ha sido la manera de comenzar el 2012 de Francisco Gancedo ya que la Real Academia Sevillana de Ciencias le ha concedido el premio “Real Maestranza de Caballería de Sevilla” por sus investigaciones en el estudio de problemas de frontera libre asociados a interfases entre fluidos incompresibles. O de otra manera: olas en diversas situaciones (puede leerse una entrada sobre el tema aquí).
¡Felicidades Paco!
El otro día, el Martes pasado concretamente, se anunciaron los Premios “Miguel Catalán”. Estos premios los da la Comunidad de Madrid al investigador más sobresaliente de todas las ciencias y tenemos el gusto de anunciar que el Premio en la categoría Jóven se lo ha llevado Diego Córdoba Gazolaz por sus trabajos en Mecánica de Fluidos. Algunos de los resultados en los que ha participado ya han sido anunciados aquí.
Nuestra más sincera enhorabuena desde aquí.
Buenas amigos. Ya sabemos que nos hemos dormido un poco este tiempo… ¡casi dos meses! En nuestra defensa hemos de decir que teníamos otros compromisos muy urgentes.
Tras disculparnos adecuadamente os mostramos los deberes: os dijimos en nuestra página de facebook que Antonio Córdoba Barba había sido galardonado con el Premio Nacional en Matemáticas y que nuestro amigo César tenía el gusto de entrevistarlo en su programa de radio “No es nuestra primera vez”. ¿Os acordáis? Bueno, pues para que el que se perdiese el programa pueda disfrutar, aún tarde, de él aquí está la prometida Entrevista con Antonio Córdoba.
En esta nueva entrada de la serie de las Paradojas (ver las otras entradas aquí ,
aquí y aquí) vamos a tratar de explicar paradojas que nacen de la mala interpretación de la probabilidad.
Todo el mundo conoce la serie C.S.I. y sus secuelas. En la serie un grupo de investigadores de la policía se dedican a buscar pruebas para resolver casos que sin el uso de avanzadas técnicas científicas y la participación de estos peritos forenses sería imposible solucionar. Los capítulos de la serie cuentan el asesinato y cómo los miembros del C.S.I. han recabado las pistas y acaban con la detención del culpable. Sin embargo hay una última parte que nunca tratan. Me refiero al juicio. Y es que, aunque tal cual está en la serie parece obvia la culpabilidad dadas las pruebas que se han encontrado, la valoración de las evidencias es un tema peliagudo en extremo.
El problema si lo escribimos de manera matemática involucra probabilidades condicionadas. La definición de este objeto (sacada de la wikipedia) es, dado un espacio de probabilidad 
Hemos de pensar en B como en que ha ocurrido algo que modifica la información que tenemos disponible.
Así, si dado un caso de los de la serie de televisión, consideramos los sucesos
1) “se encuentran evidencias”. Este suceso se escribe E
2) “el sospechoso es culpable”. Este suceso se escribe C.
3) “el sospechoso es inocente”. Este suceso se escribe I.
4) “el sospechoso es inocente dado que hemos encontrado la prueba E”. Este suceso lo escribimos como 
y
5) “el sospechoso es culpable dado que hemos encontrado la prueba E”. Este suceso lo denotamos por 
Así la probabilidad que le interesa al juez con sobrecarga de trabajo que le toque es
Vamos a motivar nuestra nueva entrada sobre paradojas con un caso famosísimo en su época: el caso Dreyfus (ver esta página para más detalles). Esta novela por entregas tiene de todo, un bueno inocentón, el propio Dreyfus, un malo malísimo con multitud de problemas, Esterházy, y hasta cameos de personajes famosos como por ejemplo Zola. Un brevísimo resumen: tras la guerra franco-prusiana del siglo XIX se detectó una filtración en el ejército francés. Se detuvo al Capitán Alfred Dreyfus. Se tenía como principal evidencia una carta. Lo que ocurrió es que un “perito” estimó la probabilidad de coincidencia entre la letra de la carta y la letra del Capitán Dreyfus, suponiendo que Dreyfus fuese inocente, como 0.2. Como este mismo perito había observado 4 coincidencias y éstas se asumían independientes (es decir, que la probabilidad de las cuatro es el producto de las cuatro probabilidades) el perito conluyó que Dreyfus era culpable porque, según él, “la probabilidad de que fuese inocente dada la evidencia (las coincidencias entre la carta y la letra de Dreyfus) es muy pequeña”. El lector avispado se habrá dado cuenta del truco. El perito “estima” (que esa es otra cosa, ¿por qué la probabilidad es 0.2?) 
Veamos qué implicaciones tiene la asunción 
y, similarmente,
Ahora consideramos la cantidad
Si ahora usamos la hipotesis de que 
¿Cuál es la moraleja? Pues que la probabilidad no es intuitiva nunca (o casi nunca) y que todos los argumentos probabilísticos deben ser cuidadosamente repasados. Si no lo hacemos así nos arriesgamos a repetir tristes historias (ver esta entrada de la wikipedia o esta otra).
–Referencias: 1) Estadística y Evaluación de la Evidencia para Expertos Forenses. Segunda Edición. C. Aitken y F. Taroni. (Traducido por: J. Lucena, L. Gil y R. Granero), Ed. Dykinson.
— Con esta entrada participamos en la edición 2.7 del Carnaval de Matemáticas, que está organizado por La Aventura de la Ciencia.
En esta nueva entrada de la serie de las paradojas (las primeras estradas son http://scientiapotentiaest.ambages.es/?p=244 y http://scientiapotentiaest.ambages.es/?p=266) nos vamos a centrar en las paradojas que vienen de la probabilidad. Y es que la probabilidad pese a ser algo bastante mencionado en la vida diaria no es entendida por mucha gente.
Voy a comenzar tratando el problema de Monty Hall. Este problema es muy divertido, porque todo el mundo al que se lo contemos dirá que es muy intuitivo. ¡El problema es que para cada uno será intuitiva una respuesta distinta!
Supongamos que estamos en un programa de estos de la tele. En este programa hay tres puertas. Una de las tres tiene un premio y las otras dos no tienen nada. La puerta que tiene el premio se elige al azar de manera equiprobable. El juego consiste en elegir una puerta. Tras nuestra elección, el presentador, que sabe dónde está el premio, abre una de las dos puertas que no hemos elegido y que no tiene nada. Tras esto nos pregunta si queremos cambiar de puerta. La pregunta viene ahora, ¿qué nos sale mejor como jugadores? ¿cambiar nuestra primera elección o dejarla estar?
Observamos que el premio no cambia de puerta mientras nosotros jugamos.
La respuesta correcta es que siempre nos sale mejor cambiar de puerta. Sí, amigos lectores, es mejor cambiar. ¿Qué no me creéis? Vamos a ver si os convenzo. Como el premio está en una de las puertas de manera equiprobable la probabilidad de que el premio se encuentre en la puerta que hemos elegido al comenzar a jugar es 1/3. Ahora el presentador abre una de las otras dos puertas sin descubrir el premio. ¿Cuál es la probabilidad de que nuestra puerta esconda el premio? LA MISMA, 1/3. Por lo tanto si cambiamos de puerta nuestra nueva elección tendrá probabilidad 2/3. Vamos a ilustrar esto un poco más mirando los posibles casos. Vamos a suponer que elegimos siempre la puerta 1, como todo es simétrico todos los casos estarán reflejados igualmente.
1) El coche está en la puerta 1.
1.a) Cambiamos de puerta y perdemos.
1.b) No cambiamos y ganamos.
2) El coche está en la puerta 2.
2.a) Cambiamos de puerta y ganamos.
2.b) No cambiamos y perdemos.
3) El coche está en la puerta 3.
3.a) Cambiamos de puerta y ganamos.
3.b) No cambiamos y perdemos.
Hagamos el recuento: Si cambiamos ganamos 2 veces frente a una que perdemos. Si no cambiamos la situación es recíproca. Como hay 3 casos posibles la probabilidad de ganar cambiando es 2/3.
Otra manera de convencerse es aumentar el número de puertas. Supongamos que tenemos 100 puertas. Entonces la probabilidad de que el premio esté en nuestra puerta es 1/100. Tras elegir, el presentador abre todas las puertas menos dos, la que tu elegiste y otra, de manera que ninguna de las abiertas mostrase el premio. Ahora parece claro que lo mejor es cambiar.
Otra paradoja que invariablemente se estudia en los cursos iniciales de probabilidad es la paradoja de los hijos (a falta de un nombre mejor en castellano). Supongamos que la probabilidad de que nazca un chico o una chica es la misma, 50%, y que el sexo de cada hijo es independiente del sexo de los demás hermanos. Vamos con el problema. La señora López tiene dos vástagos. Supongamos, a modo de calentamiento, que el hijo mayor de la señora López es un niño, ¿cuál es la probabilidad de que el menor sea niña? La respuesta, claro, es 50%. Ahora se nos plantea un problema ligeramente distinto: Supongamos que uno de los hijos de la señora López es niño, ¿cuál es la probabilidad de que el otro hijo también sea niño? ¿50%? Veamos los casos tal cuál está escrito (observando que la familia está fija para los más puntillosos) y ordenando los niños por edad:
1) Chico-chico
2) Chica-chico
3) Chico-chica
Hay 3 casos posibles y sólo 1 es el que nos preguntan. Como son equiprobables la probabilidad de que ambos hijos de la señora López sean niños es 1/3. El truco aquí está en que al decir que uno de los hijos es chico perdemos información sobre su edad. En la primera pregunta tenemos más información y podemos descartar más casos.
La probabilidad se va descubriendo un poco farragosa y “extraña” en ocasiones. Sin embargo todavía no hemos tratado la principal fuente de problemas al tratar con la probabilidad. Me refiero a la ambigüedad. Las palabras “al azar” no tienen un significado preciso y se usan con más asiduidad de la recomendable. Esto quedó claramente expuesto en la obra de J. Bertrand “Calcul des probabilités”. En este manual propuso un enunciado y dio varias respuestas al problema, todas bien lógicas y correctas. El problema era que en cada uno la definición de “al azar” era distinta. Es ahora cuando nos ponemos técnicos. En la entrada anterior ya mencionamos cosas como “medidas” de conjuntos (ver la entrada anterior). Eso nos volverá a ser útil, pues la manera matemática de dar sentido a las palabras “al azar” utiliza esas ideas. En matemáticas un “espacio de probabilidad” es un espacio de sucesos posibles en nuestro experimento, una manera de agruparlos en conjuntos y una manera de “medir la probabilidad” cada uno de estos conjuntos de sucesos. Claro está que la definición precisa es mucho más técnica. Así la idea que quiero dejaros es que esas tres cosas abstractas es lo que da sentido a la palabra “azar”.
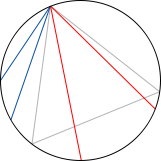
El ejemplo que más me gusta de esto es la paradoja de Bertrand. Consideremos un círculo con un triángulo equilatero inscrito. La pregunta ahora es ¿cuál es la probabilidad de que una cuerda trazada “al azar” sea más larga que los lados del triángulo? Veamos las tres maneras clásicas de calcular dicha probabilidad:
1) Supongamos, sin pérdida de generalidad, que uno de los extremos de la cuerda coincide con uno de los vértices del triángulo. En ese caso al quedar la circunferencia dividida en 3 trozos iguales y coincidir uno con el conjunto donde la cuerda es más larga que el lado del triángulo concluimos que la probabilidad pedida es 1/3. Aquí el espacio de sucesos es el conjunto de puntos de la circunferencia y la medida de probabilidad asociada es la longitud del arco considerado dividido la longitud total de la circunferencia.
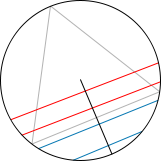
2) Consideremos ahora un radio perpendicular a uno de los lados del triángulo. Esto de nuevo nos facilita la vida pero no perdemos generalidad. Ahora trazamos la cuerda de manera perpendicular a dicho radio por un punto aleatorio del mismo. La probabilidad de que la cuerda sea mas larga que el lado es justamente 1/2 si la trazamos con estas reglas. Aquí el espacio de sucesos es el conjunto de puntos del radio y la medida de probabilidad es la longitud del segmento considerado dividido por la longitud total.
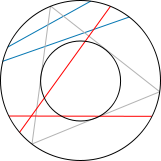
3) Ahora nuestro experimento consiste en elegir el punto medio de la cuerda. Si trazamos la cuerda con esta regla la probabilidad de que la longitud de la cuerda sea mayor que la del lado del triángulo es la misma que la probabilidad de que el punto medio de la cuerda esté en un círculo concentrico inscrito en el triángulo de radio la mitad (y área 1/4 del área del círculo original). Por lo tanto la probabilidad será 1/4. Aquí el espacio de sucesos es el conjunto de puntos del círculo y la medida de probabilidad es el área del conjunto de puntos considerado dividido entre el área del círculo original.
La paradoja aquí estriba en que para una pregunta tenemos tres respuestas. Además, eligiendo la definición de “azar” todas son correctas.
Creo que ha quedado claro que cuando decimos cosas como “aleatorio” o “al azar” no estamos en realidad diciendo nada y que debemos entrar, aunque no queramos, en tecnicismos para evitar este tipo de paradojas.
— Nota: Las imágenes han sido obtenidas de la Wikipedia en inglés
— Nota: Con esta entrada participamos en el Carnaval de Matemáticas en su edición 2.6 (albergado por “La vaca esférica” , http://lavacaesferica.com/).
Otra entrada dedicada a las paradojas. Continuamos con la tónica de la entrada anterior (http://scientiapotentiaest.ambages.es/?p=244) por lo que nos restringiremos a aquellas paradojas que son producidas por la idea del infinito o de los infinitésimos (lo “infinitamente” pequeño), aunque esta vez abordaremos la teoría de la medida y la teoría de conjuntos.
Esta entrada es un poco más avanzada, y se requieren algunos conocimientos de matemática. Sin embargo, intentaremos dar algunas explicaciones que no necesiten estos conocimientos.
Primero vamos a tratar la sorprendente afirmación de que podemos construir un conjunto con medida cero que es no numerable y no es vacío. Sé que esto no es una paradoja, pero también sé que muchos matemáticos acaban la carrera sin entender este conjunto y que, sea o no paradoja, el enunciado es desconcertante. La idea es que podemos asignar medidas a conjuntos, por ejemplo el intervalo [0,1] mide 1, el conjunto de los irracionales del intervalo [0,1] también mide 1. Detengámonos en esto un poco más. Sabemos que un punto sólo no mide nada. Tenemos como hipótesis que si dos conjuntos no se intersecan la medida de la unión es la suma de las medidas, por ejemplo si consideramos el intervalo [0,1] y el [2,3] la medida es 2. No ocurre lo mismo si consideramos los intervalos [0,1] y [0.5,1.5], porque tienen un subintervalo en común. Además supondremos que esta propiedad se puede extender a uniones (y sumas) numerables (con un número infinito de conjuntos, pero no hay más conjuntos que números naturales).
Si ahora leemos (y quizá releemos) esto otra vez nos damos cuenta de que una unión numerable de puntos por fuerza ha de ser disjunta (porque los puntos, o son el mismo, o son distintos) y por lo tanto, aplicando la propiedad, el conjunto formado por dicha unión tendrá medida cero. Esto es algo bastante razonable si lo desvestimos de parte de su rigor, ¿quién apostaría a que el conjunto de los números enteros en la recta mide algo? ¿quién me diría lo que mide?. A poco que pensemos llegaremos a la conclusión de que la única manera razonable de asignarle una medida a dicho conjunto es diciendo que es cero.
Ahora la sorpresa es que este tipo de conjuntos, ‘pequeños’ y ‘dispersos’ no son los únicos conjuntos que miden cero.
Existe (al menos) un conjunto no numerable con medida cero.
El problema de este conjunto es la ‘dispersión’. Tiene bastantes puntos como para medir algo, pero simplemente no estan “juntitos”.
En palabras de Ian Stewart, “vamos a construir el conjunto de Cantor como harían los ratones”.
Tomamos el conjunto [0,1]. Lo dividimos en tres segmentos iguales y le quitamos el segmento central. A cada uno de los dos segmentos resultantes le hacemos lo mismo y así sucesivamente. El conjunto de Cantor es el límite así conseguido.
Veamos cuanto mide. La medida de cada segmento es 1/3, por la propiedad anterior la medida total en el primer paso de la iteración es 2/3. En el segundo paso de la iteración tenemos que cada uno de los intervalos ha perdido un tercio de su longitud, por lo que mide dos tercios de su longitud. En total en el segundo paso de la iteración el conjunto mide 
Si vemos que es no numerable hemos concluido. Recuerdo que ser no numerable es tener un cardinal (el número de elementos) infinito mayor que el de los números naturales. Esto es un poco ingenioso, pero no es difícil. Veamos, tenemos, por estar el conjunto de Cantor contenido en el intervalo unidad, que el cardinal será menor o igual. Por lo tanto si demostramos el mayor o igual hemos concluído la igualdad. Observamos que nuestra construcción de ir eliminando segmentos es equivalente a escribir todos los números en base 3 y eliminar aquellos que tienen algun 1 en su expansión. Por ejemplo el 0.222… (ojo está en base 3) está en nuestra construcción, pero el 0.11 no lo está. Ahora pensamos en base dos y vemos que nuestros número, los que forman el conjunto en realidad son ‘binarios’ si cambiamos los doses de su expansión por unos. Por ejemplo el punto 0.222… en base 3 pasa ahora a ser 0.1111… Ésta es nuestra función, cambiar los doses por unos. Ejercicio: Razonar por qué es suprayectiva.
¡Tachán!. Hemos concluído, hemos construído un conjunto no numerable que mide cero. Desmontamos así nuestra hipótesis inicial que era asociar la idea de medida con la de cardinalidad y concluir que si tenía un cardinal como el de los naturales (un número de elementos igual) entonces media cero y estos eran todos. Además del ‘tamaño’ tenemos que considerar también la ‘dispersión’.
Sigamos con paradojas, ahora de cardinales (el número de elementos de un conjunto, recuerdo).
Ahora hay que entrar en materia más seria de cardinales, así que voy a dar una definición más rigurosa no del concepto de cardinal en sí, que está clara: es el número de elementos de un conjunto, sino de la propia manera de contar. Diremos que dos conjuntos tienen el mismo cardinal (tamaño) si existe una función biyectiva (es decir, que va de uno a uno) entre ambos. Esta idea tan simple es la única que nos permite tratar con distintos tamaños infinitos. La idea es que, si queremos contar el número de alumnos en una clase, podemos contar el número de mesas y ver si hay tal función. En el caso de que haya más alumnos la función no será inyectiva, pues habrá dos alumnos en alguna mesa. En el caso de que sobren mesas lo que no será la función es suprayectiva. Observamos que las nociones de inyectividad y suprayectividad son en realidad nociones de ‘tamaños’ si las usamos así.
La última paradoja de Zenón de Elea (ver entrada http://scientiapotentiaest.ambages.es/?p=244), la paradoja de la flecha:
Lanzamos una flecha. En cada instante de tiempo ésta no se mueve, pues no le da tiempo.
Ahora Zenón razonaba que al haber una suma de ceros el resultado seguía siendo cero, y por lo tanto no hay movimiento. Aunque esta paradoja se puede desmontar con el concepto de derivada, voy a optar por razonar con teoría de la medida, para ello he de introducir unos conceptos.
¿Cuánta longitud tiene un punto sólo?. La respuesta es que ninguna, un punto no tiene dimensión alguna. Ahora bien, también se puede demostrar que si tenemos infinitos puntos, pero un infinito pequeño (como los números naturales) volvemos a tener cero. Es decir la longitud que suman infinitos (pero un infinito como el de los naturales) puntos es cero. Sin embargo, el intervalo [0,1] tiene longitud exactamente 1, y no es más que un conjunto de puntos en fila. ¿Dónde está el truco?, os dejos pensarlo 3 segundos… El truco está en la cantidad de puntos, el intervalo [0,1] tiene infinitos puntos, pero es un infinito mucho mayor que el de los naturales. Para convencernos de esto podemos considerar que los puntos 
¿Cuál es la conclusión? Es cierto que una suma de ceros es cero, ¡siempre que no sumemos demasiados!, si sumamos un número infinito (de un infinito como la cantidad de puntos del intervalo [0,1]) entonces el resultado puede ser un número finito y no cero, pero peor aún, puede ser infinito (pensad en la longitud de toda una recta).
Concluímos que la flecha se mueve, pues si bien estamos sumando ceros, sumamos muchos, ya que los instantes de tiempo son como el intervalo [0,1] y no como los naturales.
Hemos desmontado, junto con la entrada anterior (http://scientiapotentiaest.ambages.es/?p=244), las 3 paradojas de Zenón. En las próximas entradas veremos más paradojas y cómo evitarlas (si se puede).
Veamos otra paradoja basada en el mismo problema.
Todos los números (naturales) no son cuadrados perfectos, sin embargo, hay tantos números (naturales) como cuadrados perfectos.
Esta paradoja se conoce como paradoja de Galileo, y reposa en la existencia de dicha función. Consideramos ambos conjuntos, los cuadrados y el conjunto de los números naturales que lo contienen. Claramente el número de cuadrados es menor o igual al número total de números naturales. Sin embargo, por cada número natural hay un cuadrado y entonces dicha función ha de ser biyectiva.
Leedlo con atención, no es fácil la primera vez. Huelga decir que los mismo se puede hacer para los enteros, los primos, los pares… El primer momento en el que falla es al considerar los irracionales.
Vamos a por la última paradoja, que si hemos entendido la de Galileo es fácil. Ésta se llama paradoja de Hilbert.
Si tenemos un hotel de infinitas habitaciones, completo, y llega un nuevo turista podemos darle habitación.
y más aún
Si en nuestro hotel de infinitas habitaciones, completo, aparecen infinitos nuevos clientes, también podemos darles habitación.
Estas paradojas no las voy a resolver explícitamente; sin embargo, su respuesta ya está escrita. Como pista voy a decir que se piense en los naturales como las habitaciones y desde ahí se busque un conjunto para nuestros clientes en cada caso. Se puede observar que esta paradoja es justamente “simétrica” a la construcción del conjunto de Cantor: en el conjunto de Cantor quitamos elementos del intervalo [0,1] y al final nos queda algo con el mismo cardinal. ¡En esta paradoja añadimos elementos y nos queda algo con el mismo cardinal!
Con esta última paradoja tengo un chascarrillo. Cuando estudiaba primero de la ESO, en el instituto de Mota del Cuervo, un maestro nos contó justamente esta paradoja. El hombre nos repetía eso de los conjuntos de ‘tamaños’ diferentes, pero en ningún momento mencionó nada de funciones, inyectividad… Todo parecía muy extraño hasta para el maestro. Yo me fui a mi casa sin entenderlo y con la idea de que el maestro tampoco se enteraba. No volví a acordarme de esto hasta hace un par de años, cuando estaba corriendo y me vino a la cabeza. ¡Os juro que aún no estaba muy cansado por la carrera!
En la próxima entrada querría hablar de algunas paradojas en probabilidad, como la del cumpleaños y la de Bertrand.
PD: La imágen ha sido tomada de la entrada de la Wikipedia http://en.wikipedia.org/wiki/Cantor_set .
Voy a escribir una serie de artículos que traten las diversas paradojas que hay; si no todas, al menos las más conocidas. Creo que es justo empezar con las de Zenón, al menos con algunas de ellas, ya que son las más antiguas de las que tengo constancia. También, porque es fácil ver donde está la argucia.
Zenón de Elea (ver aquí) intentaba demostrar que no podía haber movimiento, que este era sólo una ilusión. Para ello, propuso una serie de paradojas que “probaban” su punto de vista.
El veloz Aquiles compite contra una tortuga, la velocidad de Aquiles es doble que la de la tortuga, y éste, seguro de su victoria, le da ventaja.
Zenón razonaba lo siguiente, como la tortuga en el tiempo (cada vez más pequeño) que Aquiles se mueve se mueve a su vez (aunque sea un movimiento diminuto enseguida) Aquiles nunca la alcazará, pues siempre irá un épsilon por detrás.
Podemos resolver la paradoja de dos maneras, considerando series, y considerando espacios discretos. Por discretos quiero decir que Aquiles dé zancadas de longitud fija. La segunda no tiene interés, pues por la cuenta de la vieja sale fácil, además no enlaza tan bien como la otra para introducir conceptos (salvo que uno esté pensando ya en cuantización). Veamos como se resuelve con series.
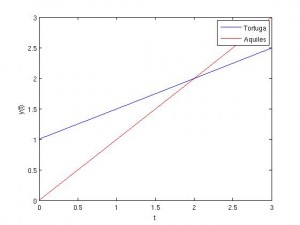
A ver, si Aquiles le da 1 de ventaja a la tortuga, entonces cuando Aquiles va por su primer metro la tortuga va por 1.5, cuando Aquiles va por 1.5 la tortuga va por 1.75… Veamos cuanto recorre la tortuga. La tortuga en tiempo 0 está en 1, en tiempo 1 está en 1.5 y así sucesivamente, la tortuga recorre por lo tanto 
Concluímos que Aquiles alcanza a la tortuga en
En este caso en particular, con estas velocidades, esta ventaja… estaba claro desde el principio: no había que meterse en follones de series, pues otra vez la cuenta de la vieja nos vale. En lugar de considerar tiempos cada ez más pequeños, consideremos los tiempo estándar del problema. En este caso si la tortuga avanza uno y Aquiles dos metros por segundo, y Aquiles le dió un metro de ventaja a la tortuga, entonces en un segundo la tortuga está en el metro 2, que es justamente donde está Aquiles.
Veamos esto con un dibujo. La velocidad de la tortuga es 1/2 (en las unidades de Aquiles), y su posición inicial es y=1. Por lo tanto, tenemos que su posición en cada tiempo viene dada por la recta y=1+t/2. Para Aquiles tenemos que su velocidad es 1 (estamos usando sus unidades) y su posición inicial es y=0. Por lo tanto su recta es y=t. Comprobamos que en t=2 las rectas se cortan, por lo tanto Aquiles se encuentra con la tortuga.
Otra de las paradojas que Zenón utiliza es la la de la dicotomía
Aquello que se mueva entre dos puntos, ants de cubrir toda la distancia debe cubrir la mitad, y antes la mitad de la mitad…
Zenón argumentaba que al continuar hata el infinito no podía haber movimiento, pues necesitaría tiempo infinito. Ya hemos visto que usando series de desmontaba la anterior, y esta tiene la misma pinta, pues todo el problema es si la sucesión de tiempos me da una serie convergente, en cuyo caso, el valor de la suma será el tiempo empleado en movernos entre esos dos puntos.
Consideremos que avanzamos a velocidad fija de un metro por segundo entre el punto A y el B, separados por una distancia de un metro. En este caso tenemos que los tiempos que tardamos en recorrer las sucesivas ‘medias partes’ del recorrido es justamente la longitud del trozo en cuestión. Veamos, la sucesión de distancias recorridas es 
¿Por qué hemos de considerar series aun en casos tan simples? pues porque lo importante, y lo que acaba de desmontar estas paradojas es el concepto de convergencia[negrita], la clave es que una suma de infinitas cosas bajo ciertas condiciones puede tener una suma finita.
Era eso lo que Zenón no tenía nada claro; él veía infinitos tiempos y decía: “no puede ser que nos movamos, pues tardaríamos un tiempo infinito”.
Hemos desmontado 2 de las paradojas de Zenón. Dejaremos para otro post una manera de desmontar la tercera paradoja, pues para ello necesitamos saber que existen distintos tipos de infinitos.
En las próximas entradas de esta serie, veremos más paradojas y cómo evitarlas (si se puede).
Esta entrada es la gemela de la entrada Introducción al cálculo variacional en la física (http://scientiapotentiaest.ambages.es/?p=87). En ella David nos decía
Queremos saber qué camino tomará un cuerpo en una cierta situación. Imaginemos que tenemos una cantidad (un funcional, matemáticamente hablando), a la que llamaremos acción (con unidades de energía por segundo), que depende del “camino” que ese cuerpo toma en su movimiento. Esa acción puede ser calculada para cada cualquier camino siempre y cuando tenga una cierta regularidad. Pues bien, el camino real, el que tomará el cuerpo y que podrá ser predicho, es aquel que hace de la acción un mínimo (más rigurosamente, un valor estacionario).
Así, el enfoque en mecánica clásica es: dado un sistema físico, obtenemos un funcional; a este funcional se le calculan los puntos críticos y esos puntos críticos nos dan las soluciones del problema. Matemáticamente esto es ir del funcional a la ecuación diferencial.
Veamos esto con un ejemplo: Supongamos que tenemos una partícula de masa unidad bajo el influjo de un potencial 
Entonces el Lagrangiano se define como
donde 
Ahora definimos la acción como ![A[x]=\int_0^t L(x)dt.](http://s0.wp.com/latex.php?latex=A%5Bx%5D%3D%5Cint_0%5Et+L%28x%29dt.&bg=T&fg=000000&s=0 "A[x]=\int_0^t L(x)dt.")
Una vez tenemos la acción, queremos minimizarla. Para esto hemos de encontrar los puntos críticos. Si fuese una función de una variable normal y corriente derivaríamos e igualaríamos a 0. Derivar es encontrar el cambio de una cantidad cuando se varía otra de manera infinitesimal. Aquí la idea es similar. Lo que hacemos es, dada una perturbación con los extremos fijos (
Ahora pensamos la acción para esta nueva curva 
=\int_0^t L(y(t))dt](http://s0.wp.com/latex.php?latex=A%5By%5D%28s%29%3D%5Cint_0%5Et+L%28y%28t%29%29dt&bg=T&fg=000000&s=0 "A[y](s)=\int_0^t L(y(t))dt")
y obtenemos el cambio en ella cuando variamos ligeramente s; esto es, derivamos en 
Calculamos, utilizando la regla de la cadena,
Sustituyendo obtenemos 
Esta integral debe ser 0 para que nuestra 
Estas consideraciones nos imponen una relación entre las derivadas 
que es, nada más y nada menos, la segunda ley de Newton.
Este enfoque va desde el funcional, que se obtiene con consideraciones físicas, a la ecuación diferencial. O de otra manera, se usa una ecuación diferencial para solucionar un problema de minimizar un funcional.
Sin embargo también existe el método inverso. Supongamos que tenemos una ecuación diferencial (generalmente en derivadas parciales) como puede ser
con 
Demostrar la existencia de solución para la ecuación original es lo mismo que conseguir un punto crítico de nuestro funcional. Si además probamos que es único entonces la ecuación tendrá una única solución. Así con este enfoque vamos desde la ecuación al funcional.
Y como seguir abundando en este tema puede ser muy técnico lo dejaremos aquí por el momento.
\bigg{|}_{s=0}=\frac{d}{ds}\left(\int_0^t L(y(t))dt\right)\bigg{|}_{s=0}](http://s0.wp.com/latex.php?latex=%5Cfrac%7Bd%7D%7Bds%7DA%5By%5D%28s%29%5Cbigg%7B%7C%7D_%7Bs%3D0%7D%3D%5Cfrac%7Bd%7D%7Bds%7D%5Cleft%28%5Cint_0%5Et+L%28y%28t%29%29dt%5Cright%29%5Cbigg%7B%7C%7D_%7Bs%3D0%7D&bg=T&fg=000000&s=0 "\frac{d}{ds}A[y](s)\bigg{|}_{s=0}=\frac{d}{ds}\left(\int_0^t L(y(t))dt\right)\bigg{|}_{s=0}")
