Category Archives: Matemáticas

Las olas: Un matemático en la playa.

Posted on by
7

Ya va haciendo calor y empieza a apetecer el irse a la piscina o a la playa. Sin duda la playa es uno de los sitios menos entendidos por el mundo científico y más visitados por el resto del mundo. El fenómeno al que me refiero cuando digo que no se comprende completamente, claro está, son las olas. En esta entrada estudiaremos diversos casos de olas entre fluidos ilustrando el texto con diversos videos.

[iframe: width=”400″ height=”320″ src=”http://www.youtube.com/embed/GEl-Qu7ApGQ” frameborder=”0″ allowfullscreen]

Vamos a empezar hablando de un caso un poco más general que las típicas olas en la superficie del mar. En matemáticas entendemos por interfase entre fluidos a la parte donde estos entran en contacto entre sí. Así una ola es la interfase entre el aire y el agua. Una interfase entre fluidos con distintas propiedades puede exhibir un comportamiento muy complicado, patológico si se quiere, pero que es, pienso yo al menos, visualmente muy bonito. Estoy pensando por ejemplo en singularidades como pueden ser las llamadas singularidades de Kelvin-Helmholtz o Rayleigh-Taylor. Hagamos una parada antes de proseguir con nuestras olas.

Supongamos por un momento que tenemos dos fluidos con densidades distintas, por fijar ideas digamos aceite y agua, de manera que el fluido más denso (el agua) está en el fondo de un recipiente cerrado completamente (un tubo con ambos extremos taponados). El fluido menos denso (el aceite) reposa encima del agua. Supongamos ahora que dicho tubo, y por tanto los fluidos, está en reposo, por ejemplo en una mesa. La pregunta es ¿qué ocurre si, repentinamente, inclinamos dicho recipiente? Veamos unos vídeos con este experimento:

[iframe: width=”400″ height=”320″ src=”http://www.youtube.com/embed/CL7s8h7mtPE” frameborder=”0″ allowfullscreen] [iframe: width=”400″ height=”320″ src=”http://www.youtube.com/embed/ggEp4n6Bhps” frameborder=”0″ allowfullscreen] [iframe: width=”400″ height=”320″ src=”http://www.youtube.com/embed/1XqJJfw63zQ” frameborder=”0″ allowfullscreen]

Lo que vemos en el video es que la interfase “se enrolla” sobre sí misma. Esto es debido a que las velocidades (que son un vector en 3D) tangentes a la interfase tienen signo distinto. Es decir, si lo pensamos en una interfase en 2D (una curva) sería que la velocidad en el fluido que está encima de la interfase “señala hacia la izquierda” mientras que para el fluido que está debajo de la interfase “señala a la derecha”. De ahí esa tendencia a girar y enrollarse.

Supongamos ahora que cambiamos el orden de los fluidos. Ahora tenemos (por ejemplo porque tenemos una barrera entre ambos fluidos) el agua reposando sobre el aceite. ¿Qué ocurre si retiramos rápidamente la barrera entre ambos fluidos? Bueno, pues que el fluido más denso, por la gravedad, caerá hacía abajo, empujando en su camino al fluido menos denso, que subirá hacía arriba. Vale, el caso es que lo que va a ocurrir es sencillo de vaticinar, lo curioso aquí es la manera en que ocurre. Vayamos otro rato a youtube…

[iframe: width=”400″ height=”320″ src=”http://www.youtube.com/embed/VlAzyVx7N9M” frameborder=”0″ allowfullscreen] [iframe: width=”400″ height=”320″ src=”http://www.youtube.com/embed/8EkFL-8wIUI” frameborder=”0″ allowfullscreen]

Tras ver estos experimentos y haber pensado un poquito nos damos cuenta de que el que quiera entender bien estos procesos tiene mucho trabajo por delante. Y ahí estamos bregando algunos…

Volvamos a las olas. Hace tan sólo unos días uno de mis jefes (Diego Córdoba) y algunos de mis compañeros (Ángel Castro, Francisco Gancedo y Javier Gómez) y otros colaboradores (el medallista Field Charles Fefferman) hicieron un importante avance. Probaron la existencia de otro tipo de singularidad para el caso de las olas. Bautizaron a esta singularidad como “splash”. Arremanguémonos y veamos un poco las matemáticas que hay debajo de todo esto…

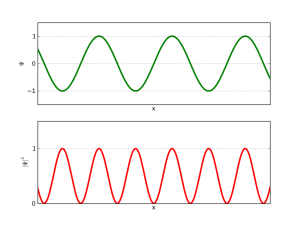
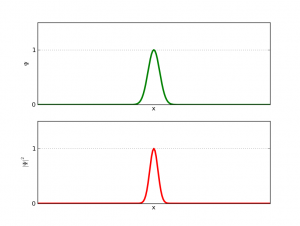
Consideremos una curva en el plano. Esta será nuestra ola inicial. La evolucion de esta ola viene dada por la evolución del fluido bajo ella. Se trata así de un problema de frontera libre, es decir, donde el propio dominio es una incógnita. Así tenemos que, bajo la ola, se verifican las ecuaciones de Euler incompresibles y que además el fluido es irrotacional. Sobre la curva suponemos que tenemos el vacío (esto es un buen modelo porque el agua tiene una densidad mucho mayor a la del aire). Lo que se sabía antes de los trabajos de Diego y compañía eran la existencia local de solución, es decir, que una ola “suave” sigue siendo una ola “suave” al menos un corto tiempo. Esta existencia local es cierta tanto en el caso donde se supone que la profundidad del mar es infinita como en el caso con un lecho marino predeterminado (son resultados de S. Wu y D. Lannes, respectivamente). También se sabe que si las olas “son muy planitas” la existencia es global, es decir, la ola existe para cualquier tiempo (resultados obtenidos independientemente por S. Wu y P. Germain, N. Masmoudi y J. Shatah).

[iframe: width=”400″ height=”320″ src=”http://www.youtube.com/embed/SdPI6yrjJoM” frameborder=”0″ allowfullscreen]

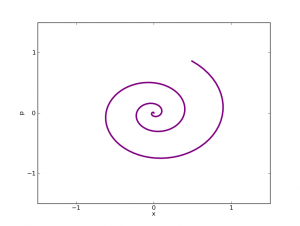
Los resultados con bandera española en este tema comienzan con un artículo (de A. Castro, D. Córdoba, C. Fefferman, F. Gancedo y M. López) donde se prueba que una ola que empieza siendo un grafo, es decir, se puede escribir como (x,f(x)), deja en un tiempo finito T de ser un grafo. De otra manera, la ola rompe. Matemáticamente esto es que la derivada espacial de la ola se hace infinita en algún punto. El resultado de hace unos días que he mencionado más arriba abunda más en esta línea. Lo que A. Castro, D. Córdoba, C. Fefferman, F. Gancedo y J. Gómez prueban es que existen olas que empiezan siendo curvas suaves y que en un tiempo finito se tocan. Es decir, se ha perdido la propiedad de ser una curva sin autointersecciones. Así es plausible el escenario de comenzar con un grafo, evolucionar hasta perder la propiedad de ser un grafo, es decir, la ola rompe, y, al continuar pasando el tiempo, la curva se acabe autointersecando. Esto es justamente lo que hemos visto en el primer video de esta entrada. Así que podemos concluir dos cosas: una es que algo tan cotidiando como una ola puede ser matemáticamente un problema muy difícil. La segunda cosa que podemos aprender es que nuestro modelo para la dinámica de fluidos funciona en el sentido de que recupera comportamientos reales observados en la naturaleza.

Antes de acabar quiero agradecer a mi compañero Javier Gómez que nos haya dejado el video de sus simulaciones.

—-Esta es nuestra contribución a la edición 2.5 del Carnaval de Matemáticas (http://carnavaldematematicas.bligoo.es/), que está siendo albergado por el blog Juegos Topológicos (http://topologia.wordpress.com/d).

Cuántica e incertidumbre (Parte I)

Posted on by
Reply
Hoy vamos a hablar, procurando no ser muy rigurosos (aparecen algunas fórmulas pero se pueden saltar), de por qué la mecánica cuántica es necesaria y del principio de incertidumbre de Heisenberg. La entrada la hemos escrito de manera conjunta Rafa y yo mismo.
Werner Heisenberg

Werner Heisenberg, uno de los padres de la Mecánica Cuántica

Principios de incertidumbre hay muchos, básicamente no es mas que una desigualdad de cierto tipo, donde un término controla a otro. En el caso concreto que nos atañe afirma que es imposible conocer con precisión la posición y la velocidad de una partícula cuántica (para fijar ideas un electrón). Los físicos (experimentales al menos) razonan diciendo que eso es porque para detectar un electrón hay que golpearlo con un fotón y entonces cambias su velocidad.
Esto nos deja con la duda: ¿habrá algún método que permita conocer las dos cosas?
La respuesta es que no. Y el motivo, enraizado en las matemáticas, tiene que ver con la transformada de Fourier. El ‘teorema’ aquí es que si tienes una función “grande” su transformada de Fourier es “pequeña” y viceversa (se puede intuir usando la desigualdad de Haussdorf-Young por ejemplo.). ¿Cómo afecta esto a nuestro electrón?. Los impacientes estarán pensando que se me está yendo la olla.
Pero comencemos aclarando por qué todas estas cosas tan raras de la cuántica son necesarias: supongamos que tenemos un átomo de hidrógeno (un electrón y un protón), y que tanto nuestro electrón como el núcleo del átomo se comportan como partículas clásicas. Entonces, al tener el núcleo carga eléctrica positiva y nuestro electrón carga eléctrica negativa deberían atraerse por la fuerza coulombiana entre ellos. Cuando un cuerpo con carga se acelera emite radiación electromagnética (véase la fórmula de Larmor [aquí inglés]) perdiendo así energía.
Trayectoria en espacio fásico

En una dimensión, la posición del electrón, x, oscilaría y caería hacia el origen de coordenadas. Su velocidad, p, también oscilaría y lo llevaría hacia el centro, radiando energía en el proceso.

Según este modelo el electrón se vería atraído irremisiblemente hacia el núcleo y acabaría chocando con éste. Pero esto implicaría ¡que no habría electrones!. En jerga científica diríamos que la materia no sería estable. Puesto que nosotros somos materia y estamos aquí las hipótesis de nuestro modelo no pueden ser correctas.
En otra entrada explicaremos la descripción de los estados en mecánica clásica y cuántica, pero permitidnos ahora que hagamos algunos supuestos. En la mecánica clásica la evolución de un sistema se describe como la trayectoria de un punto en el estado de fases. Sin embargo, en la mecánica cuántica esto no es posible, dado que el estado de un sistema solo puede venir dado como una “probabilidad”, de modo que no existe trayectoria de un solo punto que se adecue a la evolución temporal de un estado. Aquí, pues, la incógnita será una función (con argumentos en el espacio-tiempo y con valores en los complejos) \Psi (x,y,z,t) cuyo módulo al cuadrado (que es un número real) nos dará la densidad de probabilidad de que un sistema se encuentre en un cierto estado.
Esta función, que llamaremos “función de onda”,  evoluciona de acuerdo con la ecuación de Schrödinger. Esta es una ecuación en derivadas parciales (EDP) “cualitativamente” hiperbólica (ver la entrada anterior ). Para mayor simplicidad vamos a suponer aquí que no depende del tiempo, con lo que ahora nuestra ecuación de Schrödinger es elíptica y se puede escribir como la función que minimiza un funcional de acción (ya hablamos antes de este concepto)  J(\Psi)= \int |\nabla \Psi(x)|^2 dx +\int V(s)|\Psi(x)|^2 dx
Si utilizamos, como representación de la función de onda,  la base de POSICIONES, la densidad de probabilidad asociada a nuestra función de onda, \int_A |\Psi(x)|^2dx,  nos dará la probabilidad de que el sistema (en este caso, nuestro electrón) esté en una zona A del espacio.
Si nos interesa el MOMENTO (i.e. la velocidad), su función de onda es la transformada de Fourier de la función de onda de posiciones, \hat{\Psi}(p),  y esta es la madre del cordero.
En la mecánica clásica la posición y el momento eran independientes. Por eso, podríamos realizar medidas sobre una y otra cantidad sin afectar a la otra.
Ahora, no obstante, tenemos una ligadura: hay una relación que conecta la posición y el momento, y ha de cumplirse. Podemos, pues, escribir nuestro funcional en términos de las dos funciones de onda J(\Psi,\hat{\Psi})= \int |\hat{ \Psi}(p)|^2|p^2| dp +\int V(s)|\Psi(x)|^2 dx.
La formulación del principio de incertidumbre de Heisenberg es, pues, \int x^2|\Psi(x)|^2 dx \int p^2|\hat{\Psi}(p)|^2 dp=\int |\nabla_x \Psi(x)|^2 dx \int |\nabla_p \hat{\Psi}(p)|^2 dp\geq C donde C es cierta constante que podemos escribir explícitamente pero que hacerlo nos da una pereza superlativa por lo que lo dejamos ‘para el lector interesado’ ;). La constante es una ensalada de constante de Planck \hbar, \pi, algún dos… Puede escribirse también involucrando sólo una función de onda de la misma manera que se hace con el funcional.
Hemos dicho que \Psi(x,t) nos da una probabilidad, con función de densidad |\Psi(x,t)|^2dx. Así observamos que en realidad el término \int x^2|\Psi(x)|^2 dx es la varianza de nuestra variable aleatoria |\Psi(x,t)|^2 (que asumimos tiene media x=0, es decir, que nuestro electrón está más o menos rondando el origen de coordenadas espaciales).
Entonces si entendemos esas ‘normas’ de los gradientes como los “errores” (utilizaremos esta palabra aquí a modo explicativo, pero hay que ser cautos con la terminología), veremos que un error pequeño en alguna de nuestras mediciones, para fijar ideas, la posición, implica que el error del momento (es decir, de la velocidad) tiene que ser alto para que el producto sea mayor que una constante. Es más: cuanto mejor midamos una (menor error) mayor es el error de la otra. ¡Qué vida más dura la nuestra!
No he hablado nada claro en este último párrafo, y los exigentes se habrán quedado pensando que me explico muy mal (quizá tengan razón). Hemos calculado un par de ejemplos ilustrativos usando python. Hemos supuesto que es unidimensional y que nuestras funciones de onda toman valores en los reales y no en los complejos. No lo hacen, pero sed generosos con nosotros que esto es sólo una afición.
Supongamos que nuestra onda es como la de esta figura
Función de onda con momento definido: seno

Si la funcion de onda es como un seno, la longitud de onda (o el momento) está bien definida.

Entonces por la fórmula de De Broglie, que conecta la visión de partículas con la de ondas, tenemos una velocidad definida (con poco o ningún error), que depende de la longitud de onda (¡otra entrada por hacer!). Esto de nuevo enlaza con nuestra transformada de Fourier, dado que este tipo de transformadas nos llevan desde el espacio de posiciones al espacio de momentos. Sin embargo, no conocemos nada de la posición, pues la probabilidad no se decanta por ninguna zona en particular y salvo puntos donde nunca estarán los electrones por lo demás no podemos decir nada. (Para el lector interesado, decir que esta función de onda no está bien definida en el espacio de posiciones: no es normalizable)
Otro caso interesante es algo así como:
Función de onda de un paquete gaussiano

Un paquete gaussiano es una elección "popular" de función de onda porque tiene incertidumbre mínima

En esta segunda imagen tenemos una función tal que al hacer el cuadrado obtenemos una zona que acapara casi toda la probabilidad, un entorno del origen (como la vida misma, unos pocos acaparan casi toda la proba…, digo, billetes). Es decir, casi sin error podemos saber su posición; sin embargo, no podemos usar la fórmula de De Broglie para calcular su velocidad, pues ¿quién me dice su longitud de onda?…
Para ir concluyendo ¿cómo enlaza esto con los gradientes (es decir, las derivadas)?, observamos que una función como la de la figura 1 tiene un gradiente ‘pequeño’, mientras que una función cómo la de la figura 2 tiene un gradiente ‘grande’. Sólo hay que ver que ese pico tiene una derivada bien grande. Así tenemos que entender que los gradientes me dan una idea del error, pero cambiando la variable. Es decir, una gradiente alto en las x me dice un error grande en las p y un error pequeño en las x. Aunque no hemos hablado de ello, esto tiene que ver con la estructura geométrica de las ecuaciones del movimiento Hamiltonianas (ya llegará, ya llegará…).
Es sorprendente (pero usual) cómo la física a veces acaba teniendo que ver con ideas abstractas de las matemáticas (al revés también ocurre).
Hay más que contar, pero se está insinuando una entrada muy larga, así que en la segunda parte de esta entrada escribiremos más acerca de los desarrollos matemáticos de la Transformada de Fourier y de si se puede obtener alguna propiedad física desde las matemáticas.
=======================
Esta entrada es participante en la XVIII Edición del Carnaval de la Física, alojado por “La Aventura , en la mecánica cuántica esto no es posible, de la Ciencia“.

¿Qué es exactamente una EDO?

Posted on by
2

A lo largo de las entradas de esta bitácora han ido apareciendo conceptos relativamente avanzados (ecuaciones en derivadas parciales…) sin mencionar casi los conceptos previos (previos en el sentido pedagógico, porque cronológicamente surge todo al mismo tiempo) como pueden ser las ecuaciones diferenciales ordinarias.

Una ecuación diferencial ordinaria (EDO a partir de ahora) es una expresión que relaciona la derivada de la función incógnita con la propia función. Así el problema queda reducido a ver si podemos encontrar (o demostrar que existe) una función tal que se verifique una relación más o menos complicada entre ella y sus tasas de cambio.

Un ejemplo lo tenemos en la Ley de Malthus. Supongamos que tenemos un número de insectos f. El incremento del número de insectos evolucionará de manera proporcional a el mismo, o de otra manera, en ausencia de rivales o limitaciones propias del medio la cantidad de hijos que medran es proporcional al número de padres. Razonable, ¿verdad?. Así la EDO la podemos escribir como f'(t)=cf(t), f(0)=f_0.

Unos comentarios antes de seguir: el número de datos iniciales (como f(0)=f_0 en el ejemplo anterior) tiene que ser el mismo que el máximo número de derivadas presentes en la expresión. Así como la ecuación anterior tenía una derivada debíamos poner un dato inicial. En el ejemplo del oscilador armónico al tener la ecuación x''=\omega^2 x necesitamos dos datos iniciales, x(0)=x0 y x'(0)=v0. Supongamos que tenemos una EDO de segundo orden (es decir, con dos derivadas) como la del oscilador armónico, entonces la solución general se escribe como $latex f(t)= c_1 e^{omega t}+ c_2e^{-omega t}$, donde para c_i son dos constantes que se fijan usando los datos iniciales.  Es decir, el conjunto de soluciones de una EDO linear de segundo orden (sin usar los datos iniciales) es un espacio vectorial (gracias a la linearidad) de dimensión 2 (el número de derivadas). Esta es una diferencia fundamental (y poco conocida entre los físicos) con respecto a las EDPs, pues una EDP tiene un espacio de soluciones de dimensión infinita.

Parece claro que conseguir escribir la solución de una EDO de manera explícita, es decir, una fórmula cerrada, no va a ser fácil o siquiera posible en cuanto la EDO sea no-lineal, por ejemplo algo como f''(t)=f^2(t)f'(t). Nos interesa entonces saber que existe dicha solución, ser capaces de simularla con el ordenador y ser capaces de extraer propiedades cualitativas.

Para una EDO general, f'(t)=F(t,f(t)), la existencia se puede segurar si se dan unas propiedades en la expresión F(x,y), a saber, que sea derivable en la variable y.

Para aproximar la solución de la EDO f'=F(t,f(t)) f(t_0)=f_0 se tienen que aproximar unas integrales, f(t)=f_0+\int_0^t F(s,f(s))ds. Según el método que usemos tendremos una mejor o peor cota del error cometido. La manera típica, conocida como métodos Runge-Kutta, de hacerlo es considerar una serie de puntos entre dos nodos temporales y calcular el valor de la función F en esos puntos. Después hemos de sumar dichos valores con unos pesos. La teoría de los métodos Runge-Kutta es bien conocida y se puede encontrar en la red sin mucho problema (siempre que se hable un mínimo de inglés al menos). Aquí voy a colgar unos códigos hecho por mí:

function [u,t,h,totalt]=euler(F,t0,T,u0,N)
%funcion que aproxima con un metodo de Euler explicito la solucion de la edo
%u’=F(u,t) hasta tiempo T con N nodos temporales. u0 es el dato inicial.
%%Rafael Granero Belinchon
tic
h=(T-t0)/N;
t=[t0:h:T];
u=zeros(N+1,1);
u(1)=u0;
for i=2:N+1
u(i)=u(i-1)+feval(F,u(i-1),t(i-1))*h;
end
plot(t,u);
totalt=toc;

function [u,t,h,totalt]=rungekutta4(F,t0,T,u0,N)
%Funcion que aproxima con una RK4 la solucion de
%y’=F(y) y(t0)=u0 y tiempo final T. N da el numero
%de nodos temporales.
%%Rafael Granero Belinchon
tic
h=(T-t0)/N;
t=[t0:h:T];
u=zeros(N+1,1);
u(1)=u0;
for i=2:N+1
s1=feval(F,u(i-1),t(i-1));
s2=feval(F,u(i-1)+h*0.5*s1,t(i-1)+h*0.5);
s3=feval(F,u(i-1)+h*0.5*s2,t(i-1)+h*0.5);
s4=feval(F,u(i-1)+h*s3,t(i-1)+h);
u(i)=u(i-1)+(s1+2*s2+2*s3+s4)*h/6;
end
plot(t,u);
totalt=toc;

function [u,t,totalt]=rungepasovariable(F,t0,T,u0,N,tol)
%funcion que aproxima con un metodo de paso variable
%la solucion de la ecuacion diferencial y’=F(y) en [t0,T]
%con u0 como dato inicial una cantidad N de pasos temporales y una tolerancia tol.
%%Rafael Granero Belinchon
tic
t=[t0];
dt=(T-t0)/N;
u=[u0];
u1=u;
u2=u;
while t(end)<=T
fev=feval(F,u(end),t(end));
s=u(end)+0.5*dt*fev;
u2(end+1)=u(end)+feval(F,s,t(end)+0.5*dt)*dt;
u1(end+1)=u(end)+fev*dt;
err=abs(u2(end)-u1(end));
h=0.9*dt*sqrt(tol/err);
u(end+1)=u(end)+feval(F,s,t(end)+0.5*h)*h;
t(end+1)=t(end)+h;
dt=h;
end
totalt=toc;

Caminos aleatorios e imágenes

Posted on by
1

Esta es nuestra entrada para el Carnaval de Matemáticas 2.2 (alojado esta vez en Gaussianos).

Muchas veces se ha escrito sobre la relación entre los caminos aleatorios y la ecuación del calor, y quizá próximamente tratemos nosotros ese tema. Sin embargo hoy vamos a ver una aplicación poco conocida de esa relación. En esta entrada vamos a tratar brevemente una manera de emplear las matemáticas, y mas concretamente los caminos aleatorios o las trayectorias brownianas, para que un ordenador sepa qué imagen está ‘viendo’. Ahora que han puesto unos radares de tramo (que funcionan memorizando las matrículas de los coches y midiendo tiempos para calcular la velocidad media del tramo donde está el radar) en las carreteras españolas este problema tiene una clara aplicación práctica.

Desde hace unos años el tratamiento de imágenes usando ecuaciones en derivadas parciales es un área de investigación matemática floreciente. Normalmente tratan el problema de detectar los contornos de una imagen o de suavizarlos (de manera que veamos mejor la imagen). Nuestro problema es ligeramente distinto. Nosotros, dada una silueta (es decir un contorno cerrado y suave que encierra un área negra mientras que lo de fuera es blanco), tenemos que enseñar al ordenador a sacar propiedades de los contornos de manera que aprenda a distinguir entre las distintas siluetas.

La manera usual de extraer propiedades de una silueta es ‘medir’ y ‘clasificar’ los puntos del interior del contorno en función de su posición relativa a la curva que delimita la silueta (a partir de ahora la denotaremos S, mientras que el contorno será \partial S). Esto puede hacerse por ejemplo con la distancia mínima. Es decir, a cada punto interior se le asigna un valor que viene dado por la distancia mínima a \partial S. Se forma así lo que se llama una segmentación (se divide la silueta en partes) que no es muy regular (he apostado con David a que vosotros, los lectores, podéis encontrar un ejemplo muy rápido…). Para utilizar esta manera de relacionar puntos del interior con la frontera lo que se hace es resolver la ecuación eikonal con condiciones de borde Dirichlet sobre la silueta: es decir se resuelve |\nabla u|^2=1\;\;x\in S,\; u(x)=0\;\; x\in \partial S. Esta manera tiene ciertas desventajas, algunas matemáticamente obvias. Por ejemplo podemos convencernos rápidamente de que la ecuación anterior no tiene una única solución. En efecto, consideremos el problema en una dimensión: tenemos así a ecuación diferencial ordinaria |u'(x)|=1 en un intervalo acotado. Podemos construir infinitas soluciones, basta con ir construyendo triángulos con lados de pendiente 1 o -1. Podemos construirlos más grandes, más pequeños, unos pocos o muchos… Cada una de estas construcciones será una solución ‘débil’ (otro día hablaremos más de la soluciones débiles, hoy lo dejo caer sólo :P).

Así que si descartamos la aproximación anterior tenemos que proponer una nueva… para que no nos digan que hacemos críticas destructivas. Así que lo que hacemos (ver la referencia más abajo) es considerar un camino aleatorio, y más concretamente consideramos el tiempo medio, que denotamos por t que tarda una partícula que siga dicho camino aleatorio en golpear \partial S si inicialmente estaba en un punto x\in S. Cuando a cada x le asignamos este t tenemos una segmentación. ¿Qué ecuación diferencial cumple? En (1) la motivan razonando de la siguiente manera: sea t(x,y) el tiempo medio que emplean estas partículas en golpear el contorno del dominio saliendo desde el punto (x,y) (interno de la silueta S). Entonces si (x,y)\in \partial S se tiene que t(x,y)=0, si no, por ser las probabilidades uniformes se tiene que se puede calcular conociendo los valores de los puntos vecinos. Efectivamente, si estamos en un punto (x,y) y conocemos el valor de t en los puntos inmediatamente vecinos lo que podemos hacer es ‘gastar un movimiento’ en movernos a un punto vecino (siguiendo el camino aleatorio uniforme, lo que nos da una probabilidad 1/4 de elegir un determinado punto adyacente) y sumarle el tiempo medio que se emplea desde este nuevo punto. Por lo tanto se tiene que el valor es
t(x,y)=1+\frac{1}{4}\left(t(x+dx,y)+t(x-dx,y)+t(x,y+dx)+t(x,y-dx)\right).

Entonces observamos que la discretización del Laplaciano es
\Delta t(x,y)\approx\frac{t(x+dx,y)+t(x-dx,y)+t(x,y+dx)+t(x,y-dx)-4t(x,y)}{dx^2}, y por lo tanto la ecuación anterior es una versión discretizada de -\Delta t=\frac{4}{dx^2}.

Una manera rigurosa de obtener la misma conclusión es considerar la ecuación
\frac{1}{2}\Delta u=-1, con datos de borde Dirichlet homogéneos. Sea ahora \tau_{(x,y)}=\inf\{s:X_s(x,y)\in\partial S\}. Entonces se tiene
u(x,y)=E[\tau_{(x,y)}].

La idea de la demostración es aplicar la fórmula de It\^ o (ver (2) o (3)) al proceso $u(X_s)$, donde $X_s$ es un movimiento browniano, obteniendo la fórmula siguiente tras tomar esperanzas

E[u(X_{\tau_{(x,y)}})]-E[u(x,y)]=E\bigg{[}\int_0^{\tau_{(x,y)}}\Delta u(X_s)ds\bigg{]}.

Ahora usamos las condiciones de borde y la ecuación para obtener
0-u(x,y)=-E\bigg{[}\int_0^{\tau_{(x,y)}}1ds\bigg{]}=-E[\tau_{(x,y)}], concluyendo la demostración.

Una vez que tenemos t solución de la ecuación de Poisson anterior lo que hacemos es definir nuevas funciones \Phi(x)=u(x)+|\nabla u(x)|^2 y y \Psi(x)=-\nabla\cdot\bigg{(}\frac{\nabla u}{|\nabla u|}\bigg{)} (entre otras). La función Phi tiene ciertas propiedades que la hacen interesantes, pero para el tratamiento de imágenes lo más importante es que los valores altos de \Phi indican concavidades (allí el gradiente es grande) y que podemos utilizar el método del umbral para dividir nuestra forma en partes sin perder información. La función Psi (cuyo operador es el 1-Laplaciano) tiene la propiedad de que ciertos valores se alcanzan en zonas curvadas. Por lo tanto sirve para encontrar esquinas en nuestra forma. Los valores negativos de \Psi indican concavidades. Cuanto más negativo más ‘picuda’ es la concavidad. Al reves también funciona, los valores altos indican convexidades. Así extraemos información de la imagen y el ordenador puede discernir entre ellas.

Para el lector familiarizado con Matlab dejamos un código. Con estas funciones se puede experimentar un poquito lo que hemos estado diciendo.

function [img,img2,u,t,cnt]=imagessor(tol,itmax,image)
%this program use the sor method for solve the poisson equation in a silhouette
%tol is the tolerance
%itmax is the maximum number of iterations
%image is an png image.
%Rafael Granero Belinchon

tic
img=imread(image);
figure;imagesc(img);
input(‘Press any key’)
img=double(img);
[H,W]=size(img);
w= 2 / ( 1 + sin(pi/(H+1)) );%our overrelaxation parameter
for i=1:H
for j=1:W
img2(i,j)=abs(img(i,j)-255); %change white for black and viceversa
end
end
img2;
figure; imagesc(img2);
input(‘Press any key’)
clear i,j;
%now we start with the algorithm. Like maybe it will be difficult put the geometry of the silhouette
%we use the easy bounday conditions to treat all the image, but we only solve the poisson inside the silhouette.
%This maybe is not efficiently, but is easier.
u=img2;
v=u;
err=1;
cnt=0;
while((err>tol)&(cnt<=itmax))
for i=2:H-1
for j=2:W-1
if (img2(i,j)==0)

else
v(i,j)=u(i,j)+w*(v(i-1,j) + u(i+1,j) + v(i,j-1) + u(i,j+1) +1 – 4*u(i,j))/4;
E(i,j)=v(i,j)-u(i,j);
end
end
end
err=norm(E,inf);
cnt=cnt+1;
u=v;
end
u=flipud(u);
figure;imagesc(u);
mesh(u)
t=toc;

function [Phi,t]=phi(u,NGu)
%This program calculate the function phi=u+NGu^2
%NGu is the norm of the gradient of u
%Rafael Granero Belinchon

tic
[H,W]=size(NGu);
for i=1:H
for j=1:W
Phi(i,j)=u(i,j)+NGu(i,j)^2;
end
end
t=toc;

function [Psi,t]=psiimages(u,Gux,Guy,NGu)
%This program calculate the function psi=-div(gradient(u)/norm(gradient(u))
%NGu is the norm of the gradient of u
%Gux is the first component of the gradient,
%Guy is the second one
%Rafael Granero Belinchon

tic
[H,W]=size(NGu);
for i=2:H
for j=2:W
Psix(i,j)=((Gux(i,j)-Gux(i-1,j))*NGu(i,j)-Gux(i,j)*(NGu(i,j)-NGu(i-1,j)))/NGu(i,j)^2;
Psiy(i,j)=((Guy(i,j)-Guy(i,j-1))*NGu(i,j)-Guy(i,j)*(NGu(i,j)-NGu(i,j-1)))/NGu(i,j)^2;
Psi(i,j)=-Psix(i,j)-Psiy(i,j);
end
end
t=toc;

function [Gux,Guy,NGu,t]=gradient(u)
%This program calculate the gradient and its norm
%Gux is the first component of the gradient,
%Guy is the second one
%NGu is the norm of the gradient
%Rafael Granero Belinchon

tic
[H,W]=size(u);
for i=2:H
for j=2:W
Gux(i,j)=u(i,j)-u(i-1,j);
Guy(i,j)=u(i,j)-u(i,j-1);
NGu(i,j)=(Gux(i,j)^2+Guy(i,j)^2)^0.5;
end
end
t=toc;

(1) L.Gorelick, M.Galun, E.Sharon, R.Basri, A.Brandt, ‘Shape Representation and Classification Using the Poisson Equation’, IEEE transaction on pattern analysis and machine intelligence, 28 (2006), no.12, 1991-2004.

(2) H.Kunita, Stochastic differential equation and stochastic flows of diffeomorphism, Lecture Notes in Math. vol 1097, Springer, 1984.

(3) H.Kunita, Stochastic flows and stochastic differential equations, Cambridge studies in advanced mathematics, 1997.

Inferir la Ley: ¿es siquiera posible?

Posted on by
2

El Viernes pasado estuve en la conferencia “SERIES LÓGICAS Y CRÍMENES EN SERIE” de Guillermo Martínez, el autor de “Crímenes imperceptibles” (que es la novela en la que se basa la película “Los crímenes de Oxford”. La presentadora de la conferencia fue Rosa Montero y estaba organizada por el Instituto de Ciencas Matemáticas (que es donde trabajo).

La presentación del conferenciante no me gustó mucho. Creo que la señora Rosa Montero transmitió una serie de tópicos sobre los matemáticos que se pueden resumir en la siguiente frase, que cito textualmente,

“Tener un amigo matemático es como tener un amigo trapecista: exótico.”

La conferencia en sí no estuvo mal… No eran matemáticas y sospecho que este tipo de charlas divulgativas tienen un efecto contraproducente, pero Guillermo Martínez lo contó muy bien y ameno. En general pienso que este tipo de charlas hace que la gente culta de formación no-matemática piense que nosotros lo que hacemos es…mmm… ¿contar? ¿resolver problemas de lógica como los de los libros de pasatiempos? Y en una ausencia completa de humildad piensan que la matemática es algo completamente inútil. ¡Cómo no va a ser inútil resolver pasatiempos de manera profesional! Creo que toda conferencia divulgativa debería empezar indicando algo así:

“Señores, lo que van a ver aquí está muy alejado del campo en cuestión. Es algo divertido y fácil de entender, no como los problemas reales que tratamos de resolver.”

Vamos ahora al tema de la conferencia en cuestión: las series lógicas. Una serie lógica es una colección de símbolos o números finita y para la que se necesita continuación. Por ejemplo, 2,4,8,16… En la conferencia se nos habló de la falta de unicidad para la continuación. Es decir, que dada una serie la respuesta correcta no es única. En el ejemplo anterior todo el mundo diría que sigue el 32, pero 31 también es una respuesta correcta (se puede razonar, si alguien tiene interés que ponga su duda en los comentarios y la responderé).

Guillermo Martínez usó un argumento basado en interpolación para concluir que dada una colección finita de números hay una manera de razonar que permite continuar la serie con cualquier otro número. La idea es que dada la serie 2,4,8,16, la respuesta puede ser x para cualquier número. Eso es porque podemos construir un polinomio (que se llama polinomio interpolador de Lagrange) de manera que pase por los puntos (1,2), (2,4), (3,8) (4,16) y (5,x), por lo tanto dicho polinomio es una Ley que concuerda con los experimentos anteriores, pero entre las distintas “Leyes” difieren en el 5º experimento. Ludwig Josef Johann Wittgenstein ya habló de eso en su obra.

Así, dada una colección aparentemente aleatoria de números, podemos construir un polinomio interpolador que nos sirva de Ley y nos “explica” como “se han obtenido”. El tema de lo que significa “aleatorio” surge aquí, pues si dada una colección siempre podemos encontrar una Ley… ¿qué significa una colección de números aleatorios? Por ejemplo, en Matlab tenemos la función rand, que nos da un número entre 0 y 1 “aleatorio”. Claramente estos números no son aleatorios, los genera un ordenador usando una fórmula. Sin embargo usando los criterios existentes (que no nos dicen cuándo una secuencia es aleatoria sino cuándo una secuencia PASA POR aleatoria) son indistinguibles de números verdaderamente aleatorios (los que se sacasen con los ojos vendados de un bombo). Por lo tanto en la práctica nos sirven.

El problema de la inferencia de una Ley dado un número finito de experimentos es irresoluble, ya lo dijo Wittgenstein, sin embargo es lo que hace la física todos los días de manera más que aceptable. Basta con tener una Ley “dinámica”, me explico, si vale la usamos, cuando no valga la cambiamos por una que nos cumpla todos los nuevos experimentos y así vamos tirando para delante. Y he de decir que de manera más que satisfactoria. Por lo tanto, quiero desde aquí tranquilizar a todos los asistentes a la conferencia a los que vi visiblemente sorprendidos, casi en estado de shock. De acuerdo, no podemos saber si la Ley que usamos es la correcta, pero, mientras nos funcione bien ¿qué más nos da? Lo demás son pasatiempos.

De contar, las integrales y los carnavales (de matemáticas)

Posted on by
3

(Esta es una entrada par participar en el X Carnaval de Matemáticas (http://carnavaldematematicas.drupalgardens.com/) organizado por La Ciencia de la Mula Francis (o Francis (th)E mule Science’s News, http://francisthemulenews.wordpress.com/))

En esta entrada para nuestro blog (http://ambages.es/blog/) vamos a hablar de las posibles maneras de contar que se nos ocurren y sus aplicaciones a la integración.

Desde los primeros cursos en el Instituto nos hacen que aprendamos unas cuantas fórmulas para el cálculo de volúmenes y áreas de cuerpos o figuras más o menos “corrientes”, pirámides, conos, cuadrados, círculos… Más tarde, ya en Bachiller nos enseñan la genial herramienta que es la Integral de Riemann.

Este concepto es clave, por lo que vamos a gastar unas líneas recordándolo. Supongamos, por facilitar la exposición, que estamos calculando el área bajo una curva y=f(x). Además, f es una curva curvada, nada de una linea recta o una poligonal. Lo que pensamos es, bueno, como sabemos la fórmula del área del rectángulo, vamos a ‘tapar’ el área bajo la curva con rectangulitos de distintos tamaños. Hecho esto observamos que el área calculada y el área que queríamos calcular no coinciden… pero si lo hemos hecho bien estarán muy cerca, si bien la que queremos calcular será un poquito mayor. La idea es ahora tapar ‘un poquito más’ del área buscada, para tener la certeza de que el área bajo la curva está entre dos valores aproximados y que son explícitos. Una vez hecho esto podemos tomar cada vez un mayor número de rectangulos para que nuestra estimación del área sea más precisa. Además argumentamos que en el límite cuando el número de rectángulos se hace infinito las 3 áreas, la buscada, la encontrada ‘por debajo’ y la encontrada ‘por arriba’, coincidirán.

Observamos que esto es válido para las curvas y=f(x) ‘razonables’. Como esta entrada es divulgativa no vamos a entrar en más detalles, pero es un ejercicio divertido (y fácil) tratar de encontrar una función que no se pueda integrar en el sentido de Riemann.

¿Qué os parece?, el cálculo de áreas, un problema central en la historia de la humanidad ya que está ligado a los campos de cultivo y por lo tanto al yantar, resuelto sin fórmulas complicadas ni nada parecido. Es cosa simplemente de ‘ir tapando con rectángulos’.

De esto ya se dio cuenta el genial Arquímedes (el que gritó ¡Eureka! y salió corriendo de la bañera). Así en su ‘Sobre la cuadratura de la parábola’ para calcular el área encerrada por un segmento de parábola lo que hace es tapar dicha superficie con triángulos isósceles de manera que lo que queda fuera de estos triángulos vuelven a ser segmentos de parábola similares al primero y de esta manera recurrente, sumando las áreas d elos infinitos triángulos calcular la superficie encerrada por la parábola inicial. Me gustaría señalar que la serie dada por las áreas de los triángulos es una serie geométrica de razón 1/4 y que Arquímedes la sumó entera. Es la primera vez en la historia (al menos que yo sepa) que se suma COMPLETA una serie geométrica (que es quizá la más fácil de las series), pues si bien en los Elementos de Euclides se da una fórmula para calcular la n-ésima suma parcial para cualquier n esto no es lo mismo que sumar la serie completa, hay una sutil diferencia.

Hasta ahora hemos hablado de integrales, áreas… pero nada de contar como dijimos al principio. Ahora vamos a eso. Supongamos que somos pobres becarios de investigación (lo de pobre es en sentido literal), y que queremos contar nuestro escaso peculio. Tenemos así monedas de 2 euros, de un euro, de 10 céntimos… vamos, de todas las monedas que hay. Una manera de contarlas es ponerse pacientemente, ir una a una e ir sumando. Primero cogemos una de 1 euro, luego una de 2 euros, luego una de 5 céntimos… Eso es lo que hace la integral de Riemann.


Pero esta manera de hacerlo no es la única. También podemos agrupar las monedas según su valor y contar cuantas tenemos en cada grupo. Así juntamos y nos salen 3 monedas de 2 euros por un lado, 10 monedas de 5 céntimos por otro… Ahora sólo hemos de multiplicar el número de monedas por su valor y sumar los resultados para cada grupo. Esta idea, para el cálculo integral, se llama Integral de Lebesgue. Lo que se hace es tapar con rectángulos según la altura de la función. Así en la figura adjunta (sacada de la wikipedia) se ve en azul la manera de integrar de Riemann y en rojo la manera de integrar de Lebesgue. Parece una tontería sin consecuencias, pero tiene unas consecuencias teóricas y prácticas importantisimas, de manera que es la Integral que los matemáticos usamos normalmente. Sin embargo, como es una entrada divulgativa, y no una clase de teoría de la medida lo voy a dejar aquí.

Introducción al cálculo variacional en la física

Posted on by
2

Siempre me ha resultado curioso la facultad sorpresiva de la Naturaleza. Nos empeñamos en admirar lo compleja que es en cada detalle. Y después descubrimos que, si miramos desde el punto de vista adecuado, todo es simple. Los científicos nos inventamos leyes (de acuerdo con unas observaciones) para intentar comprender cómo funciona, y al final basta con unos pocos principios fundamentales para derivar el resto.

Al principio estas leyes suelen ser engorrosas, pues de manera experimental intentamos contrastar nuestras observaciones con funciones que se asemejen a nuestros resultados con el fin de poder predecir más fenomenología. Así le ocurrió a Kepler que, habiendo heredado los datos de Tycho Brahe y teniendo observaciones de altísima calidad, enunció las tres leyes que llevan su nombre. Estas leyes requirieron de mucho trabajo experimental y análisis de datos para ser obtenidas y son todo un triunfo de la ciencia. Sin embargo, como en todos los campos científicos, son solo una aproximación de la realidad e introducir perturbaciones (dadas por otros planetas) eran necesarias para poder reproducir con más detalle los resultados.

Más tarde, arduos razonamientos acerca de las observaciones suelen llevar a refinamientos de la teoría. De este modo, Newton propuso la “ley de la gravitación universal” que, aplicada a un sistema simple bajo ciertas suposiciones, ¡daba como resultado las leyes de Kepler!

En el ejemplo anterior, afortunado donde los haya, no he querido entrar en las teorías anteriores de epiciclos y deferentes. Estas “teorías” se ajustaban muy bien a los datos experimentales y por eso tardaron tanto en ser desbancadas. Sin embargo, recientemente se ha demostrado que dado un número suficiente de epiciclos y deferentes, se puede reproducir cualquier órbita, pero esto no nos interesa… lo que queremos es saber cómo son las cosas y, en general, predecir el comportamiento de los sistemas de acuerdo con nuestro conocimiento: si nuestro método puede dar como pronóstico cualquier cosa , la realidad deja de tener sentido y pasa a ser un caso particular, en vez de ser el sujeto central de lo que nos atañe.

Por eso es tan importante la simplicidad. El objetivo de todo científico es poder hacer prediciones sobre el comportamiento de la realidad; si está descrito de manera muy compleja es posible que no estemos teniendo en cuenta los parámetros y simplificaciones adecuados para nuestro sistema en cuestión.

Supongo que algo así deberían tener en la mente los científicos y matemáticos de los siglos XVIII y XIX cuando fundaron lo que se denominó “mecánica analítica”.  Para ello, utilizaron el metafísico “principio de mínima acción” que plantea, en palabras de Maupertuis [1] que

“…la Naturaleza siempre actúa  de la manera más simple posible para producir sus efectos.”

Y… ¿para qué sirve este principio?  Voy a ilustrarlo con un ejemplo de mecánica clásica.  Queremos saber qué camino tomará un cuerpo en una cierta situación. Imaginemos que tenemos una cantidad (un funcional, matemáticamente hablando), a la que llamaremos acción, que depende del “camino” que ese cuerpo toma en su movimiento. Esa acción puede ser calculada para cada cualquier camino siempre y cuando tenga una cierta regularidad.  Pues bien, el camino real, el que tomará el cuerpo y que podrá ser predicho, es aquel que hace de la acción un mínimo (más rigurosamente, un valor estacionario).  Esto es “fácil” de entender:

Si calculamos la acción para todos los caminos, escogemos el camino que tiene la acción más pequeña, esa trayectoria es nuestra solución.

Simple, ¿no?

Muestra del principio de mínima acción en algunos posibles caminos

Si a cada posible trayectoria de un cuerpo entre los puntos inicial y final de su trayectoria se le asigna una acción S, la trayectoria real será aquella que tenga la acción menor. Aquí, la segunda trayectoria 2 será la real, por tener la acción menor al resto.

Pensémoslo por un segundo… ¿no es cierto que el número de caminos posibles es infinito? ¡¿Tenemos que calcular la acción para todos los posibles caminos?!

La respuesta es “no”.  Hete aquí la belleza de la Naturaleza y del ingenio humano. Matemáticamente es un poco engorroso de explicar, y se necesita alguna fórmula, de modo que  dejaré tan engorrosa tarea a Rafa, más versado que yo en estos temas.

Uno de los trabajos de la física es averigüar cuál es la definición correcta de acción que nos da resultados que se correspondan con el comportamiento de la Naturaleza.

Por mi parte, y como estaba planeado, escribiré sobre las dos principales ramas de esta teoría en la física, el método Lagrangiano y Hamiltoniano, utilizando como guía el oscilador armónico. De este modo, comprenderemos un poco mejor las ventajas y desventajas de este método en comparación con la mecánica vectorial de Newton (de la que ya hablamos aquí)

Por último, una reflexión:

Simplicidad no implica que vaya a ser fácil obtener un resultado correcto. Simplicidad implica que puedes contárselo a tu abuela (de una manera más o menos burda).

En estas lineas, Euler dejó escrito [2]:

“Comparados con los métodos de la mecánica tradicional, puede ser que el movimiento sea más dificil de calcular utilizando nuestro nuevo método; sin embargo, parece más fácil de comprender desde primeros principios.”


Referencias:

[1] Maupertuis, Accord de différentes loix de la nature qui avoient jusqu’ici paru incompatibles (1744) (Traducción inglesa, original en francés) Nótese que aplica su sistema a la óptica, como lo hizo antes Fermat.

[2] Euler, Metodus inveniendi. Additamentum II (1744) (traducción inglesa)

[3] Cornelius Lanczos. The variational principles of mechanics (1949)

(Esta entrada es una contribución al XV Carnaval de la Física alojado por Curiosidades de la Microbiología)

El oscilador armónico – Parte I

Posted on by
3

Hola a todos.
Esta entrada es mi primera contribución al blog, y siendo físico me gustaría comenzar con el que es el ladrillo de la física: el oscilador armónico.
El nombre, que nos da una idea de a qué nos estamos enfrentando, indica el movimiento de algo que se repite en el espacio y en el tiempo. Matemáticamente, siendo más estrictos, un movimiento armónico sería el descrito por una función “seno” o “coseno” . La palabra “armónico”, procedente del griego, nos da la idea de una conveniente proporcion y correspondencia entre unas y otras cosas. El concepto aparece en música, como la unión de sonidos acordes, y Kepler (amante de la música y con su mente puesta en ella) lo utilizaba como expresión de belleza y unión entre las matemáticas y el movimiento celeste. [Vease “La armonía de los mundos“] Continue reading →

¿Podemos ir hacia atrás (matemáticamente) en el tiempo?

Posted on by
2

Me comentó David que sería interesante que explicase un poquito de lo que significa la reversibilidad temporal desde el punto de vista de las ecuaciones en derivadas parciales (EDPs de ahora en adelante). Es decir, sin mencionar nada de entropías. Este es un tema muy interesante e importante aunque a primera vista parezca una tontería. Lo hemos puesto como una serie de dos entradas. La primera (esta que estás leyendo) presentará las EDPs más fáciles y estudiará sus propiedades de cara a la reversibilidad temporal. En la segunda veremos la derivación de unos modelos más complicados y trataremos de entender dónde aparece la irreversibilidad temporal. Lo cierto es que en cierto modo es llamativo, pues las leyes de Newton son reversibles en tiempo y muchas (casi todas) de las ecuaciones de las que hablaremos surgen de ellas.

Viendo qué ocurre:
Para entender qué quiere decir y qué implica la reversibilidad (o irreversibilidad) temporal hemos de comprender primero los ejemplos más básicos de EDPs. Como dato para los técnicos supondré que todos los problemas están puestos para (t,x)\in [0,T]\times\mathbb{R}. Inmerso en el texto hay imágenes .jpg, imágenes animadas .gif (pinchad en ellas para que empiecen a moverse) y código Matlab (¡usadlo si podéis!).

La ecuación del transporte:

Comenzaremos con la ecuación del transporte unidimensional con coeficientes constantes. Esta es la EDP más sencilla que podemos poner.

\partial_t u + c \partial_x u=0, u(0,x)=f(x).

Supondremos que f es una función derivable con derivada continua una vez. La solución de esta ecuación es u(t,x)=f(x-ct) (¡comprobadlo!). Esta ecuación se llama ‘del transporte’ porque lo que hace es eso ‘mueve’ nuestra distribución inicial f. Si queremos cambiar el sentido del tiempo hemos de hacer el cambio t por -t. Entonces la nueva ecuación es

-\partial_t u + c \partial_x u=0, u(0,x)=f(x).

Observamos que el cambiar el tiempo de sentido es equivalente a cambiar el signo de c. Si utilizamos el código que propongo con varios valores de c observamos que este parámetro es una velocidad. Por lo tanto, parece natural que cambiar el sentido del tiempo cambie el sentido del movimiento. Es decir, que si para c>0 íbamos a la derecha, para tiempos negativos (o equivalentemente -c) tenemos que ir a la izquierda. Concluímos así que la ecuación del transporte es reversible en tiempo y que la reversibilidad es muy natural si partimos del proceso físico que se modela con esta ecuación.


Otra consecuencia, ésta mucho más sutil, de la reversibilidad temporal es que nuestra solución NUNCA va a ser mejor que nuestro dato inicial f. Esto es obvio en este caso porque tenemos una solución explícita, pero es cierto en general. Si u tuviese más derivadas que f entonces dando la vuelta al tiempo tendríamos una contradicción.

function [u,x,t]=transporte(dx,dt,f,c)
%%
%Funcion que me aproxima la solucion exacta (conocida) de la
%ecuacion del transporte u_t+cu_x=0 con dato inicial
% u(0,x)=f(x), paso espacial dx y paso temporal dt.
%f sera una funcion
% Rafael Granero Belinchon
%%

%Definicion de parametros:
T=10; %El tiempo final
t=0:dt:T; %el vector de tiempos
x=-pi:dx:pi; %el vector de espacio donde queremos
%nuestra aproximacion. No necesitamos condiciones de borde ¿por que?
u=zeros(length(x),length(t));
F=feval(f,x);

%Calculo de la solucion:
%La solucion del problema anterior es u(x,t)=f(x-ct)
u(:,1)=F;
for j=2:length(t)
u(:,j)=feval(f,x-c*t(j));
plot(x,u(:,j-1));%Representacion de los resultados
drawnow
end

function f=prueba(x)
f=sin(x);


La ecuación de ondas:

La siguiente ecuación es el paradigma de ecuación hiperbólica. Me refiero a la ecuación de ondas. Viendo el nombre está claro qué proceso físico quiere describir ¿no?.

Esta ecuación se escribe

\partial_t ^2 u= c^2\partial_x^2 u, u(0,x)=f(x), \partial _t(0,x)=g(x).

Visualmente parece mucho más complicada que la ecuación del transporte… sin embargo en realidad es igual (al menos en un cierto sentido). Vamos a escribirla como un sistema. Para ello definimos el sistema

\partial_t u=c\partial_x v, \partial_t v=c\partial_x u.

Si ahora derivamos en tiempo la ecuación para \partial_t u y utilizamos la segunda ecuación obtenemos

\partial_t^2 u=c\partial_x \partial_tv=c^2\partial_x ^2 u.

Es decir, que la ecuación de ondas no es más que dos transportes acoplados. Sin embargo todavía podemos hacerlo mejor. Podemos darnos cuenta de que el operador diferencial se puede escribir como

\partial_t^2-c^2\partial_x^2=(\partial_t + c\partial_x)(\partial_t-c\partial x),

y por lo tanto si tenemos u=u_1+u_2 con

\partial_t u_1 + c\partial_x u_1=0; \partial_t u_2 - c\partial_x u_2=0

tenemos una solución de la ecuación original. Concluímos que, como la ecuación del transporte era reversible, la ecuación de ondas, que se puede escribir como un par de ecuaciones del transporte debe ser reversible también.

La ecuación del calor:

Esta ecuación es parabólica. Se escribe

\partial_t u= \partial_x^2 u, u(0,x)=f(x).

Visualmente parece estar a medio camino entre la ecuación del transporte y la ecuación de ondas, sin embargo su comportamiento en radicalmente distinto. Para convencernos de ello podemos ‘jugar’ un poco con el código Matlab que adjunto. Los datos iniciales por defecto son los mismos, pero os animo a cambiarlos.

function [u,x,t,mx]=heatff(N,dt,K)
%%
%Funcion que me aproxima la solucion de la
%ecuacion del calor con dato inicial seno
%con condiciones periodicas (para usar FFT)
%N es el numero de nodos espaciales que se quieren
%usar. dt es el paso temporal que se quiere.
%K es la constante de difusion.
%Devuelve el espacio, el tiempo, la aproximacion de
%la solucion y el maximo de dicha solucion en cada tiempo
%Rafael Granero Belinchon
%%
T=5;%Tiempo final
dx=2*pi/(N-1);
x=-pi:dx:pi;%Espacio
t=0:dt:T;%Tiempo
uo=sin(x);%dato inicial
for k=1:N/2 %Operador laplaciano en espacio de fourier
L(k)=(k-1)*(k-1);
L(k+N/2)=(N/2-k+1)*(N/2-k+1);
end
L=K*L;
u(:,1)=uo’;
mx(1)=max(uo);
for l=1:length(t)
u(:,l+1)=ifft(exp(-L*dt*l).*fft(uo))’;%solucion
mx(l+1)=max(u(:,l+1));%Evolucion del maximo
plot(x,u(:,l));axis([-pi,pi,-1,1]);%Representacion de los resultados
drawnow
end
end

Para estudiar esta ecuación vamos a utilizar la transformada de Fourier. Para la transformada de Fourier de u(x) usaremos la notación \hat{u}(k). Así si transformamos la ecuación en espacio obtenemos las ecuaciones diferenciales ordinarias (EDOs a partir de ahora) indexadas en la longitud de onda k siguientes

\frac{d}{dt}\hat{u}(t,k)=-k^2\hat{u}(t,k), \hat{u}(0,k)=\hat{f}(k).

Esta ecuación la podemos resolver explícitamente

\hat{u}(t,k)=e^{-k^2t}\hat{f}(k).

Observemos ahora qué quiere decir el cambio del sentido del tiempo. De nuevo hagamos el cambio t por -t. La ecuación nos queda

\partial_t u= -\partial_x^2 u, u(0,x)=f(x).

No se ve nada claro, sin embargo, si buscamos los efectos del cambio en la solución explícita tenemos

\hat{u}(t,k)=e^{k^2t}\hat{f}(k),

de manera que cuando invirtamos la transformada de Fourier estamos calculando una convolución con una función que no está acotada, ni tiene ninguna potencia integrable… Vamos, que nuestra solución (que existe explícitamente) no está en ningún espacio razonable ni con propiedades físicas razonables. Por ejemplo, si u es la temperatura, entonces su integral (que es el calor) debe ser finita. Pues si damos la vuelta al tiempo obtenemos calor infinito para cualquier tiempo. Concluímos que la ecuación del calor NO es reversible en tiempo.

Una propiedad que a veces se da en las ecuaciones irreversibles y que es bien interesante es el ‘efecto regularizante’. Es decir, tu dato inicial f es continuo (por ejemplo), pero tu solución u es infinitamente derivable para todo tiempo (positivo). Como ya hemos mencionado antes, este comportamiento difiere del de las ecuaciones hiperbólicas usuales. La prueba de esto se puede hacer sin más que multiplicar por u e integrar por partes en espacio (¡comprobadlo!). Después basta observar que la ecuación es invariante por derivación tanto en tiempo como en espacio (¡Concluid el argumento!).

Vistos estos 3 ejemplos parece que hay una relación entre la ‘simetría’ del problema y su reversibilidad temporal. Quiero decir que, al menos de momento, las ecuaciones que tienen el mismo número de derivadas temporales que espaciales han resultado ser reversibles, mientras que las que no las tienen son irreversibles.

Otra cosa que se nos puede ocurrir es que las ecuaciones reversibles sean las que ‘no tiendan a nada’. Así vemos que la ecuación del calor tiende a ser idénticamente cero (necesita tiempo infinto para llegar a serlo) mientras que la ecuación del transporte sólo se movía por el espacio.

Veamos otro ejemplo:

La ecuación de Schrödinger:

Esta ecuación, clave en mecánica cuántica, se escribe

\partial _t u= i\partial_x^2 u, u(0,x)=f(x).

Si repetimos el análisis que hicimos para la ecuación del calor obtenemos que la solución es

\hat{u}(t,k)=e^{-ik^2t}\hat{f}(k),

que tiene un comportamiento oscilatorio. Por lo tanto, pese a tener una derivada en tiempo y dos en espacio se parece más a una ecuación de ondas que a una ecuación del calor. Observamos que el hecho de que aparezca la unidad imaginaria hace que u no sea real, sino compleja. Por lo tanto tiene una función conjugada. Si ahora cambiamos el sentido del tiempo observamos que para la función conjugada \bar{u} la ecuación es la misma. Por lo tanto si u es nuestra solución con el tiempo hacia delante, \bar{u} es una solución con el tiempo hacia atrás. Por lo tanto la ecuación de Schrödinger es reversible. Este ejemplo desmonta la hipótesis de que als reversibles debían tener el mismo número de derivadas en espacio y en tiempo.

function [u,x,t,L2,mx]=schrodinger(N,dt)
%%
%Funcion que me aproxima la solucion de la
%ecuacion de schrodinger con dato inicial seno
%con condiciones periodicas (para usar FFT)
%N es el numero de nodos espaciales que se quieren
%usar. dt es el paso temporal que se quiere.
%Devuelve el espacio, el tiempo, la aproximacion de
%la solucion, la norma L^2 de dicha solucion en cada tiempo
%y el maximo de la solucion en todo tiempo.
%Rafael Granero Belinchon
%%
T=5;%Tiempo final
dx=2*pi/(N-1);
x=-pi:dx:pi;%Espacio
t=0:dt:T;%Tiempo
uo=sin(x);%dato inicial
for k=1:N/2 %Operador laplaciano en espacio de fourier
L(k)=(k-1)*(k-1);
L(k+N/2)=(N/2-k+1)*(N/2-k+1);
end
L=i*L;
u(:,1)=uo’;
L2(1)=norm(uo)*dx;
mx(1)=max(abs (uo));
for l=1:length(t)
u(:,l+1)=ifft(exp(-L*dt*l).*fft(uo))’;%solucion
L2(l+1)=norm(u(:,l+1))*dx;%Evolucion de la norma L^2
mx(l+1)=max(abs(u(:,l+1)));%Evolución del máximo
plot(x,real(u(:,l)));axis([-pi,pi,-1,1]);%Representacion de los resultados
drawnow
end
end

Como dato anécdotico de esta ecuación hacemos notar que no puede reflejar efectos relativistas (¿por qué?).

En la próxima entrada, enlazando con esta, trataré la derivación desde la mecánica hamiltoniana de los modelos que se utilizan en mecánica de fluidos y trataré de explicar dónde aparece la irreversibilidad en el proceso. Sin embargo, esto es algo que no está ‘completamente entendido’ todavía.

La teoría del caos y el efecto mariposa

Posted on by
Reply

Para empezar sólo la voy a llamar teoría del caos en el título. Era para captar al atención, y este nombre lo consigue.  Es mejor decirle ‘de los sistemas dinámicos’ o algo así. Por desgracia, la fama de todo esto ha hecho que se encuentre de todo en internet. Por ejemplo hoy he visto una página donde se afirmaba que el efecto mariposa era los efectos de… ¡viajar en el tiempo! Impresionante. Y es que aficionarse a la ciencia está bien, pero sin perder el norte.

Por el nombre (caos) hay gente que piensa que un comportamiento caótico es aleatorio e impredecible. Vamos, un cisco bueno. Lo cierto es que lo primero es falso y lo segundo, como casi siempre, es ‘depende’.

El caos es ‘determinista‘, que quiere decir que dado un estado inicial, el comportamiento a largo plazo está determinado sin error posible y es único. Esto es, que está ‘determinado’ por el estado inicial. Consideremos un sistema discreto, es decir, una ley de recurrencia, por ejemplo la también famosa ley de Fibonacci, pero sin estados iniciales. Entonces la dinámica (la ley que sigue el sistema) es f_n=f_{n-1}+f_{n-2} Dados dos estados iniciales, por ejemplo 1,1 conocemos todos los valores de f. Además, si realizamos el experimento dos veces con los mismos valores iniciales los resultados serán idénticos. Eso quiere decir determinista.

Diferentes son los sistemas probabilistas. En estos sistemas hay un componente azaroso que impide conocer el largo plazo. Pero lo que de verdad los caracteriza es que para el mismo dato inicial podemos obtener resultados de los experimentos completamente distintos. Por ejemplo (muy poco válido como veremos ahora), una moneda. Consideramos el experimento tirar una vez la moneda. A mismas condiciones unas veces saldrá cara y otras cruz. Digo que es un mal ejemplo, porque este modelo es probabilista sólo por nuestro desconocimiento, pues si conociésemos la dirección y la fuerza exactas del lanzamiento sabríamos si saldrá cara o cruz. La gravedad es determinista. Esto nos podría llevar a pensar hasta que punto existe el azar, o si puede ser la probabilidad sólo una herramienta útil dada nuestra ignoracia de la realidad completa. Pensar en un mundo completamente determinista ya lo hizo Laplace. Y tiene una frase famosa por ello.

Ya hemos entendido la palabra determinista (si no es así tenéis que releerlo). Veamos el ‘depende’.

Es aquí donde entra el ‘efecto mariposa‘, que es el nombre que le puso Edward Lorenz a la sensibilidad a los datos iniciales. ¿A que es exótico?. Creo que su idea era atraer la atención hacia su conferencia. El efecto mariposa viene a decir que cualquier cambio minúsculo acaba teniendo repercusiones enormes, y por lo tanto nuestra aproximación (predicción) será una chapuza completa. O exóticamente

Si una mariposa batiese sus alas en Pekín provocaría un tornado en Texas un mes siguiente.

O algo parecido. Bueno, no matéis a todas las mariposas para evitar los tornados. No hay que cogerlo tan literal. En realidad hay que hacer una interpretación de casi todo. Las mariposas no provocan tornados. Los tornados surgen de un conjunto de factores que los hacen posibles, esto es, todas las mariposas del mundo, nuestros aviones, nosotros corriendo, la humedad en mi pueblo… Ahora, si pudiesemos tener dos planetas Tierra, con exactamente las mismas condiciones salvo una mariposa, entonces los climas serían distintos. ¿En qué sentido (ahora viene el depende)?. Bueno, no distintos en el sentido de que en Valencia helase por las noches. Llamemos a este tipo de cambios bruscos cambios de tipo 1. No, serían cambios en el orden y en el tiempo (tiempo-temporal, no tiempo-clima). Por ejemplo, un tornado que apareciese en un planeta el día 1 de Julio en el otro no aparecería y aparecería uno el 18 de Agosto. O una tormenta en mi pueblo no caería, caería en Albaladejo. Estos son los cambios de tipo 2.

Los cambios de tipo 1 son cambios bruscos que no quiere nadie. Estos cambios van asociados a cambios muy profundos en el sistema. Ahora tengo que ponerme técnico, lo siento. En un sistema dinámico, hay asociado un espacio de fases, que es un sitio donde viven las características del sistema. En este lugar de posiciones y velocidades (si es físico el sistema) o en el caso del clima de humedades y temperaturas, existen ‘cosas’ que atraen. Además son cosas raras normalmente en los casos caóticos. De hecho son fractales. Como no tenían muchas ganas de buscar un nombre exótico los llamaron ‘atractores extraños’. Posee la virtud de la simpleza. Los comportamientos del sistema cambian bruscamente entre unos atractores y otros (el mismo sistema puede tener varios al variar los parámetros). Es decir, para seguir con el ejemplo del clima, tenemos nuestro porcentaje de CO2 en la atmósfera en un nivel x. Nuestro sistema entonces tiene x como un parámetro. Si aumenta el porcentaje, digamos a 2x entonces nuestro sistema cambia de parámetro, pudiéndose producir un cambio de atractor, con el consiguiente nevazo en la Malvarrosa. Podemos ver esto del plano de fases y los atractores como un par de platos hondos y una aceituna, tenemos los platos juntos de manera que la aceituna reposa en el borde de ellos. La aceituna caerá rodando a uno de ellos. Los platos son los atractores, el conjunto de los dos es el espacio de fases y nuestra aceituna es el estado del sistema.

Dicho esto, está claro que hay que evitar los cambios de tipo 1. Los de tipo 2 son mejores en general.

Resumiendo, si tenemos un estado inicial, este nos viene dado por un conjunto de mediciones que hemos hecho. Estas mediciones no tienen (ni pueden) tener una precisión infinita (en cuyo caso el estado del sistema estaría determinado siempre) por lo que aparecen pequeños errores entre nuestro estado inicial para realizar los cálculos y la predicción y el verdadero estado inicial. Es decir, en nuestro espacio de fases hay dos puntos distintos, el de las medidas y el real. Al ser el comportamiento caótico, al avanzar el tiempo las curvas que tracen estos puntos se separarán. Y consecuentemente nuestra predicción a largo tiempo fallará.

Concluyendo, el ‘depende’ significa que podemos predecir el corto (quizá muy corto) plazo con poco error y podemos predecir si habrá cambio de atractor o no. Esto es comparable a decir que en Cuenca en Julio hará calor pero no poder decir habrá 36º C a las 15 de la tarde del día 2 de Julio. Decir que hará calor es decir el atractor, decir la temperatura exacta a la hora cabal es una predicción a largo plazo.

El comportamiento caótico existe, además es muy común. Aparece en todas las ramas del saber, física, biología medicina… Necesita algunas cosas para que se pueda dar. El sistema de ecuaciones diferenciales ha de ser no lineal y tener una dimensión mayor que dos. Pero esto no es nada raro en la cruda realidad fuera de las ‘oscilaciones pequeñas’ y cosas por el estilo.

He hecho un programita en Matlab para ver la sensibilidad a los datos iniciales:

function [x1,y1,z1,Y1,x2,y2,z2,Y2]=caoslogistica
%Este codigo estudia varios casos de 2 sistemas dinamicos discretos
%que conducen a un comportamiento caotico para ciertos valores
%de un parametro. Asi mismo dibuja unos diagramas de bifurcacion.
%Para el primer caso se puede poner k=4 para ver el comportamiento
%caotico. Para el segundo se puede poner k=1.6.
%Rafael Granero Belinchon.

disp(‘Comenzamos con el sistema dinamico Xn+1=k1Xn(1-Xn)’)
disp(‘—Primer Experimento:—‘)
k1=input(‘Dame una constante entre 0 y 4:’);
x0=input(‘Dame un valor inicial entre 0 y 1:’);
x1(1)=x0;
for i=1:100
x1(i+1)=k1*x1(i)*(1-x1(i));
end
disp(‘—Segundo Experimento:—‘)
k2=input(‘Dame una constante entre 0 y 4:’);
y0=input(‘Dame un valor inicial entre 0 y 1:’);
y1(1)=y0;
for i=1:100
y1(i+1)=k2*y1(i)*(1-y1(i));
end
disp(‘—Tercer Experimento:—‘)
k3=input(‘Dame una constante entre 0 y 4:’);
z0=input(‘Dame un valor inicial entre 0 y 1:’);
z1(1)=z0;
for i=1:100
z1(i+1)=k3*z1(i)*(1-z1(i));
end
subplot(4,1,1)
plot(x1);title(‘Primer experimento’);
subplot(4,1,2)
plot(y1);title(‘Segundo experimento’);
subplot(4,1,3)
plot(z1);title(‘Tercer experimento’);
subplot(4,1,4)
plot(z1,’r’);
hold on
plot(x1);
hold on
plot(y1,’k’);title(‘Todos juntos’);
hold off
a=input(‘Presiona cualquier tecla para continuar:’);
clear a;
disp(‘Comenzamos con el sistema dinamico Xn+1=k1Xn^2-1’)
disp(‘—Primer Experimento:—‘)
k1=input(‘Dame una constante entre 0 y 4:’);
x0=input(‘Dame un valor inicial entre 0 y 1:’);
x2(1)=x0;
for i=1:100
x2(i+1)=k1*x2(i)^2-1;
end
disp(‘—Segundo Experimento:—‘)
k2=input(‘Dame una constante entre 0 y 4:’);
y0=input(‘Dame un valor inicial entre 0 y 1:’);
y2(1)=y0;
for i=1:100
y2(i+1)=k2*y2(i)^2-1;
end
disp(‘—Tercer Experimento:—‘)
k3=input(‘Dame una constante entre 0 y 4:’);
z0=input(‘Dame un valor inicial entre 0 y 1:’);
z2(1)=z0;
for i=1:100
z2(i+1)=k3*z2(i)^2-1;
end
figure
subplot(4,1,1)
plot(x2);title(‘Primer experimento’);
subplot(4,1,2)
plot(y2);title(‘Segundo experimento’);
subplot(4,1,3)
plot(z2);title(‘Tercer experimento’);
subplot(4,1,4)
plot(z2,’r’);
hold on
plot(x2);
hold on
plot(y2,’k’);title(‘Todos juntos’);
hold off
a=input(‘Presiona cualquier tecla para continuar:’);
clear a;
disp(‘Vamos a dibujar ahora un diagrama de bifurcacion para el primer sistema’)
K=0:0.01:4;
X=zeros(length(K),5000);;
X(:,1)=0.3;
for j=1:length(K);
for i=1:5000
X(j,i+1)=K(j)*X(j,i)*(1-X(j,i));
end
end
Y1=X(:,4000:end);
figure
plot(Y1);title(‘Diagrama de bifurcacion para el primer sistema’)
a=input(‘Presiona cualquier tecla para continuar:’);
clear a;
disp(‘Vamos a dibujar ahora un diagrama de bifurcacion para el segundo sistema’)
K=0:0.01:4;
X=zeros(length(K),5000);
X(:,1)=0.3;
for j=1:length(K);
for i=1:5000
X(j,i+1)=K(j)*X(j,i)^2-1;
end
end
Y2=X(:,4000:end);
figure
plot(Y2);title(‘Diagrama de bifurcacion para el segundo sistema’)

Primer experimento (k=4)

La diferencia entre los datos iniciales es de 0.01 entre el de arriba y el segundo y de 0.001 entre el primero y el tercero. Como se puede ver en la gráfica de abajo, las trayectorias se separan más o menos por llegado un tiempo, pero al principio iban bien juntitas. Además podemos ver que todas estan en el mismo atractor. Eso se ve por los ‘patrones’ característicos que tienden a producirse. Me refiero a las oscilaciones grandes seguidas de varias muy pequeñas.  Esto se entiende fácil si se imagina uno nuestro estado del sistema como una mosca cansina. Estará dando vueltas a tu alrededor, quizá de forma complicada, pero antes o despues va a volver a pasar por tu oreja, quizá no como la vez anterior, pero muy cerca. Eso es lo que produce estos patrones. Que nuestro estado pasa cerca de una cierta parte del atractor.

Segundo experimento (k=1.6)

Arriba se muestran los resultados de ejecutar el código poniendo k=4 para el primer sistema y k=1.6 para el segundo. Veamos cómo cambia el carácter de la solución al mover k:

Otra cosa que resultaba ‘rara’ del comportamiento caótico era que reglas aparentemente muy sencillas (como puede ser elevar al cuadrado y restar 1) daban comportamientos muy complicados. También ocurre al revés, reglas aparentemente complicadas dan comportamiento simple.

Quizá otro día hable del sistema de Lorenz y de su atractor famoso.