Actualmente cuando uno piensa en problemas sin resolver en física piensa en la Teoría del Todo, en el bosón de Higgs o en los límites de validez de la mecánica cuántica. Sin embargo, existen problemas que son fáciles de entender que aún no tienen respuesta. Problemas que sólo involucran a la mecánica de Newton y que todavía no sabemos cómo atacar. Vamos a introducir el que nos ocupa con un experimento que puede ser fácilmente realizado en casa.
Supongamos que tenemos un par de vasos pequeños. Uno está lleno hasta arriba de agua y el otro lo está de vino. El problema es ¿ cómo pasar el agua al vaso en el que está el vino y el vino al vaso en el que está el agua sin utilizar nada más que un carnet de identidad y evitando que se mezclen? Sí, habéis leído bien, no se puede usar ni un tercer vaso ni otro recipiente. Seguid leyendo y trataremos de explicar cómo hacerlo y por qué ocurre así…
Nos referimos al problema de la turbulencia. Ya Richard P. Feynman (un famoso físico del siglo pasado) dejó escrito a sus alumnos en sus Feynman’s lectures
(…) existe un problema físico que es común a muchos campos, que es muy viejo y que no ha sido resuelto. No es el problema de encontrar nuevas partículas fundamentales, sino algo que se viene arrastrando desde hace mucho tiempo (…). Nadie en la física ha sido capaz de analizarlo de forma matemáticamente satisfactoria a pesar de su importancia para las ciencias hermanas. Es el análisis de los fluídos turbulentos. (…) Lo que realmente no podemos hacer es tratar el agua real y húmeda que fluye a través de un tubo.
Hablando claramente, el problema que nos preocupa es el de los remolinos en el agua. Dicho así parece sencillo, lo vemos todos los días al ducharnos; no obstante, las ecuaciones que describen el movimiento (velocidades y aceleraciones) del fluido, que reciben el nombre de ecuaciones de Navier-Stokes, son muy complicadas.
¿Por qué molestarnos con este problema? Si pensamos un poco, nos damos cuenta de lo importante que es entender bien el movimiento de los fluidos. Por citar sólo un ejemplo, una mejor aerodinámica disminuye el consumo de combustible en los coches.
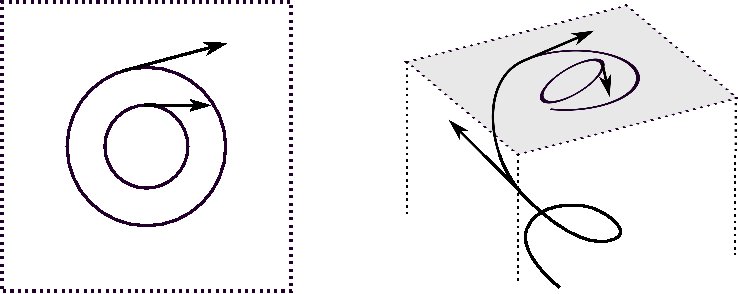
La teoría para el caso en que el fluido se mueve en dos dimensiones es satisfactoria. Pero cuando no nos restringimos a dos dimensiones, nos encontramos con un problema que, de momento, se ha demostrado insalvable. Esto ocurre porque, en tres dimensiones, los remolinos tienen mucho sitio para girar y revolverse.
Así, en dos dimensiones, un remolino sólo puede girar. Lo hará más o menos rápido, pero siempre vendrá descrito por un solo numero, llamado vorticidad. En el caso tridimensional, el fluido puede revolverse, y ese giro vendrá descrito por un vector, esto es, tres números. Esta es la diferencia fundamental: en tres dimensiones, distintas capas bidimensionales pueden mezclarse.
¿Qué tiene que ver la vorticidad con nuestro problema? Para mezclar dos cosas, como un café con leche o un vaso de chocolate caliente, las removemos de una manera parecida a los dibujos anteriores. De modo que, cuando tratamos mezclas, la vorticidad entra en juego.
Entonces, ¿ cu\’al debe ser la estrategia para conseguir cambiar los líquidos de recipiente? Tenemos que conseguir engañar a los líquidos de manera que crean que viven en dos dimensiones.
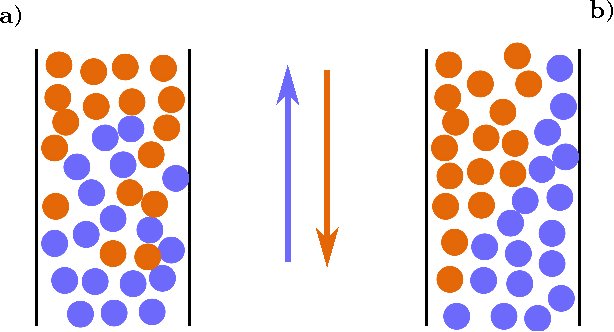
El vino, por ser menos denso que el agua, estando al principio bajo el agua puede “subir”, y el agua “bajar” hacia el recipiente donde estaba el vino. Pero no al revés. Además hemos de evitar los “remolinos” que mezclen ambos fluidos. Esto se consigue preservando las “fronteras” entre partículas del mismo fluido. ¿ Por qué preservando la frontera? Si imaginamos dos grupos de personas andando en sentidos contrarios por una calle estrecha, cada grupo tiene que ir pegado a una de las paredes para no mezclarse. Con los líquidos, esto sería equivalente a que se moviesen en dos dimensiones (por la pared) evitando que se mezclen en la tercera dimensión.
Y ahora, la práctica. Podemos colocar el vaso de agua sobre el de vino utilizando un carné de identidad como dique entre ambos líquidos (quizas derramando unas pocas gotas). Ahora, abrimos una pequeña ranura para que el fluido se mueva en el plano junto a la pared del vaso. Si abrimos una ranura demasiado grande los líquidos se mezclarán. Si lo hemos hecho bien, veremos una lámina de vino subiendo hasta la parte superior del vaso donde antes sólo había agua y una lámina de agua bajando al fondo del del vaso inferior. Sólo queda esperar, pues, esperar a que se cambien de vaso.
Con este “sencillo” problema podemos comprender la relación entre las matemáticas y los problemas de las ciencias naturales: las ciencias obtienen leyes del comportamiento de la naturaleza bajo ciertas condiciones, las matemáticas las formalizan y las ponen en un contexto más amplio, permitiendo realizar predicciones que pueden ser utilizadas por la ciencia o la técnica para su avance. Ciertamente, en nuestro caso, esto nos permite amenizar una fiesta o ganarnos una ronda a la salud de nuestros amigos.
–Nota: Esta entrada la hemos escrito conjuntamente David Paredes Barato y yo mismo.



Pingback: Resumen del Carnaval de Matemáticas Edición 3.1 (actualizándose) | Scientia potentia est
Pingback: ¡A votar! (Carnaval de Matemáticas 3.1) | Scientia potentia est
Pingback: La ecuación de Burgers | Scientia potentia est
Interesante artículo y explicaciones simples y practicas para comprender un tema complejo. Felicitaciones colegas!