Cuántica e incertidumbre (Parte I)

Posted on 19/04/2011 by xhaju

Hoy vamos a hablar, procurando no ser muy rigurosos (aparecen algunas fórmulas pero se pueden saltar), de por qué la mecánica cuántica es necesaria y del principio de incertidumbre de Heisenberg. La entrada la hemos escrito de manera conjunta Rafa y yo mismo.

Werner Heisenberg, uno de los padres de la Mecánica Cuántica

Principios de incertidumbre hay muchos, básicamente no es mas que una desigualdad de cierto tipo, donde un término controla a otro. En el caso concreto que nos atañe afirma que es imposible conocer con precisión la posición y la velocidad de una partícula cuántica (para fijar ideas un electrón). Los físicos (experimentales al menos) razonan diciendo que eso es porque para detectar un electrón hay que golpearlo con un fotón y entonces cambias su velocidad.

Esto nos deja con la duda: ¿habrá algún método que permita conocer las dos cosas?

La respuesta es que no. Y el motivo, enraizado en las matemáticas, tiene que ver con la transformada de Fourier. El ‘teorema’ aquí es que si tienes una función “grande” su transformada de Fourier es “pequeña” y viceversa (se puede intuir usando la desigualdad de Haussdorf-Young por ejemplo.). ¿Cómo afecta esto a nuestro electrón?. Los impacientes estarán pensando que se me está yendo la olla.

Pero comencemos aclarando por qué todas estas cosas tan raras de la cuántica son necesarias: supongamos que tenemos un átomo de hidrógeno (un electrón y un protón), y que tanto nuestro electrón como el núcleo del átomo se comportan como partículas clásicas. Entonces, al tener el núcleo carga eléctrica positiva y nuestro electrón carga eléctrica negativa deberían atraerse por la fuerza coulombiana entre ellos. Cuando un cuerpo con carga se acelera emite radiación electromagnética (véase la fórmula de Larmor [aquí inglés]) perdiendo así energía.

En una dimensión, la posición del electrón, x, oscilaría y caería hacia el origen de coordenadas. Su velocidad, p, también oscilaría y lo llevaría hacia el centro, radiando energía en el proceso.

Según este modelo el electrón se vería atraído irremisiblemente hacia el núcleo y acabaría chocando con éste. Pero esto implicaría ¡que no habría electrones!. En jerga científica diríamos que la materia no sería estable. Puesto que nosotros somos materia y estamos aquí las hipótesis de nuestro modelo no pueden ser correctas.

En otra entrada explicaremos la descripción de los estados en mecánica clásica y cuántica, pero permitidnos ahora que hagamos algunos supuestos. En la mecánica clásica la evolución de un sistema se describe como la trayectoria de un punto en el estado de fases. Sin embargo, en la mecánica cuántica esto no es posible, dado que el estado de un sistema solo puede venir dado como una “probabilidad”, de modo que no existe trayectoria de un solo punto que se adecue a la evolución temporal de un estado. Aquí, pues, la incógnita será una función (con argumentos en el espacio-tiempo y con valores en los complejos) $\Psi (x,y,z,t)$ cuyo módulo al cuadrado (que es un número real) nos dará la densidad de probabilidad de que un sistema se encuentre en un cierto estado.

Esta función, que llamaremos “función de onda”, evoluciona de acuerdo con la ecuación de Schrödinger. Esta es una ecuación en derivadas parciales (EDP) “cualitativamente” hiperbólica (ver la entrada anterior ). Para mayor simplicidad vamos a suponer aquí que no depende del tiempo, con lo que ahora nuestra ecuación de Schrödinger es elíptica y se puede escribir como la función que minimiza un funcional de acción (ya hablamos antes de este concepto) $J(\Psi)= \int |\nabla \Psi(x)|^2 dx +\int V(s)|\Psi(x)|^2 dx$

Si utilizamos, como representación de la función de onda, la base de POSICIONES, la densidad de probabilidad asociada a nuestra función de onda, $\int_A |\Psi(x)|^2dx$ , nos dará la probabilidad de que el sistema (en este caso, nuestro electrón) esté en una zona A del espacio.

Si nos interesa el MOMENTO (i.e. la velocidad), su función de onda es la transformada de Fourier de la función de onda de posiciones, $\hat{\Psi}(p)$ , y esta es la madre del cordero.

En la mecánica clásica la posición y el momento eran independientes. Por eso, podríamos realizar medidas sobre una y otra cantidad sin afectar a la otra.

Ahora, no obstante, tenemos una ligadura: hay una relación que conecta la posición y el momento, y ha de cumplirse. Podemos, pues, escribir nuestro funcional en términos de las dos funciones de onda $J(\Psi,\hat{\Psi})= \int |\hat{ \Psi}(p)|^2|p^2| dp +\int V(s)|\Psi(x)|^2 dx$ .

La formulación del principio de incertidumbre de Heisenberg es, pues, $\int x^2|\Psi(x)|^2 dx \int p^2|\hat{\Psi}(p)|^2 dp=\int |\nabla_x \Psi(x)|^2 dx \int |\nabla_p \hat{\Psi}(p)|^2 dp\geq C$ donde C es cierta constante que podemos escribir explícitamente pero que hacerlo nos da una pereza superlativa por lo que lo dejamos ‘para el lector interesado’ ;). La constante es una ensalada de constante de Planck $\hbar$ , $\pi$ , algún dos… Puede escribirse también involucrando sólo una función de onda de la misma manera que se hace con el funcional.

Hemos dicho que $\Psi(x,t)$ nos da una probabilidad, con función de densidad $|\Psi(x,t)|^2dx$ . Así observamos que en realidad el término $\int x^2|\Psi(x)|^2 dx$ es la varianza de nuestra variable aleatoria $|\Psi(x,t)|^2$ (que asumimos tiene media x=0, es decir, que nuestro electrón está más o menos rondando el origen de coordenadas espaciales).

Entonces si entendemos esas ‘normas’ de los gradientes como los “errores” (utilizaremos esta palabra aquí a modo explicativo, pero hay que ser cautos con la terminología), veremos que un error pequeño en alguna de nuestras mediciones, para fijar ideas, la posición, implica que el error del momento (es decir, de la velocidad) tiene que ser alto para que el producto sea mayor que una constante. Es más: cuanto mejor midamos una (menor error) mayor es el error de la otra. ¡Qué vida más dura la nuestra!

No he hablado nada claro en este último párrafo, y los exigentes se habrán quedado pensando que me explico muy mal (quizá tengan razón). Hemos calculado un par de ejemplos ilustrativos usando python. Hemos supuesto que es unidimensional y que nuestras funciones de onda toman valores en los reales y no en los complejos. No lo hacen, pero sed generosos con nosotros que esto es sólo una afición.

Supongamos que nuestra onda es como la de esta figura

Función de onda con momento definido: seno

Si la funcion de onda es como un seno, la longitud de onda (o el momento) está bien definida.

Entonces por la fórmula de De Broglie, que conecta la visión de partículas con la de ondas, tenemos una velocidad definida (con poco o ningún error), que depende de la longitud de onda (¡otra entrada por hacer!). Esto de nuevo enlaza con nuestra transformada de Fourier, dado que este tipo de transformadas nos llevan desde el espacio de posiciones al espacio de momentos. Sin embargo, no conocemos nada de la posición, pues la probabilidad no se decanta por ninguna zona en particular y salvo puntos donde nunca estarán los electrones por lo demás no podemos decir nada. (Para el lector interesado, decir que esta función de onda no está bien definida en el espacio de posiciones: no es normalizable)

Otro caso interesante es algo así como:

Un paquete gaussiano es una elección "popular" de función de onda porque tiene incertidumbre mínima

En esta segunda imagen tenemos una función tal que al hacer el cuadrado obtenemos una zona que acapara casi toda la probabilidad, un entorno del origen (como la vida misma, unos pocos acaparan casi toda la proba…, digo, billetes). Es decir, casi sin error podemos saber su posición; sin embargo, no podemos usar la fórmula de De Broglie para calcular su velocidad, pues ¿quién me dice su longitud de onda?…

Para ir concluyendo ¿cómo enlaza esto con los gradientes (es decir, las derivadas)?, observamos que una función como la de la figura 1 tiene un gradiente ‘pequeño’, mientras que una función cómo la de la figura 2 tiene un gradiente ‘grande’. Sólo hay que ver que ese pico tiene una derivada bien grande. Así tenemos que entender que los gradientes me dan una idea del error, pero cambiando la variable. Es decir, una gradiente alto en las x me dice un error grande en las p y un error pequeño en las x. Aunque no hemos hablado de ello, esto tiene que ver con la estructura geométrica de las ecuaciones del movimiento Hamiltonianas (ya llegará, ya llegará…).

Es sorprendente (pero usual) cómo la física a veces acaba teniendo que ver con ideas abstractas de las matemáticas (al revés también ocurre).

Hay más que contar, pero se está insinuando una entrada muy larga, así que en la segunda parte de esta entrada escribiremos más acerca de los desarrollos matemáticos de la Transformada de Fourier y de si se puede obtener alguna propiedad física desde las matemáticas.

=======================

Esta entrada es participante en la XVIII Edición del Carnaval de la Física, alojado por “La Aventura , en la mecánica cuántica esto no es posible, de la Ciencia“.

Inferir la Ley: ¿es siquiera posible?

Posted on 01/03/2011 by el guacho

El Viernes pasado estuve en la conferencia “SERIES LÓGICAS Y CRÍMENES EN SERIE” de Guillermo Martínez, el autor de “Crímenes imperceptibles” (que es la novela en la que se basa la película “Los crímenes de Oxford”. La presentadora de la conferencia fue Rosa Montero y estaba organizada por el Instituto de Ciencas Matemáticas (que es donde trabajo).

La presentación del conferenciante no me gustó mucho. Creo que la señora Rosa Montero transmitió una serie de tópicos sobre los matemáticos que se pueden resumir en la siguiente frase, que cito textualmente,

“Tener un amigo matemático es como tener un amigo trapecista: exótico.”

La conferencia en sí no estuvo mal… No eran matemáticas y sospecho que este tipo de charlas divulgativas tienen un efecto contraproducente, pero Guillermo Martínez lo contó muy bien y ameno. En general pienso que este tipo de charlas hace que la gente culta de formación no-matemática piense que nosotros lo que hacemos es…mmm… ¿contar? ¿resolver problemas de lógica como los de los libros de pasatiempos? Y en una ausencia completa de humildad piensan que la matemática es algo completamente inútil. ¡Cómo no va a ser inútil resolver pasatiempos de manera profesional! Creo que toda conferencia divulgativa debería empezar indicando algo así:

“Señores, lo que van a ver aquí está muy alejado del campo en cuestión. Es algo divertido y fácil de entender, no como los problemas reales que tratamos de resolver.”

Vamos ahora al tema de la conferencia en cuestión: las series lógicas. Una serie lógica es una colección de símbolos o números finita y para la que se necesita continuación. Por ejemplo, 2,4,8,16… En la conferencia se nos habló de la falta de unicidad para la continuación. Es decir, que dada una serie la respuesta correcta no es única. En el ejemplo anterior todo el mundo diría que sigue el 32, pero 31 también es una respuesta correcta (se puede razonar, si alguien tiene interés que ponga su duda en los comentarios y la responderé).

Guillermo Martínez usó un argumento basado en interpolación para concluir que dada una colección finita de números hay una manera de razonar que permite continuar la serie con cualquier otro número. La idea es que dada la serie 2,4,8,16, la respuesta puede ser $x$ para cualquier número. Eso es porque podemos construir un polinomio (que se llama polinomio interpolador de Lagrange) de manera que pase por los puntos (1,2), (2,4), (3,8) (4,16) y (5, $x$ ), por lo tanto dicho polinomio es una Ley que concuerda con los experimentos anteriores, pero entre las distintas “Leyes” difieren en el 5º experimento. Ludwig Josef Johann Wittgenstein ya habló de eso en su obra.

Así, dada una colección aparentemente aleatoria de números, podemos construir un polinomio interpolador que nos sirva de Ley y nos “explica” como “se han obtenido”. El tema de lo que significa “aleatorio” surge aquí, pues si dada una colección siempre podemos encontrar una Ley… ¿qué significa una colección de números aleatorios? Por ejemplo, en Matlab tenemos la función rand, que nos da un número entre 0 y 1 “aleatorio”. Claramente estos números no son aleatorios, los genera un ordenador usando una fórmula. Sin embargo usando los criterios existentes (que no nos dicen cuándo una secuencia es aleatoria sino cuándo una secuencia PASA POR aleatoria) son indistinguibles de números verdaderamente aleatorios (los que se sacasen con los ojos vendados de un bombo). Por lo tanto en la práctica nos sirven.

El problema de la inferencia de una Ley dado un número finito de experimentos es irresoluble, ya lo dijo Wittgenstein, sin embargo es lo que hace la física todos los días de manera más que aceptable. Basta con tener una Ley “dinámica”, me explico, si vale la usamos, cuando no valga la cambiamos por una que nos cumpla todos los nuevos experimentos y así vamos tirando para delante. Y he de decir que de manera más que satisfactoria. Por lo tanto, quiero desde aquí tranquilizar a todos los asistentes a la conferencia a los que vi visiblemente sorprendidos, casi en estado de shock. De acuerdo, no podemos saber si la Ley que usamos es la correcta, pero, mientras nos funcione bien ¿qué más nos da? Lo demás son pasatiempos.

Proteinas, ¡dobláos!

Posted on 23/02/2011 by xhaju

El “misterio” del plegamiento de proteinas está más cerca de su resolución: científicos en China han descubierto la ley que relaciona el comportamiento del plegado con la temperatura [1].

Hasta ahora se había pensado que las proteínas, largas cadenas de aminoácidos, se plegaban de modo “mecánico” (clásico), de modo que la proteína tenía que pasar por todos los estados intermedios hasta la forma funcional final. Simulaciones se habían llevado a cabo utilizando modelos clásicos de plegamiento de proteinas.

Las proteinas se pliegan hasta su forma funcional, que es la de mínima energía

No obstante, los posibles disposiciones en que las proteínas se pueden doblar son MUCHAS [imaginémonos de cuantas maneras se puede doblar una cuerda muy larga], y la forma funcional es una determinada de estas disposiciones. En concreto, esta forma funcional sería el mínimo de energía en el plegado de la proteína, y parece ser que este mínimo no depende del modo en que se llega a la forma funcional (clásico o cuántico).

Además, los biólogos tienen datos que avalan que este proceso es muy sensible a la temperatura, y lo extraño es que no sigue la ley de Arrhenius [1](tendría que ser lineal en el logaritmo de la tasa de plegado con la inversa de la temperatura), sino que se comporta de modo no-lineal.

Lo que proponen estos científicos es que las proteínas no se mueven de modo mecánico hasta su forma final, sino que realizan un “salto cuántico” hasta ella. De este modo, al no tener que evaluar todas esas disposiciones, este plegamiento puede ser muy rápido (del orden de nanosegundos).

Utilizando este método, los científicos son capaces de predecir la dependencia de la tasa de plegado con la temperatura y sus resultados se ajustan bastante bien con los datos experimentales [2].

Referencias:

[1] Enlace en inglés, desde el MIT technology review blog: http://www.technologyreview.com/blog/arxiv/26421/?ref=rss

[2] “Ecuación de Arrhenius” en la wikipedia. Nivel básico en español o más completo en inglés.

[3] L. Luo and J. Lu, “Temperature Dependence of Protein Folding Deduced from Quantum Transition”, eprint arXiv:1102.3748 [arxiv]

Introducción al cálculo variacional en la física

Posted on 24/01/2011 by xhaju

Siempre me ha resultado curioso la facultad sorpresiva de la Naturaleza. Nos empeñamos en admirar lo compleja que es en cada detalle. Y después descubrimos que, si miramos desde el punto de vista adecuado, todo es simple. Los científicos nos inventamos leyes (de acuerdo con unas observaciones) para intentar comprender cómo funciona, y al final basta con unos pocos principios fundamentales para derivar el resto.

Al principio estas leyes suelen ser engorrosas, pues de manera experimental intentamos contrastar nuestras observaciones con funciones que se asemejen a nuestros resultados con el fin de poder predecir más fenomenología. Así le ocurrió a Kepler que, habiendo heredado los datos de Tycho Brahe y teniendo observaciones de altísima calidad, enunció las tres leyes que llevan su nombre. Estas leyes requirieron de mucho trabajo experimental y análisis de datos para ser obtenidas y son todo un triunfo de la ciencia. Sin embargo, como en todos los campos científicos, son solo una aproximación de la realidad e introducir perturbaciones (dadas por otros planetas) eran necesarias para poder reproducir con más detalle los resultados.

Más tarde, arduos razonamientos acerca de las observaciones suelen llevar a refinamientos de la teoría. De este modo, Newton propuso la “ley de la gravitación universal” que, aplicada a un sistema simple bajo ciertas suposiciones, ¡daba como resultado las leyes de Kepler!

En el ejemplo anterior, afortunado donde los haya, no he querido entrar en las teorías anteriores de epiciclos y deferentes. Estas “teorías” se ajustaban muy bien a los datos experimentales y por eso tardaron tanto en ser desbancadas. Sin embargo, recientemente se ha demostrado que dado un número suficiente de epiciclos y deferentes, se puede reproducir cualquier órbita, pero esto no nos interesa… lo que queremos es saber cómo son las cosas y, en general, predecir el comportamiento de los sistemas de acuerdo con nuestro conocimiento: si nuestro método puede dar como pronóstico cualquier cosa , la realidad deja de tener sentido y pasa a ser un caso particular, en vez de ser el sujeto central de lo que nos atañe.

Por eso es tan importante la simplicidad. El objetivo de todo científico es poder hacer prediciones sobre el comportamiento de la realidad; si está descrito de manera muy compleja es posible que no estemos teniendo en cuenta los parámetros y simplificaciones adecuados para nuestro sistema en cuestión.

Supongo que algo así deberían tener en la mente los científicos y matemáticos de los siglos XVIII y XIX cuando fundaron lo que se denominó “mecánica analítica”. Para ello, utilizaron el metafísico “principio de mínima acción” que plantea, en palabras de Maupertuis [1] que

“…la Naturaleza siempre actúa de la manera más simple posible para producir sus efectos.”

Y… ¿para qué sirve este principio? Voy a ilustrarlo con un ejemplo de mecánica clásica. Queremos saber qué camino tomará un cuerpo en una cierta situación. Imaginemos que tenemos una cantidad (un funcional, matemáticamente hablando), a la que llamaremos acción, que depende del “camino” que ese cuerpo toma en su movimiento. Esa acción puede ser calculada para cada cualquier camino siempre y cuando tenga una cierta regularidad. Pues bien, el camino real, el que tomará el cuerpo y que podrá ser predicho, es aquel que hace de la acción un mínimo (más rigurosamente, un valor estacionario). Esto es “fácil” de entender:

Si calculamos la acción para todos los caminos, escogemos el camino que tiene la acción más pequeña, esa trayectoria es nuestra solución.

Simple, ¿no?

Muestra del principio de mínima acción en algunos posibles caminos

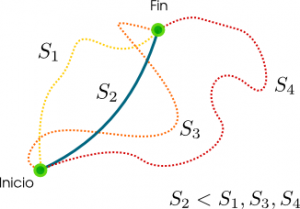
Si a cada posible trayectoria de un cuerpo entre los puntos inicial y final de su trayectoria se le asigna una acción S, la trayectoria real será aquella que tenga la acción menor. Aquí, la segunda trayectoria 2 será la real, por tener la acción menor al resto.

Pensémoslo por un segundo… ¿no es cierto que el número de caminos posibles es infinito? ¡¿Tenemos que calcular la acción para todos los posibles caminos?!

La respuesta es “no”. Hete aquí la belleza de la Naturaleza y del ingenio humano. Matemáticamente es un poco engorroso de explicar, y se necesita alguna fórmula, de modo que dejaré tan engorrosa tarea a Rafa, más versado que yo en estos temas.

Uno de los trabajos de la física es averigüar cuál es la definición correcta de acción que nos da resultados que se correspondan con el comportamiento de la Naturaleza.

Por mi parte, y como estaba planeado, escribiré sobre las dos principales ramas de esta teoría en la física, el método Lagrangiano y Hamiltoniano, utilizando como guía el oscilador armónico. De este modo, comprenderemos un poco mejor las ventajas y desventajas de este método en comparación con la mecánica vectorial de Newton (de la que ya hablamos aquí)

Por último, una reflexión:

Simplicidad no implica que vaya a ser fácil obtener un resultado correcto. Simplicidad implica que puedes contárselo a tu abuela (de una manera más o menos burda).

En estas lineas, Euler dejó escrito [2]:

“Comparados con los métodos de la mecánica tradicional, puede ser que el movimiento sea más dificil de calcular utilizando nuestro nuevo método; sin embargo, parece más fácil de comprender desde primeros principios.”

Referencias:

[1] Maupertuis, Accord de différentes loix de la nature qui avoient jusqu’ici paru incompatibles (1744) (Traducción inglesa, original en francés) Nótese que aplica su sistema a la óptica, como lo hizo antes Fermat.

[2] Euler, Metodus inveniendi. Additamentum II (1744) (traducción inglesa)

[3] Cornelius Lanczos. The variational principles of mechanics (1949)

(Esta entrada es una contribución al XV Carnaval de la Física alojado por Curiosidades de la Microbiología)

El oscilador armónico – Parte I

Posted on 17/12/2010 by xhaju

Hola a todos.
Esta entrada es mi primera contribución al blog, y siendo físico me gustaría comenzar con el que es el ladrillo de la física: el oscilador armónico.
El nombre, que nos da una idea de a qué nos estamos enfrentando, indica el movimiento de algo que se repite en el espacio y en el tiempo. Matemáticamente, siendo más estrictos, un movimiento armónico sería el descrito por una función “seno” o “coseno” . La palabra “armónico”, procedente del griego, nos da la idea de una conveniente proporcion y correspondencia entre unas y otras cosas. El concepto aparece en música, como la unión de sonidos acordes, y Kepler (amante de la música y con su mente puesta en ella) lo utilizaba como expresión de belleza y unión entre las matemáticas y el movimiento celeste. [Vease “La armonía de los mundos“] Continue reading →

¿Podemos ir hacia atrás (matemáticamente) en el tiempo?

Posted on 13/12/2010 by el guacho

Me comentó David que sería interesante que explicase un poquito de lo que significa la reversibilidad temporal desde el punto de vista de las ecuaciones en derivadas parciales (EDPs de ahora en adelante). Es decir, sin mencionar nada de entropías. Este es un tema muy interesante e importante aunque a primera vista parezca una tontería. Lo hemos puesto como una serie de dos entradas. La primera (esta que estás leyendo) presentará las EDPs más fáciles y estudiará sus propiedades de cara a la reversibilidad temporal. En la segunda veremos la derivación de unos modelos más complicados y trataremos de entender dónde aparece la irreversibilidad temporal. Lo cierto es que en cierto modo es llamativo, pues las leyes de Newton son reversibles en tiempo y muchas (casi todas) de las ecuaciones de las que hablaremos surgen de ellas.

Viendo qué ocurre:
Para entender qué quiere decir y qué implica la reversibilidad (o irreversibilidad) temporal hemos de comprender primero los ejemplos más básicos de EDPs. Como dato para los técnicos supondré que todos los problemas están puestos para $(t,x)\in [0,T]\times\mathbb{R}$ . Inmerso en el texto hay imágenes .jpg, imágenes animadas .gif (pinchad en ellas para que empiecen a moverse) y código Matlab (¡usadlo si podéis!).

La ecuación del transporte:

Comenzaremos con la ecuación del transporte unidimensional con coeficientes constantes. Esta es la EDP más sencilla que podemos poner.

$\partial_t u + c \partial_x u=0, u(0,x)=f(x).$

Supondremos que $f$ es una función derivable con derivada continua una vez. La solución de esta ecuación es $u(t,x)=f(x-ct)$ (¡comprobadlo!). Esta ecuación se llama ‘del transporte’ porque lo que hace es eso ‘mueve’ nuestra distribución inicial $f$ . Si queremos cambiar el sentido del tiempo hemos de hacer el cambio $t$ por $-t$ . Entonces la nueva ecuación es

$-\partial_t u + c \partial_x u=0, u(0,x)=f(x).$

Observamos que el cambiar el tiempo de sentido es equivalente a cambiar el signo de $c$ . Si utilizamos el código que propongo con varios valores de $c$ observamos que este parámetro es una velocidad. Por lo tanto, parece natural que cambiar el sentido del tiempo cambie el sentido del movimiento. Es decir, que si para $c>0$ íbamos a la derecha, para tiempos negativos (o equivalentemente $-c$ ) tenemos que ir a la izquierda. Concluímos así que la ecuación del transporte es reversible en tiempo y que la reversibilidad es muy natural si partimos del proceso físico que se modela con esta ecuación.

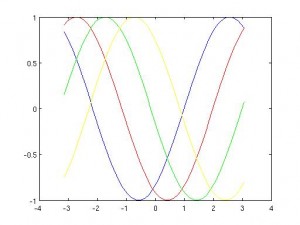
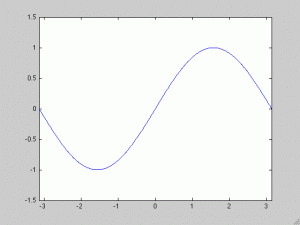
Otra consecuencia, ésta mucho más sutil, de la reversibilidad temporal es que nuestra solución NUNCA va a ser mejor que nuestro dato inicial $f$ . Esto es obvio en este caso porque tenemos una solución explícita, pero es cierto en general. Si $u$ tuviese más derivadas que $f$ entonces dando la vuelta al tiempo tendríamos una contradicción.

function [u,x,t]=transporte(dx,dt,f,c)
%%
%Funcion que me aproxima la solucion exacta (conocida) de la
%ecuacion del transporte u_t+cu_x=0 con dato inicial
% u(0,x)=f(x), paso espacial dx y paso temporal dt.
%f sera una funcion
% Rafael Granero Belinchon
%%

%Definicion de parametros:
T=10; %El tiempo final
t=0:dt:T; %el vector de tiempos
x=-pi:dx:pi; %el vector de espacio donde queremos
%nuestra aproximacion. No necesitamos condiciones de borde ¿por que?
u=zeros(length(x),length(t));
F=feval(f,x);

%Calculo de la solucion:
%La solucion del problema anterior es u(x,t)=f(x-ct)
u(:,1)=F;
for j=2:length(t)
u(:,j)=feval(f,x-c*t(j));
plot(x,u(:,j-1));%Representacion de los resultados
drawnow
end

function f=prueba(x)
f=sin(x);

La ecuación de ondas:

La siguiente ecuación es el paradigma de ecuación hiperbólica. Me refiero a la ecuación de ondas. Viendo el nombre está claro qué proceso físico quiere describir ¿no?.

Esta ecuación se escribe

$\partial_t ^2 u= c^2\partial_x^2 u, u(0,x)=f(x), \partial _t(0,x)=g(x).$

Visualmente parece mucho más complicada que la ecuación del transporte… sin embargo en realidad es igual (al menos en un cierto sentido). Vamos a escribirla como un sistema. Para ello definimos el sistema

$\partial_t u=c\partial_x v, \partial_t v=c\partial_x u.$

Si ahora derivamos en tiempo la ecuación para $\partial_t u$ y utilizamos la segunda ecuación obtenemos

$\partial_t^2 u=c\partial_x \partial_tv=c^2\partial_x ^2 u.$

Es decir, que la ecuación de ondas no es más que dos transportes acoplados. Sin embargo todavía podemos hacerlo mejor. Podemos darnos cuenta de que el operador diferencial se puede escribir como

$\partial_t^2-c^2\partial_x^2=(\partial_t + c\partial_x)(\partial_t-c\partial x),$

y por lo tanto si tenemos $u=u_1+u_2$ con

$\partial_t u_1 + c\partial_x u_1=0; \partial_t u_2 - c\partial_x u_2=0$

tenemos una solución de la ecuación original. Concluímos que, como la ecuación del transporte era reversible, la ecuación de ondas, que se puede escribir como un par de ecuaciones del transporte debe ser reversible también.

La ecuación del calor:

Esta ecuación es parabólica. Se escribe

$\partial_t u= \partial_x^2 u, u(0,x)=f(x).$

Visualmente parece estar a medio camino entre la ecuación del transporte y la ecuación de ondas, sin embargo su comportamiento en radicalmente distinto. Para convencernos de ello podemos ‘jugar’ un poco con el código Matlab que adjunto. Los datos iniciales por defecto son los mismos, pero os animo a cambiarlos.

function [u,x,t,mx]=heatff(N,dt,K)
%%
%Funcion que me aproxima la solucion de la
%ecuacion del calor con dato inicial seno
%con condiciones periodicas (para usar FFT)
%N es el numero de nodos espaciales que se quieren
%usar. dt es el paso temporal que se quiere.
%K es la constante de difusion.
%Devuelve el espacio, el tiempo, la aproximacion de
%la solucion y el maximo de dicha solucion en cada tiempo
%Rafael Granero Belinchon
%%
T=5;%Tiempo final
dx=2*pi/(N-1);
x=-pi:dx:pi;%Espacio
t=0:dt:T;%Tiempo
uo=sin(x);%dato inicial
for k=1:N/2 %Operador laplaciano en espacio de fourier
L(k)=(k-1)*(k-1);
L(k+N/2)=(N/2-k+1)*(N/2-k+1);
end
L=K*L;
u(:,1)=uo’;
mx(1)=max(uo);
for l=1:length(t)
u(:,l+1)=ifft(exp(-L*dt*l).*fft(uo))’;%solucion
mx(l+1)=max(u(:,l+1));%Evolucion del maximo
plot(x,u(:,l));axis([-pi,pi,-1,1]);%Representacion de los resultados
drawnow
end
end

Para estudiar esta ecuación vamos a utilizar la transformada de Fourier. Para la transformada de Fourier de $u(x)$ usaremos la notación $\hat{u}(k)$ . Así si transformamos la ecuación en espacio obtenemos las ecuaciones diferenciales ordinarias (EDOs a partir de ahora) indexadas en la longitud de onda $k$ siguientes

$\frac{d}{dt}\hat{u}(t,k)=-k^2\hat{u}(t,k), \hat{u}(0,k)=\hat{f}(k).$

Esta ecuación la podemos resolver explícitamente

$\hat{u}(t,k)=e^{-k^2t}\hat{f}(k).$

Observemos ahora qué quiere decir el cambio del sentido del tiempo. De nuevo hagamos el cambio $t$ por $-t$ . La ecuación nos queda

$\partial_t u= -\partial_x^2 u, u(0,x)=f(x).$

No se ve nada claro, sin embargo, si buscamos los efectos del cambio en la solución explícita tenemos

$\hat{u}(t,k)=e^{k^2t}\hat{f}(k),$

de manera que cuando invirtamos la transformada de Fourier estamos calculando una convolución con una función que no está acotada, ni tiene ninguna potencia integrable… Vamos, que nuestra solución (que existe explícitamente) no está en ningún espacio razonable ni con propiedades físicas razonables. Por ejemplo, si $u$ es la temperatura, entonces su integral (que es el calor) debe ser finita. Pues si damos la vuelta al tiempo obtenemos calor infinito para cualquier tiempo. Concluímos que la ecuación del calor NO es reversible en tiempo.

Una propiedad que a veces se da en las ecuaciones irreversibles y que es bien interesante es el ‘efecto regularizante’. Es decir, tu dato inicial $f$ es continuo (por ejemplo), pero tu solución $u$ es infinitamente derivable para todo tiempo (positivo). Como ya hemos mencionado antes, este comportamiento difiere del de las ecuaciones hiperbólicas usuales. La prueba de esto se puede hacer sin más que multiplicar por $u$ e integrar por partes en espacio (¡comprobadlo!). Después basta observar que la ecuación es invariante por derivación tanto en tiempo como en espacio (¡Concluid el argumento!).

Vistos estos 3 ejemplos parece que hay una relación entre la ‘simetría’ del problema y su reversibilidad temporal. Quiero decir que, al menos de momento, las ecuaciones que tienen el mismo número de derivadas temporales que espaciales han resultado ser reversibles, mientras que las que no las tienen son irreversibles.

Otra cosa que se nos puede ocurrir es que las ecuaciones reversibles sean las que ‘no tiendan a nada’. Así vemos que la ecuación del calor tiende a ser idénticamente cero (necesita tiempo infinto para llegar a serlo) mientras que la ecuación del transporte sólo se movía por el espacio.

Veamos otro ejemplo:

La ecuación de Schrödinger:

Esta ecuación, clave en mecánica cuántica, se escribe

$\partial _t u= i\partial_x^2 u, u(0,x)=f(x).$

Si repetimos el análisis que hicimos para la ecuación del calor obtenemos que la solución es

$\hat{u}(t,k)=e^{-ik^2t}\hat{f}(k),$

que tiene un comportamiento oscilatorio. Por lo tanto, pese a tener una derivada en tiempo y dos en espacio se parece más a una ecuación de ondas que a una ecuación del calor. Observamos que el hecho de que aparezca la unidad imaginaria hace que $u$ no sea real, sino compleja. Por lo tanto tiene una función conjugada. Si ahora cambiamos el sentido del tiempo observamos que para la función conjugada $\bar{u}$ la ecuación es la misma. Por lo tanto si $u$ es nuestra solución con el tiempo hacia delante, $\bar{u}$ es una solución con el tiempo hacia atrás. Por lo tanto la ecuación de Schrödinger es reversible. Este ejemplo desmonta la hipótesis de que als reversibles debían tener el mismo número de derivadas en espacio y en tiempo.

function [u,x,t,L2,mx]=schrodinger(N,dt)
%%
%Funcion que me aproxima la solucion de la
%ecuacion de schrodinger con dato inicial seno
%con condiciones periodicas (para usar FFT)
%N es el numero de nodos espaciales que se quieren
%usar. dt es el paso temporal que se quiere.
%Devuelve el espacio, el tiempo, la aproximacion de
%la solucion, la norma L^2 de dicha solucion en cada tiempo
%y el maximo de la solucion en todo tiempo.
%Rafael Granero Belinchon
%%
T=5;%Tiempo final
dx=2*pi/(N-1);
x=-pi:dx:pi;%Espacio
t=0:dt:T;%Tiempo
uo=sin(x);%dato inicial
for k=1:N/2 %Operador laplaciano en espacio de fourier
L(k)=(k-1)*(k-1);
L(k+N/2)=(N/2-k+1)*(N/2-k+1);
end
L=i*L;
u(:,1)=uo’;
L2(1)=norm(uo)*dx;
mx(1)=max(abs (uo));
for l=1:length(t)
u(:,l+1)=ifft(exp(-L*dt*l).*fft(uo))’;%solucion
L2(l+1)=norm(u(:,l+1))*dx;%Evolucion de la norma L^2
mx(l+1)=max(abs(u(:,l+1)));%Evolución del máximo
plot(x,real(u(:,l)));axis([-pi,pi,-1,1]);%Representacion de los resultados
drawnow
end
end

Como dato anécdotico de esta ecuación hacemos notar que no puede reflejar efectos relativistas (¿por qué?).

En la próxima entrada, enlazando con esta, trataré la derivación desde la mecánica hamiltoniana de los modelos que se utilizan en mecánica de fluidos y trataré de explicar dónde aparece la irreversibilidad en el proceso. Sin embargo, esto es algo que no está ‘completamente entendido’ todavía.

Scientia potentia est

Category Archives: Física