Car Dashboard by Albert Lynn(CC BY-NC-ND 2.0)

Respuesta corta: Ajustando modelos de eficiencia a datos de consumo

Para la respuesta larga debería explicar que es eso de “ajustar modelos a datos”. Típicamente en física y en ingeniería uno cuenta con una serie de datos (en nuestro caso, cuántos litros hemos utilizado en una cierta distancia) y desarrolla un modelo teórico que pueda describir las observaciones que ya están hechas y predecir resultados en situaciones en las que todavía no tenemos datos. Por ejemplo, cuando uno va en un coche que tiene esta opción, uno no ha recorrido todavía la distancia que esta marcada y, sin embargo, el coche es capaz de predecir cuánta distancia podrá hacer con el combustible que le queda.

Un modelo es una manera simplificada de describir la realidad.  En el caso del consumo de combustible, el modelo más sencillo tiene las siguientes propiedades intuitivas:

• si tengo que recorrer el doble (o triple) de la distancia, necesitaré el doble (o el triple) de combustible
• si he gastado, digamos, 10 litros en 70km, y 2.5 litros en 12.5km, aproximadamente gastaré 10+2.5=12.5 litros en 70+12.5=82.5km

Matemáticamente, esto lo expresamos con una función lineal:

cantidad de combustible usado [litro] = consumo[ l/km] *distancia recorrida [ km ]

distancia recorrida [ km ]  = eficiencia[ km/l] *cantidad de combustible usado [litro]

o, lo que es lo mismo, , donde representa la distancia recorrida, representa el consumo, y $V$ representa el volumen de combustible usado. Si el consumo es mayor, un coche usará más combustible para la misma distancia recorrida.

Lo que hace el ordenador de abordo para predecir la distancia es estimar cual es la eficiencia del coche, y con ella predecir la distancia que podría recorrer. Por ejemplo, si la eficiencia fuese 25km/l y le quedasen en el depósito 2 litros, el coche podría recorrer cerca de 50km (¡pero sería mejor encontrar una gasolinera antes, por si acaso!).

Estimando la eficiencia

Para estimar la eficiencia, el ordenador de abordo del coche puede hacer muchas cosas diferentes. Nosotros vamos a suponer que va adquiriendo datos de distancia recorrida y combustible usado conforme va circulando (como hacen muchos coches a día de hoy). Así, en nuestro coche de ejemplo, vamos a obtener 5 medidas de combustible a diferentes distancias, y las vamos a representar en el siguiente gráfico.

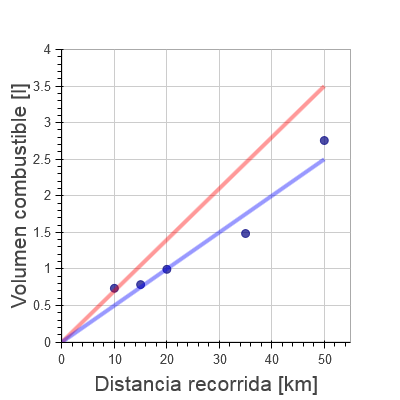
Las dos rectas representan dos eficiencias diferentes. La azul se parece más a la eficiencia “real” y, por lo tanto, es una mejor aproximación.

Si el mundo fuese ideal y maravilloso, todas esos puntos (medidas) estarían encima de una linea recta que, además, pasaría por 0; sin embargo, como ya hemos visto anteriormente, toda medida lleva asociada un error, lo que nos impide obtener un valor preciso o exacto de las cantidades que hemos medido.

Recordemos que nuestro objetivo es estimar la eficiencia; esto es, queremos obtener la pendiente de la recta que pasa más cerca de todos los puntos. En el gráfico de arriba, vemos que una de las rectas (la azul) pasa más cerca de todos los puntos que la otra (roja), así que uno intuitivamente dice que la recta azul “se ajusta mejor” que la roja. Pero, ¿hay alguna manera de obtener la recta que mejor se ajusta a los datos? Pues claro, si no no estaríamos escribiendo esta entrada 😀

Antes de ponernos con un poco de matemáticas ligeras, aquí hay un gráfico interactivo que te permite comparar cómo de buena es la estimación “a ojímetro” de la estimación que vamos a obtener más tarde. Puedes cambiar el valor de la pendiente utilizando el deslizador que hay bajo la figura. Puedes intentar encontrar un valor de la pendiente que mejor describe la eficiencia de nuestro coche:

Descripción matemática sencilla

Como hemos dicho, hay un número infinito de rectas que podrían describir nuestros datos (pensemos en cualquier valor para ), pero obviamente algunos se acercan más a los datos que otros. Para estimar la eficiencia con estos datos, realizamos un ajuste con el modelo lineal que hemos visto más arriba. Si la función que queremos ajustar es (como hemos visto arriba, es el volumen de combustible, es la distancia y es el parámetro de nuestra función- el consumo), lo que tenemos que hacer para obtener el mejor parámetro sería minimizar la “distancia” de esa recta a los datos. La distancia de cada dato a la recta viene dado por . Para minimizar la distancia de la recta a TODOS los datos, podemos intentar minimizar la SUMA de esas distancias. Llamamos “chi-cuadrado” a esa suma:

De modo que encontrando el valor de que hacer el chi-cuadrado más pequeño posible estaríamos obteniendo la recta que minimiza la distancia a los puntos experimentales. El parametro sería entonces nuestra mejor estimación para el consumo de combustible. Si vuelves a mirar el gráfico de arriba, la “mejor” recta sería la que tiene un chi^2 más pequeño; si la recta que has escogido “a ojímetro” es la que minimiza el chi-cuadrado, ¡enhorabuena!

Ese problema de cómo minimizar la distancia de la recta a los puntos se puede atacar de muchas maneras (probando combinaciones al azar, cambiando parámetros de modo secuencial para ir minimizando poco a poco,… ), y sería un tema del que hablar largo y tendido, pero no es el propósito de esta entrada

Colofón:

En esta entrada hemos considerado el modelo más sencillo de todos (una linea recta que pasa por cero). Obtener una estimación no quiere decir que el valor real de la distancia que podemos recorrer sea el valor estimado, solo quiere decir que “si nuestro coche funcionase de esta manera (como dice el modelo) entonces lo más probable es que el valor de eficiencia sea el valor estimado”.

He remarcado lo de “si nuestro coche funcionase de esta manera” porque es la clave del asunto: ¡nada nos garantiza que el coche funciona así! Dependiendo de cuán bueno sea nuestro modelo (y aquí quiero decir, que nuestro modelo describa adecuadamente la realidad), nuestra estimación será más acertada. Usualmente, los modelos de consumo de los automóbiles son más complicados porque dependen de las revoluciones a que va el motor, la velocidad del coche (a más velocidad, más fricción, y por lo tanto más consumo), etc.

Saber si tu modelo es bueno o no es un problema interesante, pero esa es otra historia y deberá ser contada en otro momento.