Como físico experimental, una de las tareas que tengo que hacer día sí, día también, es análisis de datos. Y a menos que sea una cuenta corta (multiplicación, división, …), usualmente uno utiliza el ordenador para esta tarea.
Hace poco escribí un programita en Python para obtener perfiles de linea – esto es, secciones – de una imágen. Como me parece un programa simple y bastante útil quería compartirlo con el resto del mundo.
Peeeero, además de escribiros el código (que está al final), quería comentar de pasada el por qué y el cómo se representan imágenes.
En ocasiones, los datos que adquirimos en un experimento toman forma de “imágenes” que uno tiene que analizar. Una imagen no es nada más que una colección de números asociados a una matriz en dos dimensiones. Por ejemplo, si el dominio es rectangular, una matriz de NxM elementos puede contener una imagen (pensad en los dos numeritos que dan la resolución en el monitor)
Por ejemplo, esta matriz
se puede representar como esta imagen
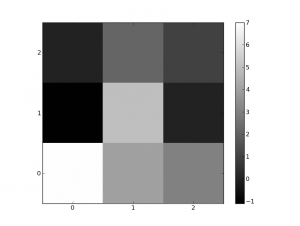
Imagen de la matriz anterior. El color de cada recuadro nos indíca qué número hay en cada posición. La barra de color de la derecha nos sirve como referencia
Cada uno de los elementos de la matriz es un número real, así que podemos representar cada elemento en una escala del blanco (el mayor) al negro (el menor).
Usualmente, imágenes más complejas requieren de 3 de estas matrices para conseguir todos los colores (por ejemplo, el modelo RGB hace uso del rojo, el verde y el azul, con sus siglas en inglés). Pero aunque nosotros nos limitaremos a una sola de ellas, podemos hacer las imágenes un poco más coloridas “mapeando” esa escala de blanco a negro en una escala de colores, usando lo que se llama un LUT (o “look-up-table”).
Ya sea en busca de patrones o para hacer un análisis estadístico de los datos de una matriz, si uno tiene una colección de números reales en “dos dimensiones” pueden ser representados como una imagen (podéis echar un ojo en la wikpedia para más información sobre los gráficos de funciones)
Existen numerosas soluciones comerciales para analizar imágenes, siendo algunas de las más comunes MATLAB, Mathematica, o IDL. No obstante, prácticamente cualquier tarea que se quiera llevar a cabo en un ordenador puede ser realizada mediante software libre.*
Y, en nuestro caso, como nada más que se trata de analizar una “matriz bidimensional”, lo podemos hacer directamente utilizando operaciones básicas.
En el caso que me trae aquí, yo tengo una imagen (una matriz) un poco más grande (1280×1024) obtenida en un interferómetro Mach-Zehnder:

La imagen original solo da información sobre la intensidad en cada punto del sensor. Para obtener esta imagen se ha rotado ligeramente uno de los brazos (moviendo uno de los beamsplitters).
El interferómetro superpone dos campos vectoriales (en este caso, luz en el infrarrojo cercano) y obtiene la diferencia entre ellos. Usualmente, esta diferencia dependerá de la fase que haya entre ambos campos y el solapamiento espacial. La fase de un campo a esa longitud de onda es del orden de los centenares de nanómetros o los micrómetros. Como nuestro instrumento es sensible a cambios en fracciones de esa longitud de onda (la fase entre ambos campos), este interferómetro nos permite, entre otras cosas, medir distancias en ese orden de magnitud (!)
Personalmente, la cantidad que me interesa conocer es la visibilidad de las franjas.
La visibilidad de las franjas se define como
Donde es la intensidad máxima de la envolvente y
el mínimo.
La visibilidad de las franjas depende crucialmente en el solapamiento espacial: a mayor visibilidad mejor el solapamiento espacial es y mejor podré discernir la fase. Si os interesa, un día puedo explicar como funciona este interferómetro, pero “esta es otra historia y deberá ser contada en otro momento”.
¿Cómo medimos la visibilidad en la imagen? Si tenemos la imagen “tal cual” es muy dificil de ver. Sería mucho más fácil si pudiésemos cortar la imagen en vertical y tomasemos una “rebanada” de la imagen para analizarla. Pues bien, eso es tán simple como seleccionar la columna de nuestra matriz que queremos observar y “pintarla”.
Y es ESTO, exactamente, lo que hace el programita que he escrito. Toma un punto y nos muestra las secciónes horizontal y vertical de la imagen que pasan por el punto que seleccionamos usando el ratón. Si lo aplicamos a la imagen que teníamos previamente, obtenemos
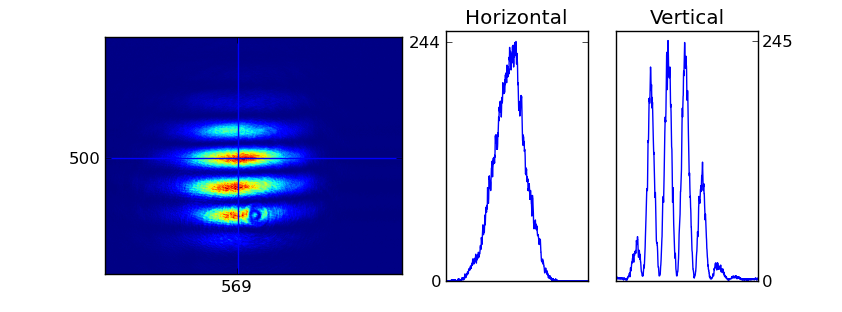
El programa nos muestra de manera concisa los perfiles de linea horizontal y vertical que pasan por un punto. El punto se puede seleccionar con el ratón y se actualiza con cada click.
A juzgar por la imagen, podemos comprobar que en el interferómetro alcanzamos una visibilidad cercana al 95%.
Con esto termina la excursión que he dado para llevarnos al programita en sí, que está adjunto detrás de una nota. ¡Espero le podáis dar buen uso!
¡Ah! ¡Se me olvidaba! Esta entrada participa en el XXXI Carnaval de la física que, en esta ocasión, está organizado por Imperio de la Ciencia.
P.D.: Para poder hacer uso del programa necesitaréis Python, Scipy y Matplotlib
*Nota: El “contra” del software libre es la cantidad de tiempo que tienes que tener para hacer funcionar ciertas cosas. No obstante, si tienes ese tiempo, se aprende mucho más cacharreando con software libre que pulsando teclas como un mono en una solución comercial.
----
''' Analyze the pictures taken by the CMOS sensor.
It plots the picture and the horizontal and vertical profiles
at a given point.
The point can be selected using the mouse by clicking on the
apropriate point.
By default, take the pixel in the midle of the picture and put the
vertical and horizontal traces on the plots.
By David Paredes, 18-V-12
'''
import scipy as sp
import matplotlib.pyplot as plt
from matplotlib import colors
from matplotlib.image import imread
from mpl_toolkits.axes_grid1 import ImageGrid
filename = 'fringes1.bmp' #Aqui va el nombre del archivo que queráis.
#Read the figure
data = imread(filename)
#Obtain the position of the pixel with the maximum value
maxrows = sp.argmax(data,axis=0)
maxrowsVal = data
########## BEGIN FIGURE #########
plt.ion()
fig = plt.figure(figsize=(8.3,3))
# Page width is 8.3 inches
# Create three plots: Picture, and horizontal and vertical profiles
ax1 = fig.add_subplot(121)
ax2 = fig.add_subplot(143)
ax3 = fig.add_subplot(144)
# Given that the two figures on the right are very
# close, we set the labels on the rightmost one
# to the right
ax3.yaxis.set_ticks_position('right')
# If the limits of the y axis are not set, the first point will determine
# the span of it
ax2.set_ylim((0,255))
ax3.set_ylim((0,255))
# Prepare the cross to be updated later
vlin = ax1.axvline(x=data.shape[1]/2)
hlin = ax1.axhline(y=data.shape[0]/2)
#Prepare the plots to be updated later. The generic first point is the central point in the image
imag = ax1.imshow(data,norm=colors.Normalize(vmin=0,vmax=254,clip=True),origin='lower')
row, = ax2.plot(data[data.shape[0]/2,:])
column, = ax3.plot(data[:,data.shape[1]/2])
# Format the axis
ax1.set_yticks([data.shape[0]/2])
ax1.set_xticks([data.shape[1]/2])
ax2.set_yticks([0, max(data[data.shape[0]/2,:]) ])
ax2.set_title('Horizontal')
ax2.set_xlim((0,data.shape[1]))
ax2.set_xticks([])
ax3.set_yticks([0, max(data[:,data.shape[1]/2]) ])
ax3.set_title('Vertical')
ax3.set_xlim((0,data.shape[0]))
ax3.set_xticks([])
#### EVENT HANDLING ######
# We can define a function to work in the event of a click
# In our case, the "click" will update the point at which the profiles
# are taken.
# It is defined after the window is created to avoid having to refer to the
# individual properties. This saves time (knowing the references to vlin, hlin, row, column,...
def onclick(event):
print 'xdata=%f, ydata=%f '%(
event.xdata, event.ydata)
if event.inaxes == ax1:
vlin.set_xdata(x=[event.xdata,event.xdata]) #Update vertical line
hlin.set_ydata(y=[event.ydata,event.ydata]) #Update horizontal line
ax1.set_yticks( [int(event.ydata)])
ax1.set_xticks([int(event.xdata)])
row.set_ydata(data[int(event.ydata),:]) #Update row data
ax2.set_yticks([0, max(data[int(event.ydata),:]) ])
column.set_ydata(data[:,int(event.xdata)]) #Update column data
ax3.set_yticks([0, max(data[:,int(event.xdata)]) ])
plt.draw() #Update!
# This is the part that makes the event handling work:
cid = fig.canvas.mpl_connect('button_press_event', onclick)
plt.show()

Pingback: Resumen del XXXI Carnaval de la Física | Imperio de la Ciencia
Disculpa, si yo deseo obtener o extraer los datos de una imagen en forma de arreglos con python , no se si conozcas algun script, ya que trabajo con opencv y python para detectar fuego y requiero hacer una base de datos
Disculpa, si yo deseo obtener o extraer los datos de una imagen en forma de arreglos con python , no se si conozcas algun script, ya que trabajo con opencv y python para detectar fuego y requiero hacer una base de datos
Hola Jesús.
Hay varias alternativas, pero quizás la más simple (si tienes scipy o matplotlib) sea la función imread (puedes encontrarla en matplotlib.pyplot.imread o en scipy, scipy.misc.imread). Te aconsejaría leer la documentación para saber cómo funcionan.
Además, buscando en google puedes encontrar otras alternativas:
http://lmgtfy.com/?q=leer+imagenes+python
Si imread no te funcionase, házmelo saber
Hola! Una Pregunta, qué puedo hacer si mi espectro de potencias está rotado, es decir, las líneas no son horizontales como en tu caso.
Saludos!
Voy a suponer que lo que quieres es obtener un perfil de linea donde las lineas no son horizontales o verticales.
Googleando un poco he encontrado esta respuesta (en inglés)
http://stackoverflow.com/questions/7878398/how-to-extract-an-arbitrary-line-of-values-from-a-numpy-array
¿Es esto lo que buscas?
¡Excelente! Muchas gracias, tu programa es fantástico porque te permite definir el punto manualmente.
Saludos!